Сортирующие сети для квадратичных сортировок — различия между версиями
System29a (обсуждение | вклад) (→Сортировка пузырьком) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 33 промежуточные версии 9 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | Рассмотрим модели [[Сортирующие сети|сортирующих сетей]] для квадратичных сортировок. | |
| − | |||
| − | Рассмотрим модели сортирующих сетей для квадратичных сортировок. | ||
== Сортирующие сети с последовательной сортировкой == | == Сортирующие сети с последовательной сортировкой == | ||
На один слой будем устанавливать только один компаратор. Все последующие сети получаются простым моделированием соответствующих сортировок. | На один слой будем устанавливать только один компаратор. Все последующие сети получаются простым моделированием соответствующих сортировок. | ||
| + | {| cellpadding="10" | ||
| + | | '''[[Сортировка пузырьком]]''' || '''[[Сортировка вставками]]''' || '''[[Сортировка выбором]]''' | ||
| + | |- | ||
| + | | [[Файл:Bubblesort.png]] || [[Файл:Insertsort.png]] || [[Файл:Choosesort.png]] | ||
| + | |} | ||
| + | |||
| + | == Сортирующие сети с параллельной сортировкой == | ||
| − | + | На один слой устанавливается несколько компараторов. | |
| − | + | === Сортировка пузырьком и вставками === | |
| − | + | Заметим, что если сжать последовательные сортирующие сети пузырьком и вставками, то результат будет одним и тем же. Это видно из симметрии расположения компараторов на картинках выше. | |
| + | {{ | ||
| + | Утверждение | ||
| + | |statement= | ||
| + | В результирующей сети будет <tex>(2n - 3)</tex> слоев, где <tex>n</tex> — количество входов. | ||
| + | |proof= | ||
| + | Докажем данное утверждение по принципу математической индукции. | ||
| − | + | '''База индукции''': | |
| − | = | + | При <tex> n = 2 </tex>. В сети всего два входа, на которых располагается один компаратор, тем самым наше предположение выполняется. |
| − | + | '''Шаг индукции''': | |
| − | = | + | Пусть <tex> S(n) = 2n - 3 </tex> — количество слоев в сети сортировки. |
| − | + | При переходе от сортирующей сети с <tex>n</tex> входами к сети с <tex>n + 1</tex> входами, добавляем <tex> n </tex> дополнительных компараторов (<tex>[1:2],[2:3]\dots[n:n + 1]</tex> или <tex>[n + 1:n],[n:n + 1]\dots[1:2]</tex>, т.к. возможны две стратегии добавления; отсюда, кстати, тоже видна эквивалентность схем для обоих сортировок). Будем также поддерживать сортирующую сеть в виде "треугольной" сети. Таким образом компараторы <tex>[i:i+1],\ i \geqslant 3</tex> можно расположить в существующих слоях над самым верхним компаратором в соответствующем слое. То есть в сети с <tex> n </tex> входами был слой с единственным компаратором <tex>[1:2]</tex>, поэтому над ним можно разместить компаратор <tex>[3 : 4]</tex>, на <tex>[2:3]</tex> {{---}} <tex>[4:5]</tex>. Затем на следующем слое будет уже два компаратора: <tex>[3 : 4]</tex> над <tex>[1:2]</tex>, поэтому сверху можно добавить <tex> [5: 6]</tex>. В общем виде, на слое с номером <tex> k \geqslant 0 </tex> с конца (до середины треугольника), будет <tex>\left\lfloor\dfrac{k}{2}\right\rfloor + 1</tex> компараторов, последним из которых является <tex>[k + 1 : k + 2]</tex>, следовательно, на этот слой можно добавить компаратор | |
| + | <tex>[k + 3 : k + 4]</tex>. | ||
| − | + | Значит, новые слои создадутся лишь благодаря компаратором <tex>[1:2]</tex> и <tex>[2:3]</tex>, поэтому число слоёв в новой сети составит <tex>S(n+1) = 2n - 3 + 1 = 2n - 1 = 2(n + 1) - 3</tex>, что удовлетворяет нашему соотношению. | |
| − | + | }} | |
| − | + | Сортирующая сеть для <tex> n = 6 </tex>: | |
| − | |||
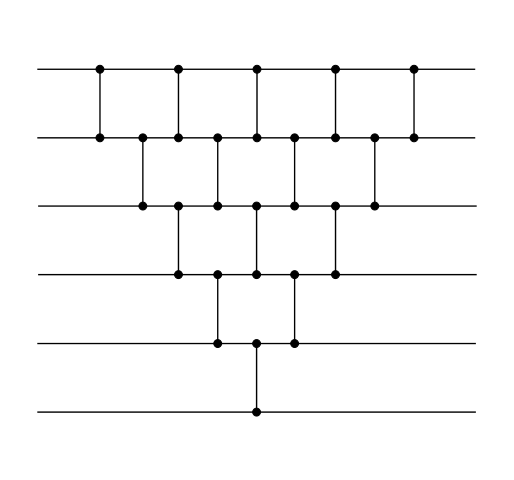
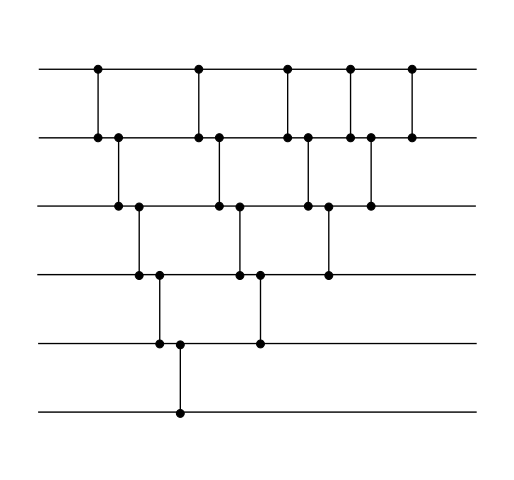
[[Файл:Parralelsort.png]] | [[Файл:Parralelsort.png]] | ||
| Строка 34: | Строка 45: | ||
=== Сортировка выбором === | === Сортировка выбором === | ||
| − | [[Файл: | + | Сеть для [[Сортировка выбором | сортировки выбором]] выглядит иначе. При переходе к сети с <tex> n + 1 </tex> входами, добавляется <tex> n </tex> компараторов: <tex> [0:1],[0:2]\dots[0:n] </tex>, . |
| + | |||
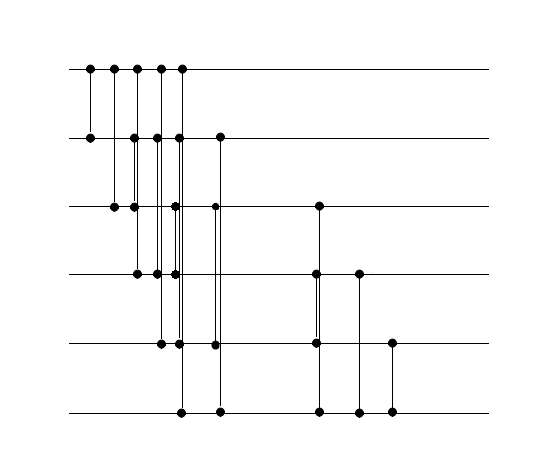
| + | [[Файл:Choosesortparralel2.png]] | ||
| + | |||
| + | {{ | ||
| + | Утверждение | ||
| + | |statement= | ||
| + | В результирующей сети будет <tex>2n - 3</tex> слоев, где <tex> n </tex> — количество входов. | ||
| + | |proof= | ||
| + | Определим операцию вложения компаратора <tex> [i:j] </tex> в компаратор <tex> [t:s] </tex> : разместим компаратор <tex> [i:j] </tex> и <tex> [t:s] </tex> на одном слое, так, что <tex> t < i < j < s </tex>. | ||
| + | |||
| + | Теперь воспользуемся принципом математической индукции. | ||
| + | |||
| + | '''База индукции''': | ||
| + | |||
| + | <tex> n = 2 </tex>. В сети всего два входа, на которых располагается один компаратор, тем самым наше предположение выполняется. | ||
| + | |||
| + | '''Шаг индукции''': | ||
| + | |||
| + | Пусть <tex> S(n) </tex> — количество слоев в сети сортировки с <tex> n </tex> входами. | ||
| + | |||
| + | При переходе от сортирующей сети с <tex>n</tex> входами к сети с <tex>n + 1</tex> входами, добавляем <tex> n </tex> компараторов <tex>\left( [0:1] \dots [0:n]\right) </tex>. Заметим, что в <tex> n - 2 </tex> добавленных компаратора можно вложить <tex> n - 2 </tex> компараторов из предыдущей сети, так, вкладывая один компаратор в другой, образуется новый слой, т.е. количество слоев не изменяется. Тогда останется два компаратора: <tex>[0:1], [0:2] </tex> в которые ничего нельзя вложить, т.е. количество слоев изменяется на <tex> 2 = S(n + 1) - S(n) </tex>. | ||
| + | |||
| + | Тогда наш переход выполняется и формула верна. Что и требовалось доказать. | ||
| + | |||
| + | }} | ||
| + | |||
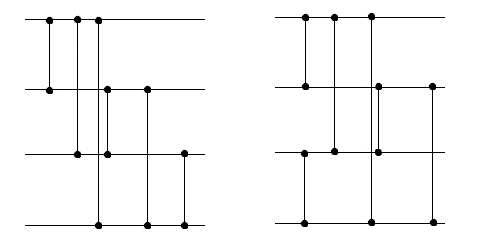
| + | Пример правильной и ошибочной сети для <tex> n = 4 </tex>. Если перенести свободные компараторы и слить их в один слой, то можно уменьшить количество слоев, но при этом сеть перестает быть сортирующей (при <tex> n = 4 </tex> ошибка будет возникать на последовательности <tex> [0,1,0,0] </tex>). | ||
| + | |||
| + | [[Файл:MyRis.jpg]] | ||
| + | |||
| + | ==См.также== | ||
| + | * [[Сортировочные сети с особыми свойствами]] | ||
| + | |||
| + | == Источники информации== | ||
| + | *Дональд Э. Кнут. Искусство программирования. Том 3. Сортировка и Поиск. стр. 238— ISBN 0-201-89685-0 | ||
| + | *Кормен, Томас Х.,Рональд Л., Штайн, Клифорд. Глава 27. Сортирующие сети // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-e издание. — М.: «Вильямс», 2005. — С. 799 - 822. — ISBN 5-8459-0857-4. | ||
| + | *[https://ru.wikipedia.org/wiki/%D0%A1%D0%B5%D1%82%D1%8C_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B8 Википедия — Сети сортировки] | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| − | + | [[Категория: Сортирующие сети]] | |
| − | |||
Текущая версия на 19:19, 4 сентября 2022
Рассмотрим модели сортирующих сетей для квадратичных сортировок.
Содержание
Сортирующие сети с последовательной сортировкой
На один слой будем устанавливать только один компаратор. Все последующие сети получаются простым моделированием соответствующих сортировок.
| Сортировка пузырьком | Сортировка вставками | Сортировка выбором |
 |
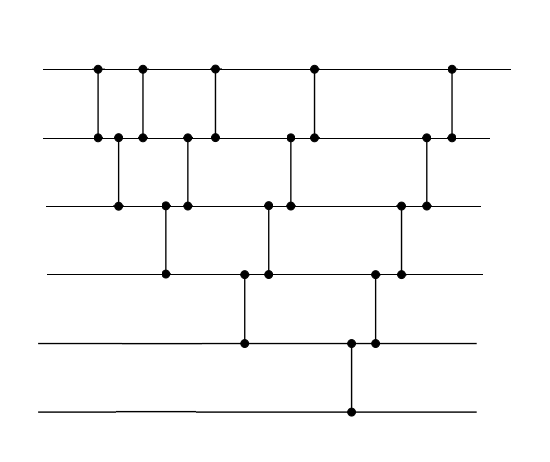 |
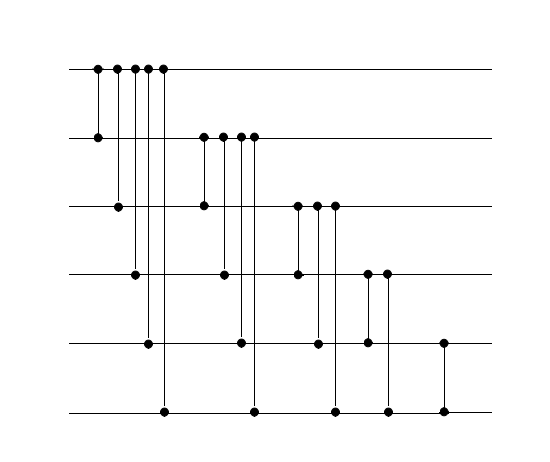
|
Сортирующие сети с параллельной сортировкой
На один слой устанавливается несколько компараторов.
Сортировка пузырьком и вставками
Заметим, что если сжать последовательные сортирующие сети пузырьком и вставками, то результат будет одним и тем же. Это видно из симметрии расположения компараторов на картинках выше.
| Утверждение: |
В результирующей сети будет слоев, где — количество входов. |
|
Докажем данное утверждение по принципу математической индукции. База индукции: При . В сети всего два входа, на которых располагается один компаратор, тем самым наше предположение выполняется. Шаг индукции: Пусть — количество слоев в сети сортировки. При переходе от сортирующей сети с входами к сети с входами, добавляем дополнительных компараторов ( или , т.к. возможны две стратегии добавления; отсюда, кстати, тоже видна эквивалентность схем для обоих сортировок). Будем также поддерживать сортирующую сеть в виде "треугольной" сети. Таким образом компараторы можно расположить в существующих слоях над самым верхним компаратором в соответствующем слое. То есть в сети с входами был слой с единственным компаратором , поэтому над ним можно разместить компаратор , на — . Затем на следующем слое будет уже два компаратора: над , поэтому сверху можно добавить . В общем виде, на слое с номером с конца (до середины треугольника), будет компараторов, последним из которых является , следовательно, на этот слой можно добавить компаратор . Значит, новые слои создадутся лишь благодаря компаратором и , поэтому число слоёв в новой сети составит , что удовлетворяет нашему соотношению. |
Сортирующая сеть для :
Сортировка выбором
Сеть для сортировки выбором выглядит иначе. При переходе к сети с входами, добавляется компараторов: , .
| Утверждение: |
В результирующей сети будет слоев, где — количество входов. |
|
Определим операцию вложения компаратора в компаратор : разместим компаратор и на одном слое, так, что . Теперь воспользуемся принципом математической индукции. База индукции: . В сети всего два входа, на которых располагается один компаратор, тем самым наше предположение выполняется. Шаг индукции: Пусть — количество слоев в сети сортировки с входами. При переходе от сортирующей сети с входами к сети с входами, добавляем компараторов . Заметим, что в добавленных компаратора можно вложить компараторов из предыдущей сети, так, вкладывая один компаратор в другой, образуется новый слой, т.е. количество слоев не изменяется. Тогда останется два компаратора: в которые ничего нельзя вложить, т.е. количество слоев изменяется на . Тогда наш переход выполняется и формула верна. Что и требовалось доказать. |
Пример правильной и ошибочной сети для . Если перенести свободные компараторы и слить их в один слой, то можно уменьшить количество слоев, но при этом сеть перестает быть сортирующей (при ошибка будет возникать на последовательности ).
См.также
Источники информации
- Дональд Э. Кнут. Искусство программирования. Том 3. Сортировка и Поиск. стр. 238— ISBN 0-201-89685-0
- Кормен, Томас Х.,Рональд Л., Штайн, Клифорд. Глава 27. Сортирующие сети // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-e издание. — М.: «Вильямс», 2005. — С. 799 - 822. — ISBN 5-8459-0857-4.
- Википедия — Сети сортировки