|
Приведем доказательство по индукции по числу вершин в цикле. Пусть [math] n [/math] - количество вершин в графе.
База индукции:
| Утверждение: |
Cильно связанный турнир [math] T [/math] из [math] n \geq 3 [/math] вершин содержит цикл длины [math] 3 [/math]. |
| [math]\triangleright[/math] | |
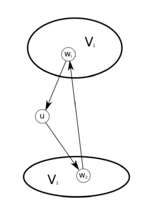
Пусть [math] u [/math] - произвольная вершина турнира [math] T [/math]. Множество вершин [math] VT - u [/math] распадается на [math] 2 [/math] непересекающихся множества:
- [math] V_1 = \{ v_1 \in VT | (v_1, u) \in ET \} [/math],
- [math] V_2 = \{ v_2 \in VT | (u, v_2) \in ET \} [/math].
[math] T [/math] сильно связен, следовательно:
- [math] V_1 \neq \emptyset [/math], (иначе [math] v [/math] - исток турнира)
- [math] V_2 \neq \emptyset [/math], (иначе [math] v [/math] - сток турнира)
- [math] \exists e = (w_2, w_1) \in ET [/math], (иначе нет пути из [math]V_2[/math] в [math]V_1[/math]):
- [math] w_1 \in V_1 [/math],
- [math] w_2 \in V_2 [/math].
Цикл [math] S_3: (u \rightarrow w_2 \rightarrow w_1 \rightarrow u) [/math] - искомый цикл длины [math] 3 [/math], q.e.d. | | [math]\triangleleft[/math] |
Индукционный переход:
| Утверждение: |
Если сильно связанный турнир [math] T [/math] из [math] n \geq 3 [/math] вершин содержит цикл [math] S_k [/math] длины [math] k [/math], то он содержит и цикл длины [math] k + 1 [/math]. |
| [math]\triangleright[/math] | |
Пусть [math] S_k = (v_1 \rightarrow v_2 \rightarrow \ldots \rightarrow v_k \rightarrow v_1) [/math].
Пусть [math] v_0 \notin S_k [/math] такая, что [math] \exists u, w \in S_k [/math]:
- [math] (v_0, u) \in ET [/math],
- [math] (w, v_0) \in ET [/math].
Рассмотрим два случая:
- существует такая вершина [math] v_0 [/math],
- не существует такой вершины [math] v_0 [/math].
Первый случай:
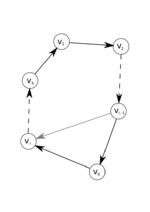 [math] S_{k + 1} в первом случае. [/math] - Пусть [math] v_1 [/math] - вершина из [math] S_k [/math] такая, что ребро [math] e = (v_1, v_0 ) \in ET [/math]. Пусть [math] v_i [/math] – первая вершина при обходе [math] S_k [/math] из [math] v_1 [/math], для которой ребро [math] f = (v_0, v_i ) \in ET [/math].
- Тогда ребро [math] g = (v_{i - 1}, v_0) \in ET [/math].
- Тогда [math] S_{k + 1} = (v_1 \rightarrow v_2 \rightarrow \ldots \rightarrow v_{i - 1} \rightarrow v_0 \rightarrow v_i \rightarrow \ldots \rightarrow v_k \rightarrow v_1) [/math] – искомый цикл длины [math] k + 1 [/math].
Второй случай:
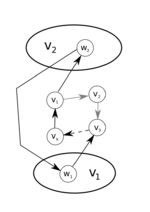 [math] S_{k + 1} во втором случае. [/math] - Пусть:
- [math] V_1 = \{ u \in VT | u \notin S_k, e = (u, v_i) \in ET, \forall i = \overline{1, n} \} [/math],
- [math] V_2 = \{ u \in VT | u \notin S_k, f = (v_i, u) \in ET, \forall i = \overline{1, n} \} [/math].
- Тогда [math] V_1 \cap V_2 = \emptyset [/math].
- Турнир сильно связен, следовательно:
- [math] V_1 \neq \emptyset [/math], (иначе [math] T [/math] не будет сильно связным, так как тогда нет простых путей с началом в [math] V_2 [/math] и концом в [math] {v_1, \ldots, v_k} [/math])
- [math] V_2 \neq \emptyset [/math], (иначе [math] T [/math] не будет сильно связным, так как тогда нет простых путей с началом в [math] {v_1, \ldots, v_k} [/math] и концом в [math] V_1 [/math])
- [math] \exists g = (w_2, w_1) \in ET [/math], (иначе [math]T[/math] не будет сильно связным, так как тогда нет простых путей с началом в [math]V_2[/math] и концом в [math]V_1[/math]):
- [math] w_1 \in V_1 [/math],
- [math] w_2 \in V_2 [/math].
- Тогда [math] S_{k + 1} = (v_1 \rightarrow w_2 \rightarrow w_1 \rightarrow v_3 \rightarrow \ldots \rightarrow v_k \rightarrow v_1) [/math] – искомый цикл длины [math] k + 1 [/math].
Цикл [math] S_{k + 1} [/math] - искомый цикл длины [math] k + 1 [/math], q.e.d. | | [math]\triangleleft[/math] |
Таким образом, в любой сильно связанный турнир [math] T [/math] из [math] n \geq 3 [/math] вершин содержит цикл длины [math] n [/math], то есть гамильтонов цикл, q.e.d.{ |