Метод Лупанова синтеза схем

Формулировка

Теорема:

Любая булева функция от [math]n[/math] аргументов [math]f(x_1, x_2, ..., x_n)[/math] при базисе [math]B = \{\neg, \lor, \land\}[/math] имеет схемную сложность [math]size_B (f) \lesssim \frac{2^n}{n}[/math].

Представление функции

Рис. 1. Описываемая таблица истинности, разделённая на полосы

Для начала поделим аргументы функции на два блока: первые [math]k[/math] и оставшиеся [math](n - k)[/math].

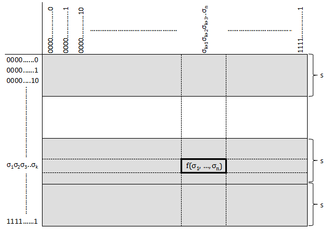
Для удобства дальнейших рассуждений представим булеву функцию в виде таблицы, изображённой на рис. 1.

• По горизонтали на ней представлены все значения [math]f(\sigma_1, \sigma_2, ..., \sigma_k, x_{k + 1}, x_{k + 2}, ..., x_n)[/math] (здесь и далее [math]\sigma[/math] - фиксированное значение, [math]x[/math] - переменное);
• По вертикали на ней представлены все значения [math]f(x_1, x_2, ..., x_k, \sigma_{k + 1}, \sigma_{k + 2}, ..., \sigma_n)[/math].

Таким образом, легко заметить, что значение [math]f(x_1, x_2, ..., x_n)[/math] находится на пересечении строки [math]x_1, x_2, ..., x_k[/math] и столбца [math]x_{k + 1}, x_{k + 2}, ..., x_n[/math].

Разделение на полосы

Разделим таблицу на горизонтальные полосы шириной [math]s[/math] (последняя полоса, возможно, будет короче остальных; её длину обозначим [math]s'[/math]). Пронумеруем полосы сверху вниз от 1 до [math]p=\lceil\frac{2^k}{s}\rceil[/math].

Рассмотрим независимо некоторую полосу. Среди её столбцов при небольшом [math]s[/math] будет много повторений, поэтому введём понятие сорта столбца.

Определение:

Сорт столбца полосы - класс эквивалентности, к которому столбец принадлежит (два столбца эквивалентны, если совпадают по значениям).

Число сортов столбцов [math]i[/math]-й полосы обозначим как [math]t(i)[/math]. Понятно, что для любой полосы [math]t(i) \leq 2^s[/math] (для последней [math]t(i) \leq 2^{s'}[/math]).

Функция для одной полосы

Рис. 2. Значения, возвращаемые функцией [math]g_{ij}[/math]

Пусть для некоторого [math]i[/math]

• [math]\beta_{j}[/math] - столбец [math]i[/math]-й полосы [math]j[/math]-го сорта;
• [math](\sigma_1^l, \sigma_2^l, ..., \sigma_k^l)[/math] - аргументы функции, соответствующие её значениям в [math]l[/math]-й строке [math]i[/math]-й полосы.

Тогда введём булеву функцию

[math]g_{ij}(x_1, x_2, ..., x_k) = \begin{cases} \beta_{jl}& , \mbox{if } \exists l \in [1; s]~(x_1, x_2, ..., x_k) = (\sigma_1^l, \sigma_2^l, ..., \sigma_k^l) \\ 0&, \mbox{else} \end{cases}[/math]

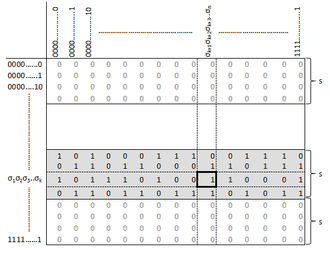
Другими словами, если строка, соответствующая аргументам функции [math]x_1, x_2, ..., x_k[/math], находится в [math]i[/math]-й полосе, то функция возвращает значение, записанное в столбце сорта [math]j[/math] для этой строки. Если же эта строка находится в другой полосе, то функция вернёт 0. Иллюстрация принципа работы функции [math]g_{ij}[/math] приведена на рис. 2.

Вывод исходной функции для фиксированной части параметров

Поскольку изначальный столбец [math](\sigma_{k + 1}, \sigma_{k + 2}, ..., \sigma_{n})[/math] складывается из столбцов соответствующих сортов в полосах, [math]f(x_1, x_2, ..., x_k, \sigma_{k + 1}, \sigma_{k + 2}, ..., \sigma_{n}) = \bigvee\limits_{i = 1}^p g_{ij_i}(x_1, x_2, ..., x_k)[/math], где [math]j_i[/math] - номер сорта столбца полосы [math]i[/math], являющегося соответствующей частью столбца [math](\sigma_{k + 1}, \sigma_{k + 2}, ..., \sigma_{n})[/math].

Мультиплексор и дешифратор

Для упрощения доказательства теоремы введём элементы мультиплексор и дешифратор.

Определение:

Мультиплексор - логический элемент, получающий на вход [math]2^n[/math] булевых значений; [math]n[/math]-значное число [math]x[/math] в двоичном представлении и возвращающий значение на [math]x[/math]-м входе.

Определение:

Дешифратор - логический элемент, получающий на вход булево значение [math]z[/math]; [math]n[/math]-значное число [math]x[/math] в двоичном представлении и выводящий [math]z[/math] на [math]x[/math]-й из своих [math]2^n[/math] выходов. На все остальные выходы элемент выдаёт 0.

Рис. 3. Мультиплексор слева, дешифратор справа

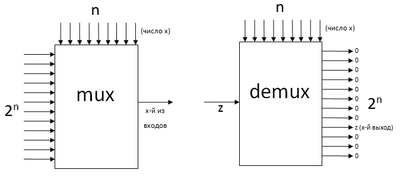
Иллюстрации элементов приведены на рис. 3.

Можно доказать, что оба элемента представимы схемами с числом элементов [math]\sim 2^n[/math] с помощью базиса [math]B[/math].

Доказательство

Иллюстрация частного случая представления Лупанова, описанного здесь

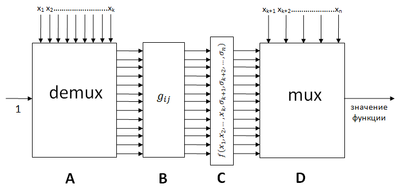
В качестве доказательства ниже будет предложен вариант такой схемы для произвольной функции [math]f(x_1, x_2, ..., x_n)[/math] (представление Лупанова). Для удобства поделим схему на блоки:

• Блок A - дешифратор, которому на вход подали 1 и [math](x_1, x_2, ..., x_k)[/math] в качестве двоичного представления числа.

Число элементов [math]L_A \sim 2^k[/math]

• Блок B - схемная реализация всех [math]g_{ij}[/math]. Функцию [math]g_{ij}[/math] можно реализовать как [math]\bigvee\limits_{\beta_l = 1} y_{il}[/math], где [math]y_{il}[/math] - выдал ли дешифратор "1" на [math]l[/math]-м выходе [math]i[/math]-й полосы.

Число элементов [math]L_B \leq (s - 1) \cdot (t(1) + t(2) + ... + t(p)) \lt sp \cdot 2^{s}[/math]

• Блок C - схемная реализация всех [math]f(x_1, x_2, ..., x_k, \sigma_{k + 1}, \sigma_{k + 2}, ..., \sigma_n)[/math].

Число элементов [math]L_C \sim p \cdot 2^{n - k} = \frac{2^n}{s}[/math]

• Блок D - мультиплексор, получающий на вход все [math]f(x_1, x_2, ..., x_k, \sigma_{k + 1}, \sigma_{k + 2}, ..., \sigma_n)[/math] и параметры функции [math]x_{k + 1}, x_{k + 2}, ..., x_n[/math] в качестве двоичного представления числа.

Число элементов [math]L_D \sim 2^{n - k}[/math]

Результат работы схемы - вывод мультиплексора.

Положим [math]s = [n - 2\log_2 n][/math]; [math]k = [\log_2 n][/math]. Тогда

• [math]L_A \sim 2^{\log_2 n} \lesssim \frac{2^n}{n}[/math]
• [math]L_B \lt sp \cdot 2^s = 2^{k + s} = \frac{2^n}{n}[/math]
• [math]L_C \sim \frac{2^n}{s} \sim \frac{2^n}{n}[/math]
• [math]L_D \sim 2^{n - k} = \frac{2^n}{n}[/math]

Итого, имеем схему с итоговым числом элементов [math]\sim \frac{2^n}{n}[/math], откуда следует, что [math]size_B (f) \lesssim \frac{2^n}{n}[/math], ч.т.д.

Ссылки

• Wikipedia - Multiplexer

Литература

• Яблонский С.В. Введение в дискретную математику, изд. Наука, 1986, стр. 361 - более обобщённое доказательство, частично взятое за основу.