Visibility graph и motion planning — различия между версиями
Igorjan94 (обсуждение | вклад) м (→Построение visibility графа) |
Igorjan94 (обсуждение | вклад) м |
||
| Строка 5: | Строка 5: | ||
== Visibility graph == | == Visibility graph == | ||
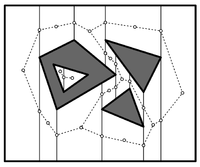
[[Файл:trap.png|200px|thumb|left|Путь с препятствиями через трапецоидную карту]] | [[Файл:trap.png|200px|thumb|left|Путь с препятствиями через трапецоидную карту]] | ||
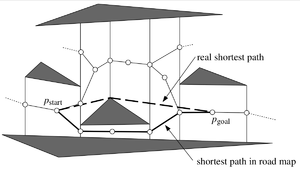
| − | [[Файл:notShort.png| | + | [[Файл:notShort.png|300px|thumb|right|Такой путь не самый короткий]] |
В общем, когда мы ищем путь от точки <tex> S </tex> до <tex> T </tex> с препятствиями (надо уточнить, что двигаем мы точку, а не какой-то полигон), можно построить [[Трапецоидная карта | трапецоидную карту]], соединить ребрами середины вертикальных сторон с центрами трапецоидов и в этом графе [[Алгоритм Дейкстры | Дейкстрой]] найти путь от <tex> S </tex> до <tex> T </tex>. Но этот путь не будет кратчайшим(кэп). | В общем, когда мы ищем путь от точки <tex> S </tex> до <tex> T </tex> с препятствиями (надо уточнить, что двигаем мы точку, а не какой-то полигон), можно построить [[Трапецоидная карта | трапецоидную карту]], соединить ребрами середины вертикальных сторон с центрами трапецоидов и в этом графе [[Алгоритм Дейкстры | Дейкстрой]] найти путь от <tex> S </tex> до <tex> T </tex>. Но этот путь не будет кратчайшим(кэп). | ||
| Строка 25: | Строка 25: | ||
==== <tex> O(n ^ 2 log n) </tex> ==== | ==== <tex> O(n ^ 2 log n) </tex> ==== | ||
Однако можно это сделать за <tex> O(n ^ 2 log n) </tex>. Пусть мы хотим из вершины <tex> v </tex> найти все видимые из нее вершины. Теперь мы будем перебирать ребра не в случайном порядке, а так чтобы можно было проверять за логарифм. | Однако можно это сделать за <tex> O(n ^ 2 log n) </tex>. Пусть мы хотим из вершины <tex> v </tex> найти все видимые из нее вершины. Теперь мы будем перебирать ребра не в случайном порядке, а так чтобы можно было проверять за логарифм. | ||
| − | + | ||
Для этого посортим все вершины по полярному углу (только те, которые справа нашей, ибо очевидно, что назад можно уже не смотреть) и запилим сбалансированное двоичное дерево поиска. | Для этого посортим все вершины по полярному углу (только те, которые справа нашей, ибо очевидно, что назад можно уже не смотреть) и запилим сбалансированное двоичное дерево поиска. | ||
Вершин у нас <tex> O(n) </tex>, сортим за <tex> O(n log n) </tex> плюс запросы в дереве за <tex> O(n) * O(log n) </tex>. Итого что хотели. | Вершин у нас <tex> O(n) </tex>, сортим за <tex> O(n log n) </tex> плюс запросы в дереве за <tex> O(n) * O(log n) </tex>. Итого что хотели. | ||
| + | ==== <tex> O(n ^ 2) </tex> ==== | ||
| + | Каким-то магическим образом, можно избавиться и от логарифма в асимптотике. Это делается с помощью [http://bit.ly/1eEqTzk rotation tree]. Про него рассказывал Антон Ков., но как-то мутно и не очень понятно. Суть такова, что мы обходим вершины в таком хитром порядке, что почти не просматриваем лишнее и получаем асимптотику {{---}} квадрат. | ||
| + | |||
== Motion planning == | == Motion planning == | ||
В общем тут все очевидно. Тут мы просто двигаем не точку, а произвольный выпуклый полигон. Если мы его не можем вращать, просто "обводим" препятствия нашим полигоном (запиливаем [[Сумма Минковского (определение, вычисление)|сумму Минковского]] препятствий и полигона) и получаем другие препятствия, но зато теперь мы двигаем точку. А это мы уже научились делать выше. | В общем тут все очевидно. Тут мы просто двигаем не точку, а произвольный выпуклый полигон. Если мы его не можем вращать, просто "обводим" препятствия нашим полигоном (запиливаем [[Сумма Минковского (определение, вычисление)|сумму Минковского]] препятствий и полигона) и получаем другие препятствия, но зато теперь мы двигаем точку. А это мы уже научились делать выше. | ||
Версия 17:18, 7 января 2014
| Конспект написан не до конца, но основные вещи уже есть. |
Содержание
Visibility graph
В общем, когда мы ищем путь от точки до с препятствиями (надо уточнить, что двигаем мы точку, а не какой-то полигон), можно построить трапецоидную карту, соединить ребрами середины вертикальных сторон с центрами трапецоидов и в этом графе Дейкстрой найти путь от до . Но этот путь не будет кратчайшим(кэп).
| Лемма: |
Любой кратчайший путь от до с полигональными препятствиями представляет собой ломаную, вершины которой — вершины полигонов. |
| Доказательство: |
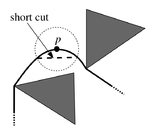
| Пусть путь проходит(в смысле вершины) через какую-то другую точку. Рассмотрим окрестность этой точки. По неравенству треугольника мы сможем немножко, да срезать. Значит этот путь не кратчайший. Противоречие, значит лемма доказана и все офигенно. |
По этой лемме запилим visibility graph. Его вершины — вершины полигонов. Между вершинами и существует ребро, если из видна (mutually visible) (ребра полигонов тоже входят в этот граф). Теперь, если мы добавим к множеству вершин и (и ребра в видимые вершины), у нас получится граф, в котором опять же Дейкстрой находим кратчайший путь. По лемме любое ребро кратчайшего пути — ребро visibility графа, так что мы нашли то, что нужно.
Построение visibility графа
Если делать в тупую наивно, т. е. для каждой пары вершин проверять можно ли добавить ли такое ребро(нет ли пересечений с полигонами), будет (зато просто пилится).
Однако можно это сделать за . Пусть мы хотим из вершины найти все видимые из нее вершины. Теперь мы будем перебирать ребра не в случайном порядке, а так чтобы можно было проверять за логарифм.
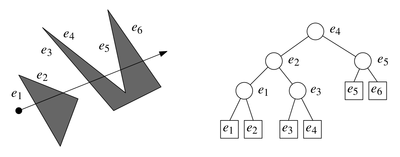
Для этого посортим все вершины по полярному углу (только те, которые справа нашей, ибо очевидно, что назад можно уже не смотреть) и запилим сбалансированное двоичное дерево поиска.
Вершин у нас , сортим за плюс запросы в дереве за . Итого что хотели.
Каким-то магическим образом, можно избавиться и от логарифма в асимптотике. Это делается с помощью rotation tree. Про него рассказывал Антон Ков., но как-то мутно и не очень понятно. Суть такова, что мы обходим вершины в таком хитром порядке, что почти не просматриваем лишнее и получаем асимптотику — квадрат.
Motion planning
В общем тут все очевидно. Тут мы просто двигаем не точку, а произвольный выпуклый полигон. Если мы его не можем вращать, просто "обводим" препятствия нашим полигоном (запиливаем сумму Минковского препятствий и полигона) и получаем другие препятствия, но зато теперь мы двигаем точку. А это мы уже научились делать выше.
Если же этот полигон можно вращать, то делаем примерно то же самое, только как-то по-хитрому. Нам про это, кажется, не рассказывали(или рассказывали так же:))
Источники
- Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 15 page 324-331