Visibility graph и motion planning
Содержание
Нахождение любого пути между точками с препятствиями
Для начала рассмотрим движение материальной точки. Случай, когда размером и формой движимого объекта пренебречь нельзя, будет рассмотрен позднее.
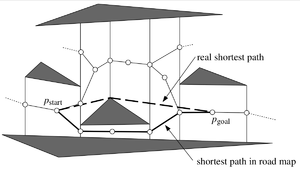
Эту задачу можно решить с помощью трапецоидной карты. По ней строится граф, ребра которого соединяют центры трапедоидов, а также начальную и конечную вершины с серединами вертикальных сторон трапецоидов. В таком графе ищется путь между начальной и конечной вершинами.
Если точки лежат внутри одного трапецоида — ответ найден. Иначе идём из стартовой точки в центр её трапецоида, далее по построенным рёбрам ищем трапецоид содержащий финальную точку. Для этого можно использовать поиск в ширину или другой алгоритм нахождения кратчайшего пути в графе. В конечном итоге, соединяем середину последнего трапецоида с конечной вершиной.
Данный алгоритм работает за и за линейное количество памяти и хорошо подходит для нахождения какого-нибудь пути между парой данных вершин. Но если нужно найти кратчайший путь, этот алгоритм не подходит, хоть и работает быстро. Однако, решения нахождения кратчайшего пути в лучшем случае работают за времени и памяти (здесь и далее — количество всех вершин).
Нахождение кратчайшего пути между точками с препятствиями
Visibility graph
Рассмотрим точное решение нахождения кратчайшего пути на плоскости между двумя точками с полигональными препятствиями с помощью построения графа видимости. После его построения, как и в случае с трапецоидной картой, кратчайший путь ищется любым стандартным алгоритмом поиска (например, алгоритмом Дейкстры или A*).
Для простоты рассуждений начальную и конечную вершины будем считать вершинами полигонов.
| Лемма (О кратчайшем пути): |
Любой кратчайший путь между двумя вершинами с полигональными препятствиями представляет собой ломаную, вершины которой — вершины полигонов. |
| Доказательство: |
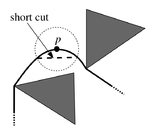
| Пусть кратчайший путь — не ломаная. В таком случае, на пути существует такая точка , которая не принадлежит ни одному прямому отрезку. Это означает, что существует -окрестность точки , в которую не попадает ни одно препятствие (случай, когда точка попала на ребро рассматривается аналогично). В таком случае, подпуть, который находится внутри -окрестности, по неравенству треугольника может быть сокращён по хорде, соединяющий точки пересечения границы -окрестности с путем. Раз часть пути может быть уменьшена, значит и весь путь может быть уменьшен, а значит исходное предположение некорректно. |
| Определение: |
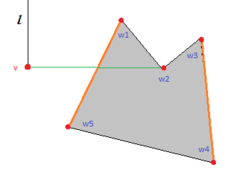
| Говорят, что вершина видна (англ. mutually visible) из , если отрезок не пересекает ни одного препятствия. |
| Определение: |
| Граф видимости (англ. visibility graph) — граф, вершины которого — вершины полигонов. Между вершинами и существует ребро, если из видна . |
В худшем случае в таком графе может быть ребер. Однако по некоторым ребрам кратчайший путь точно не пройдет, и такие ребра из графа можно удалить.
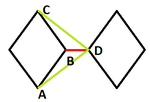
| Лемма (О неиспользуемых вершинах): |
|
| Доказательство: |
|
По доказанным леммам любое ребро кратчайшего пути содержится в графе. Таким образом, для нахождения кратчайшего пути осталось найти кратчайший путь в этом графе от начальной до конечной вершины.
Построение visibility графа
Наивный алгоритм.
Для каждой пары вершин проверяем, можно ли добавить ребро между ними, то есть нет ли пересечений с полигонами. пар вершин и ребер, то есть .
Lee’s Algorithm.
|
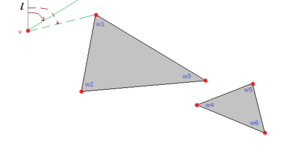
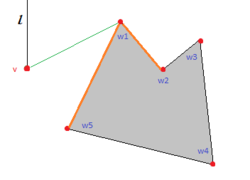
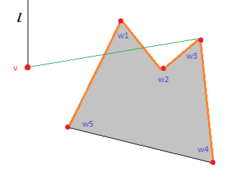
Однако можно это сделать за . Идея алгоритма проста: для каждой вершины найдем видимые из нее вершины. Если научиться делать это за , задача решена, так как всего точек . Для каждой вершины будем рассматривать только правую половину плоскости, так как ребра, которые должны идти в левую половину, будут исходить из вершин, для которых текущая вершина будет справа. Переформулируем задачу. Дано: точка и множество отрезков — ребер препятствий. Найти: множество концов отрезков, видимых из . Для решения этой задачи будем использовать заметающий луч с началом в точке . Его статусом будут отрезки, которые его пересекают, упорядоченные по возрастанию расстояния от точки до точки пересечения. Точками событий будут концы отрезков. Пустим луч из рассматриваемой вершины вертикально вверх и добавим в статус все отрезки, которые он пересекает, по увеличению расстояния до них. Теперь будем рассматривать точки в порядке сортировки по углу между и вертикальной полуосью . При таком обходе для проверки видимости вершины достаточно проверить пересечение с ближайшим к отрезком, то есть первым в статусе(так как отрезки отсортированы по расстоянию до них). Действительно, если вершина не видна, то отрезок пересекает несколько отрезков, лежащих перед , а значит и ближайший. В противном случае все пересекаемые лучом отрезки лежат за вершиной и пересечения отрезка с ближайшим отрезком не будет. Вне зависимости от видимости вершины, необходимо изменить статус заметающего луча. Для этого необходимо удалить из статуса все отрезки, которые заканчиваются вершине (лежат слева от прямой ) и добавить все отрезки, которые в ней начинаются (лежат справа от прямой ). Псевдокодgraph buildVisibilityGraph(Set<Segment> segments) vertices = getVertices(segments) graph = visibilityGraph(vertices) for Vertex in vertices for Vertex in getVisibleVertices(, segments) visibilityGraph.addEdge(, ) return visibilityGraph Здесь функция getVisibleVertices() возвращает все видимые из вершины и выглядит так: Set<Vertex> getVisibleVertices(Vertex , Set<Segment> segments) Set<Vertex> answer for Segment in segments if intersect(, ) status.add() for Point in segments if currentVertices.add() sort(currentVertices) by angle for Point in currentVertices if not intersect(, status.closest) answer.add() for Segment ending in status.delete() for Segment beginning in status.add() return answer В качестве статуса нужно использовать структуру данных, позволяющую добавлять и удалять из нее отрезки за и извлекать минимум за или . В этом случае достигается асимптотика , так как для каждой из точек выполняется сортировка за , обновление статуса (суммарно , так как каждый отрезок добавляется и удаляется из статуса не более одного раза) и запросы ближайшего отрезка ( или на точку, то есть или ). |
Motion planning
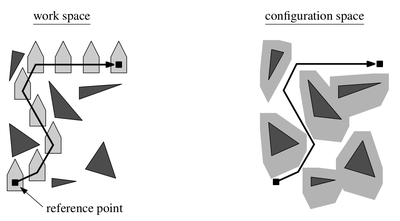
Рассмотрим задачу нахождения кратчайшего пути, когда движимый объект — это выпуклый полигон. Например, робот, которого надо доставить из начальной в конечную точку.
Если полигон вращать нельзя, задачу сводится к движению точки так: выбирается точка на полигоне, которая принимается за начало координат. В такой системе координат для каждого препятствия считается сумма Минковского с полигоном. Получаются бОльшие препятствия, но теперь достаточно двигать выбранную точку, что было описано выше.
Если полигон можно вращать, задача нахождения кратчайшего пути становится достаточно ресурсоёмка, поэтому обычно рассматривают задачу нахождения какого-нибудь пути между конечными точками.
Первый шаг решения этой задачи совпадает с предыдущим случаем: выберем точку и построим сумму Минковского препятствий с полигоном. Рассмотрим малый угол . Представим, что поворот полигона на этот угол — это движение вверх-вниз между слоями, на каждом из которых посчитана сумма Минковского с полигоном, повернутым на этот угол.
На каждом слое построим трапецоидную карту и граф, как описано в начале. Если пересечь соседние слои и добавить между их графами ребра, получится один большой граф, в котором ищется кратчайший путь.
При таком подходе может возникнуть ошибка при пересечении слоев: на каждом слое состояния будут допустимые, а осуществить поворот физически будет невозможно. Обычно, эту проблему решают двумя способами: измельчением угла поворота и изначальным сглаживанием углов полигона. Первый способ повышает не только точность решения, но и вычислительную сложность задачи. Второй подход практически исключает возможность нахождения пути, когда его нет, но повышает вероятность "ненахождения" пути, когда он есть.
Источники информации
- Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars, Computational Geometry: Algorithms and Applications — Third edition — Springer, 2008. — Chapter 15. — ISBN 978-3-540-77973-5
- Academia.edu — 3D Visibility Graph
- Хабрахабр — Motion planning: граф видимости, дорожные карты
- igitur-archive.library.uu.nl — Visibility graph при помощи rotation tree за .
Ссылки
- Github — Реализация алгоритма за