Visibility graph и motion planning

ВНИМАНИЕ!!! Данная статья написана исключительно по-пацански и обладает повышенной чёткостью.

Visibility graph

Путь с препятствиями через трапецоидную карту

Такой путь не самый короткий

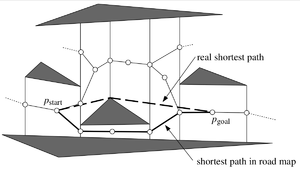
В общем, когда мы ищем путь от точки [math] S [/math] до [math] T [/math] с препятствиями (надо уточнить, что двигаем мы точку, а не какой-то полигон), можно построить трапецоидную карту, соединить ребрами середины вертикальных сторон с центрами трапецоидов и в этом графе Дейкстрой найти путь от [math] S [/math] до [math] T [/math]. Но этот путь не будет кратчайшим(кэп).

Лемма:

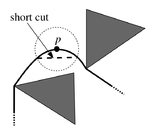
Любой кратчайший путь от [math] S [/math] до [math] T [/math] с полигональными препятствиями представляет собой ломаную, вершины которой — вершины полигонов.

Доказательство:

[math]\triangleright[/math]

Ну в общем тут все очевидно Пусть путь проходит(в смысле вершины) через какую-то другую точку. Рассмотрим окрестность этой точки. По неравенству треугольника мы сможем немножко, да срезать. Значит этот путь не кратчайший. Противоречие, значит лемма доказана и все офигенно.

[math]\triangleleft[/math]

По этой лемме запилим visibility graph. Его вершины — вершины полигонов. Между вершинами [math] u [/math] и [math] v [/math] существует ребро, если из [math] u [/math] видна (mutually visible) [math] v [/math] (ребра полигонов тоже входят в этот граф). Теперь, если мы добавим к множеству вершин [math] S [/math] и [math] T [/math] (и ребра в видимые вершины), у нас получится граф, в котором опять же Дейкстрой находим кратчайший путь. По лемме любое ребро кратчайшего пути — ребро visibility графа, так что мы нашли то, что нужно.

Построение visibility графа

Наивный алгоритм. [math] O(n ^ 3) [/math]

Если делать в тупую наивно, т. е. для каждой пары вершин проверять можно ли добавить ли такое ребро(нет ли пересечений с полигонами), будет [math] O(n^3) [/math] (зато просто пилится, даже не надо объяснять как).

Дерево поиска пересекаемых ребер

Lee’s Algorithm. [math] O(n ^ 2 \log n) [/math]

Однако можно это сделать за [math] O(n ^ 2 \log n) [/math]. Пусть мы хотим из вершины [math] v [/math] найти все видимые из нее вершины. Теперь мы будем перебирать ребра не в случайном порядке, а так чтобы можно было проверять за логарифм.

Для этого посортим все вершины по полярному углу (только те, которые справа нашей, ибо очевидно, что назад можно уже не смотреть) и запилим сбалансированное двоичное дерево поиска.

Вершин у нас [math] O(n) [/math], сортим за [math] O(n \log n) [/math] плюс запросы в дереве за [math] O(n) * O(\log n) [/math]. Итого что хотели.

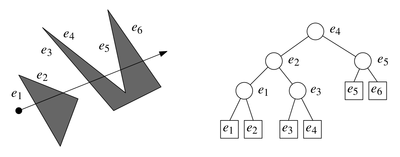
Overmars and Welzl’s Algorithm [math] O(n ^ 2) [/math]

Каким-то магическим образом, можно избавиться и от логарифма в асимптотике. Это делается с помощью rotation tree. Про него рассказывал Антон Ков., но как-то мутно и не очень понятно. Суть такова, что мы обходим вершины в таком хитром порядке, что почти не просматриваем лишнее и получаем асимптотику — квадрат.

Короче тут мы делаем то же самое, что и н2логн, только сортим не для каждой вершины отдельно, а рассматриваем все одновременно.

"The idea is simple: for each vertex, a scanline is kept which runs from [math] -\pi / 2 [/math] to [math] \pi / 2 [/math] hopping from vertex to vertex in its path. During the main loop, it appears that all of the scanlines are proceeding simultaneously. In fact, there are exact rules about determining the next vertex to process, and some vertices may finish their scan before others. To understand the rules about finding the next vertex, the rotation tree must be understood. A rotation tree is a rooted planar tree where each vertex is a node and points to its parent. There are two special nodes: [math] +\infty [/math] and [math] -\infty [/math]. Initially, all vertices point to [math] -\infty [/math] as their parent and [math] -\infty [/math] points to [math] +\infty [/math]. Also stored is the rightmost child (if a node is a parent), and its right and left siblings (if they exist). The ordering of children is by slope: the one with the smallest slope is the leftmost. The loop that examines all pairs simply takes the rightmost leftmost leaf as the next segment to process and then reattaches it to the tree (while maintaining the property of being a rotation tree). It can reattach to the left of its parent or to the tangent of the chain above it. When a vertex attaches to [math] +\infty [/math], it is finished. The loop continues when all points have attached to [math] +\infty [/math]".

/*мне лень это переводить, и так понятно/непонятно*/

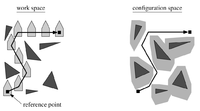
Motion planning

Раздуваем препятствия

Логично же

В общем тут все очевидно. Тут мы просто двигаем не точку, а произвольный выпуклый полигон. Если мы его не можем вращать, просто "обводим" препятствия нашим полигоном (запиливаем сумму Минковского препятствий и полигона, сдвинутого в начало координат какой-нибудь точкой) и получаем другие препятствия, но зато теперь мы двигаем точку. А это мы уже научились делать выше.

Если же этот полигон можно вращать, то делаем примерно то же самое, только как-то по-хитрому. Нам про это, кажется, не рассказывали(или рассказывали так же:))

Источники

• Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 15 page 324-331
• not_bad.jpg статья про visibility graphs