Цифровая сортировка — различия между версиями
Smnikita (обсуждение | вклад) |
Smnikita (обсуждение | вклад) |
||
| Строка 17: | Строка 17: | ||
Такой подход к алгоритму называют '''LSD-сортировкой''' (Least Significant Digit radix sort). Существует модификация алгоритма цифровой сортировки, анализирующая значения разрядов, начиная слева, с наиболее значащих разрядов. Данный алгоритм известен, как '''MSD-сортировка''' (Most Significant Digit radix sort). | Такой подход к алгоритму называют '''LSD-сортировкой''' (Least Significant Digit radix sort). Существует модификация алгоритма цифровой сортировки, анализирующая значения разрядов, начиная слева, с наиболее значащих разрядов. Данный алгоритм известен, как '''MSD-сортировка''' (Most Significant Digit radix sort). | ||
| − | === Корректность алгоритма === | + | === Корректность алгоритма LSD-сортировки === |
Докажем, что данный алгоритм работает верно, используя метод математической индукции по номеру разряда. Пусть <tex> n </tex> {{---}} количество разрядов в сортируемых объектах. | Докажем, что данный алгоритм работает верно, используя метод математической индукции по номеру разряда. Пусть <tex> n </tex> {{---}} количество разрядов в сортируемых объектах. | ||
| Строка 29: | Строка 29: | ||
=== LSD-сортировка === | === LSD-сортировка === | ||
В качестве примера рассмотрим сортировку чисел. Как говорилось выше, в такой ситуации в качестве устойчивой сортировки применяют сортировку подсчетом, так как обычно количество различных значений разрядов не превосходит количества сортируемых элементов. Ниже приведен псевдокод цифровой сортировки, которой подается массив <tex> A </tex> <tex> m </tex>-разрядных чисел размера <tex> n </tex>. Сам по себе алгоритм представляет собой цикл по номеру разряда, на каждой итерации которого элементы массива <tex> A </tex> размещаются в нужном порядке во вспомогательном массиве <tex> B </tex>. Для подсчета количества объектов, <tex> i </tex>-й разряд которых одинаковый, а затем и для определения положения объектов в массиве <tex> B </tex> используется вспомогательный массив <tex> C </tex>. Функция <tex> digit(x, i) </tex> возвращает <tex> i </tex>-й разряд числа <tex> x </tex>. Также считаем, что значения разрядов меньше <tex> k </tex>. | В качестве примера рассмотрим сортировку чисел. Как говорилось выше, в такой ситуации в качестве устойчивой сортировки применяют сортировку подсчетом, так как обычно количество различных значений разрядов не превосходит количества сортируемых элементов. Ниже приведен псевдокод цифровой сортировки, которой подается массив <tex> A </tex> <tex> m </tex>-разрядных чисел размера <tex> n </tex>. Сам по себе алгоритм представляет собой цикл по номеру разряда, на каждой итерации которого элементы массива <tex> A </tex> размещаются в нужном порядке во вспомогательном массиве <tex> B </tex>. Для подсчета количества объектов, <tex> i </tex>-й разряд которых одинаковый, а затем и для определения положения объектов в массиве <tex> B </tex> используется вспомогательный массив <tex> C </tex>. Функция <tex> digit(x, i) </tex> возвращает <tex> i </tex>-й разряд числа <tex> x </tex>. Также считаем, что значения разрядов меньше <tex> k </tex>. | ||
| − | radixSort(A) | + | '''function''' radixSort(int[] A) |
'''for''' i = 1 '''to''' m | '''for''' i = 1 '''to''' m | ||
'''for''' j = 0 '''to''' k - 1 | '''for''' j = 0 '''to''' k - 1 | ||
| Строка 35: | Строка 35: | ||
'''for''' j = 0 '''to''' n - 1 | '''for''' j = 0 '''to''' n - 1 | ||
d = digit(A[j], i) | d = digit(A[j], i) | ||
| − | C[d] + | + | C[d]++ |
count = 0 | count = 0 | ||
'''for''' j = 0 '''to''' k - 1 | '''for''' j = 0 '''to''' k - 1 | ||
tmp = C[j] | tmp = C[j] | ||
C[j] = count | C[j] = count | ||
| − | count = | + | count += tmp |
'''for''' j = 0 '''to''' n - 1 | '''for''' j = 0 '''to''' n - 1 | ||
d = digit(A[j], i) | d = digit(A[j], i) | ||
B[C[d]] = A[j] | B[C[d]] = A[j] | ||
| − | C[d] + | + | C[d]++ |
A = B | A = B | ||
=== MSD-сортировка === | === MSD-сортировка === | ||
| − | Сначала исходный массив делится на <tex>k</tex> частей, где <tex>k</tex> — основание, выбранное для представления сортируемых объектов. Эти части принято называть "корзинами" или "карманами". В первую корзину попадают элементы, у которых старший разряд с номером <tex>d = 0</tex> имеет значение <tex>0</tex>. Во вторую корзину попадают элементы, у которых старший разряд с номером <tex>d = 0</tex> имеет значение <tex>1</tex> и так далее. Затем элементы, попавшие в разные корзины, подвергаются рекурсивному разделению по следующему разряду с номером <tex>d = 1</tex>. Рекурсивный процесс разделения продолжается, пока не будут перебраны все разряды сортируемых объектов. | + | Будем считать, что у всех элементов одинаковое число разрядов. Если это не так, то положим на более старших разрядах элементы с самым маленьким значением — для чисел это 0. Сначала исходный массив делится на <tex>k</tex> частей, где <tex>k</tex> — основание, выбранное для представления сортируемых объектов. Эти части принято называть "корзинами" или "карманами". В первую корзину попадают элементы, у которых старший разряд с номером <tex>d = 0</tex> имеет значение <tex>0</tex>. Во вторую корзину попадают элементы, у которых старший разряд с номером <tex>d = 0</tex> имеет значение <tex>1</tex> и так далее. Затем элементы, попавшие в разные корзины, подвергаются рекурсивному разделению по следующему разряду с номером <tex>d = 1</tex>. Рекурсивный процесс разделения продолжается, пока не будут перебраны все разряды сортируемых объектов и пока размер корзины больше единицы. (то есть останавливаемся когда <tex>d > m</tex> или <tex>l \geq r</tex>, где m — максимальное число разрядов в сортируемых объектах, <tex>l</tex>, <tex>r</tex> — левая и правая границы отрезка массива <tex>A</tex>). |
| + | |||
В основу распределения элементов по корзинам положен метод распределяющего подсчета элементов с одинаковыми значениями в сортируемом разряде. Для этого выполняется просмотр массива и подсчет количества элементов с различными значениями в сортируемом разряде. Эти счетчики фиксируются во вспомогательном массиве счетчиков <tex>cnt</tex>. Затем счетчики используются для вычисления размеров корзин и определения границ разделения массива. В соответствии с этими границами сортируемые объекты переносятся во вспомогательный массив <tex>c</tex>, в котором размещены корзины. | В основу распределения элементов по корзинам положен метод распределяющего подсчета элементов с одинаковыми значениями в сортируемом разряде. Для этого выполняется просмотр массива и подсчет количества элементов с различными значениями в сортируемом разряде. Эти счетчики фиксируются во вспомогательном массиве счетчиков <tex>cnt</tex>. Затем счетчики используются для вычисления размеров корзин и определения границ разделения массива. В соответствии с этими границами сортируемые объекты переносятся во вспомогательный массив <tex>c</tex>, в котором размещены корзины. | ||
После того как корзины сформированы, содержимое вспомогательного массива <tex>c</tex> переносится обратно в исходный массив <tex>A</tex> и выполняется рекурсивное разделение новых частей по следующему разряду в пределах границ корзин, полученных на предыдущем шаге. | После того как корзины сформированы, содержимое вспомогательного массива <tex>c</tex> переносится обратно в исходный массив <tex>A</tex> и выполняется рекурсивное разделение новых частей по следующему разряду в пределах границ корзин, полученных на предыдущем шаге. | ||
| − | <tex> | + | Изначально запускаем функцию так <tex>radixSort(A, 1, A.length, 1)</tex> |
| − | + | '''function''' radixSort(int[] A, int l, int r, int d) | |
| − | radixSort(A, l, r, d) | + | '''if''' d > m '''or''' l >= r |
| − | '''if''' d > m '''or''' l >= r '''return''' | + | '''return''' |
'''for''' j = 0 '''to''' k + 1 | '''for''' j = 0 '''to''' k + 1 | ||
cnt[j] = 0 | cnt[j] = 0 | ||
'''for''' i = l '''to''' r | '''for''' i = l '''to''' r | ||
j = digit(A[i], d) | j = digit(A[i], d) | ||
| − | cnt[j + 1] | + | cnt[j + 1]++ |
'''for''' j = 2 '''to''' k | '''for''' j = 2 '''to''' k | ||
| − | cnt[j] = | + | cnt[j] += cnt[j - 1] |
'''for''' i = l '''to''' r | '''for''' i = l '''to''' r | ||
j = digit(A[i], d) | j = digit(A[i], d) | ||
c[l + cnt[j]] = A[i] | c[l + cnt[j]] = A[i] | ||
| − | + | cnt[j]++ | |
'''for''' i = l '''to''' r | '''for''' i = l '''to''' r | ||
A[i] = c[i] | A[i] = c[i] | ||
| Строка 81: | Строка 82: | ||
Если количество разрядов {{---}} константа, а <tex> k = O(n) </tex>, то сложность цифровой сортировки составляет <tex> O(n) </tex>, то есть она линейно зависит от количества сортируемых чисел. | Если количество разрядов {{---}} константа, а <tex> k = O(n) </tex>, то сложность цифровой сортировки составляет <tex> O(n) </tex>, то есть она линейно зависит от количества сортируемых чисел. | ||
| − | == | + | Сложность MSD-сортировки оценивается величиной <tex>O(n \log_k n)</tex>. При больших k величина <tex>\log_k n</tex> становится малой и сложность становится линейной функцией <tex>O(n)</tex> |
| + | |||
| + | Существует так же модификация MSD-сортировки, при которой рекурсивный процесс останавливается при небольших размерах текущего кармана и вызывается более быстрая сортировка основанная на сравнениях (например, сортировка вставками). | ||
| + | |||
| + | Таким образом, если k небольшое, то лучше использовать LSD-сортировку, при больших k {{---}} MSD-сортировку. | ||
| + | == Источники информации == | ||
* Дональд Кнут Искусство программирования, том 3. Сортировка и поиск | * Дональд Кнут Искусство программирования, том 3. Сортировка и поиск | ||
* Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ | * Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ | ||
| − | |||
| − | |||
* [http://rain.ifmo.ru/cat/view.php/vis/sorts/linear-2005 Визуализатор 1] — Java-аплет. | * [http://rain.ifmo.ru/cat/view.php/vis/sorts/linear-2005 Визуализатор 1] — Java-аплет. | ||
* [http://rain.ifmo.ru/cat/view.php/vis/sorts/linear-2001 Визуализатор 2] — Java-аплет. | * [http://rain.ifmo.ru/cat/view.php/vis/sorts/linear-2001 Визуализатор 2] — Java-аплет. | ||
| + | == Смотри также == | ||
| + | * [[Сортировка подсчетом]] | ||
| + | * [[Сортировка вставками]] | ||
| + | * [[wikipedia:ru:Поразрядная сортировка|Википедия {{---}} Цифровая сортировка]] | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Сортировки]] | [[Категория: Сортировки]] | ||
Версия 18:39, 20 мая 2014
Цифровая сортировка — один из алгоритмов сортировки, использующих внутреннюю структуру сортируемых объектов.
Содержание
Алгоритм
Имеем множество последовательностей одинаковой длины, состоящих из элементов, на которых задано отношение линейного порядка. Требуется отсортировать эти последовательности в лексикографическом порядке.
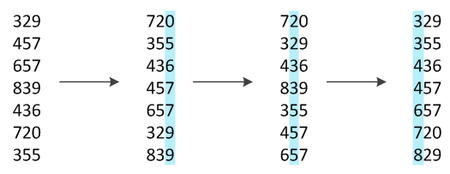
По аналогии с разрядами чисел будем называть элементы, из которых состоят сортируемые объекты, разрядами. Сам алгоритм состоит в последовательной сортировке объектов какой-либо устойчивой сортировкой по каждому разряду, в порядке от младшего разряда к старшему, после чего последовательности будут расположены в требуемом порядке.
Примерами объектов, которые удобно разбивать на разряды и сортировать по ним, являются числа и строки.
- Для чисел уже существует понятие разряда, поэтому будем представлять числа как последовательности разрядов. Конечно, в разных системах счисления разряды одного и того же числа отличаются, поэтому перед сортировкой представим числа в удобной для нас системе счисления.
- Строки представляют из себя последовательности символов, поэтому в качестве разрядов в данном случае выступают отдельные символы, сравнение которых обычно происходит по соответствующим им кодам из таблицы кодировок. Для такого разбиения самый младший разряд — последний символ строки.
Для вышеперечисленных объектов наиболее часто в качестве устойчивой сортировки применяют сортировку подсчетом.
Такой подход к алгоритму называют LSD-сортировкой (Least Significant Digit radix sort). Существует модификация алгоритма цифровой сортировки, анализирующая значения разрядов, начиная слева, с наиболее значащих разрядов. Данный алгоритм известен, как MSD-сортировка (Most Significant Digit radix sort).
Корректность алгоритма LSD-сортировки
Докажем, что данный алгоритм работает верно, используя метод математической индукции по номеру разряда. Пусть — количество разрядов в сортируемых объектах.
База: . Очевидно, что алгоритм работает верно, потому что в таком случае мы просто сортируем младшие разряды какой-то заранее выбранной устойчивой сортировкой.
Переход: Пусть для алгоритм правильно отсортировал последовательности по младшим разрядам. Покажем, что в таком случае, при сортировке по -му разряду, последовательности также будут отсортированы в правильном порядке.
Вспомогательная сортировка разобьет все объекты на группы, в которых -й разряд объектов одинаковый. Рассмотрим такие группы. Для сортировки по отдельным разрядам мы используем устойчивую сортировку, следовательно порядок объектов с одинаковым -м разрядом не изменился. Но по предположению индукции по предыдущим разрядам последовательности были отсортированы правильно, и поэтому в каждой такой группе они будут отсортированы верно. Также верно, что сами группы находятся в правильном относительно друг друга порядке, а, следовательно, и все объекты отсортированы правильно по -м младшим разрядам.
Псевдокод
LSD-сортировка
В качестве примера рассмотрим сортировку чисел. Как говорилось выше, в такой ситуации в качестве устойчивой сортировки применяют сортировку подсчетом, так как обычно количество различных значений разрядов не превосходит количества сортируемых элементов. Ниже приведен псевдокод цифровой сортировки, которой подается массив -разрядных чисел размера . Сам по себе алгоритм представляет собой цикл по номеру разряда, на каждой итерации которого элементы массива размещаются в нужном порядке во вспомогательном массиве . Для подсчета количества объектов, -й разряд которых одинаковый, а затем и для определения положения объектов в массиве используется вспомогательный массив . Функция возвращает -й разряд числа . Также считаем, что значения разрядов меньше .
function radixSort(int[] A)
for i = 1 to m
for j = 0 to k - 1
C[j] = 0
for j = 0 to n - 1
d = digit(A[j], i)
C[d]++
count = 0
for j = 0 to k - 1
tmp = C[j]
C[j] = count
count += tmp
for j = 0 to n - 1
d = digit(A[j], i)
B[C[d]] = A[j]
C[d]++
A = B
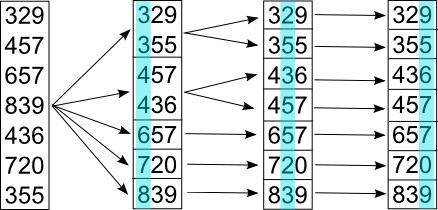
MSD-сортировка
Будем считать, что у всех элементов одинаковое число разрядов. Если это не так, то положим на более старших разрядах элементы с самым маленьким значением — для чисел это 0. Сначала исходный массив делится на частей, где — основание, выбранное для представления сортируемых объектов. Эти части принято называть "корзинами" или "карманами". В первую корзину попадают элементы, у которых старший разряд с номером имеет значение . Во вторую корзину попадают элементы, у которых старший разряд с номером имеет значение и так далее. Затем элементы, попавшие в разные корзины, подвергаются рекурсивному разделению по следующему разряду с номером . Рекурсивный процесс разделения продолжается, пока не будут перебраны все разряды сортируемых объектов и пока размер корзины больше единицы. (то есть останавливаемся когда или , где m — максимальное число разрядов в сортируемых объектах, , — левая и правая границы отрезка массива ).
В основу распределения элементов по корзинам положен метод распределяющего подсчета элементов с одинаковыми значениями в сортируемом разряде. Для этого выполняется просмотр массива и подсчет количества элементов с различными значениями в сортируемом разряде. Эти счетчики фиксируются во вспомогательном массиве счетчиков . Затем счетчики используются для вычисления размеров корзин и определения границ разделения массива. В соответствии с этими границами сортируемые объекты переносятся во вспомогательный массив , в котором размещены корзины. После того как корзины сформированы, содержимое вспомогательного массива переносится обратно в исходный массив и выполняется рекурсивное разделение новых частей по следующему разряду в пределах границ корзин, полученных на предыдущем шаге.
Изначально запускаем функцию так
function radixSort(int[] A, int l, int r, int d)
if d > m or l >= r
return
for j = 0 to k + 1
cnt[j] = 0
for i = l to r
j = digit(A[i], d)
cnt[j + 1]++
for j = 2 to k
cnt[j] += cnt[j - 1]
for i = l to r
j = digit(A[i], d)
c[l + cnt[j]] = A[i]
cnt[j]++
for i = l to r
A[i] = c[i]
radixSort(A, l, l + cnt[0] - 1, d + 1)
for i = 1 to k
radixSort(A, l + cnt[i - 1], l + cnt[i] - 1, d + 1)
Сложность
Пусть — количество разрядов, — количество объектов, которые нужно отсортировать, — время работы устойчивой сортировки. Цифровая сортировка выполняет итераций, на каждой из которой выполняется устойчивая сортировка и не более других операций. Следовательно время работы цифровой сортировки — .
Рассмотрим отдельно случай сортировки чисел. Пусть в качестве аргумента сортировке передается массив, в котором содержатся -значных чисел, и каждая цифра может принимать значения от до . Тогда цифровая сортировка позволяет отсортировать данный массив за время , если устойчивая сортировка имеет время работы . Если небольшое, то оптимально выбирать в качестве устойчивой сортировки сортировку подсчетом.
Если количество разрядов — константа, а , то сложность цифровой сортировки составляет , то есть она линейно зависит от количества сортируемых чисел.
Сложность MSD-сортировки оценивается величиной . При больших k величина становится малой и сложность становится линейной функцией
Существует так же модификация MSD-сортировки, при которой рекурсивный процесс останавливается при небольших размерах текущего кармана и вызывается более быстрая сортировка основанная на сравнениях (например, сортировка вставками).
Таким образом, если k небольшое, то лучше использовать LSD-сортировку, при больших k — MSD-сортировку.
Источники информации
- Дональд Кнут Искусство программирования, том 3. Сортировка и поиск
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ
- Визуализатор 1 — Java-аплет.
- Визуализатор 2 — Java-аплет.