Динамическое программирование по профилю

Определение:

Динамическое программирование по профилю (англ. dynamic programming with profile) — способ оптимизации перебора количества вариантов с помощью динамического программирования, когда одно из измерений не большое.

Определение:

Профиль (англ. profile) — один из столбцов (строк), удовлетворяющий условию задачи. Обычно используется в качестве состояния динамики.

Общие принципы

Обычно дана таблица и надо посчитать количество замощений этой таблицы некоторыми фигурами (замощение шахматной доски доминошками). Можно перебрать все варианты и выбрать из них удовлетворяющие условию. Но можно воспользоваться методом динамического программирования по профилю и сократить время по одной размерности до линейной. Затем пусть у нас есть правило по которому надо заполнить и для него нам надо [math]k[/math] предыдущих линий. Тогда можно перебрать все замощения длиной [math]k\times n[/math]. В итоге нужно заполнить данную таблицу этими замощениями. Получается, что если перебирать все варианты нам понадобиться [math]O(a^{nm})[/math] времени, а если перебирать только состояния и переходить по ним нам потребуется [math]O(a^{kn} \cdot m)[/math] времени (где [math]a[/math] - количество способов замещения [math]1[/math] клетки).

Задача о замощении домино

Условие

Найти количество способов замостить таблицу [math]n\times m[/math] с помощью доминошек размерами [math]1\times 2,2\times 1[/math].

Решение

Для удобства можно хранить профили в виде двоичных масок. В качестве состояния динамики будем использовать профили размерами [math]n[/math]. В этом профиле [math]1[/math] будет означать, что домино лежит горизонтально и заканчивается на этом столбце, иначе [math]0[/math]. Таких профилей будет [math]2^n[/math]. Теперь проверим из какого профиля в какой можно перейти.

Переходы (1-правильный переход, 2,3-неправильные)

Из профиля [math]i[/math] в профиль [math]j[/math] можно перейти если выполняются условия:

• Можно положить горизонтальные домино. То есть там где в [math]j[/math] профиле стоит [math]1[/math], в [math]i[/math] профиле должен стоять [math]0[/math].

• Можно доложить в оставшиеся клетки вертикальные домино. То есть оставшиеся [math]0[/math] в [math]i[/math] профиле должны образовывать четные подстроки.

Пусть [math]d[i][j] = 1[/math] если из профиля [math]i[/math] можно перейти в [math]j[/math]-ый, иначе [math]0[/math].

Пусть так же [math]a[k][i][/math] — количество способов замощения первых [math]k-1[/math] столбцов и заканчивавшийся на [math]i[/math]-ом профиле. Тогда [math]a[k][i]=\displaystyle \sum_{j=0}^{2^n -1} a[k-1][j]\cdot d[j][i][/math]

Ответом будет [math] \sum a[m][i][/math], где [math]i[/math] — профиль, который может быть последним (т.е. все группы из [math]0[/math] имеют четные размеры)

Реализация

// n, m - размер таблицы  
for [math]i = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
    for [math]j = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
        if можно перейти из [math]i[/math] в [math]j[/math] профиль 
            [math]\mathtt{d}[i][j] = \mathtt{1}[/math]
	else 
	    [math]\mathtt{d}[i][j] = \mathtt{0}[/math]
[math]\mathtt{a}[\mathtt{0}][\mathtt{0}] = \mathtt{1}[/math] // Так как мы можем начать только с профиля где все клетки 0  
for [math]k = \mathtt{1}..m - \mathtt{1} [/math]
    for [math]i = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
        for [math]j = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
	    [math]\mathtt{a}[k][i] = \mathtt{a}[k][i] + \mathtt{a}[k - \mathtt{1}][j]  \cdot  \mathtt{d}[j][i][/math]
[math]ans = \mathtt{0}[/math]
for [math]i = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
    if можно закончить [math]i[/math] профилем
        [math]ans = ans + \mathtt{a}[m - \mathtt{1}][i][/math]
return [math]ans[/math]

Оценка сложности: подсчет [math]d - 2^{2n}[/math] , и подсчет [math]a - 2^{2n}\times m[/math] в итоге [math]O(2^{2n}\times m)[/math]

Оценка памяти: [math]O(2^{2n}+2^{2n}\times m)[/math], так же можно заметить что в массиве [math]a[/math] для [math]k[/math] состояния нам нужно только [math]k-1[/math] состояние, при такой реализации нужно будет [math]O(2^{2n})[/math]. Еще можно не считать массив [math]d[/math], а просто каждый раз перепроверять можем ли мы перейти в это состояние в итоге потребуется [math]O(2\times 2^n)[/math] памяти, но нам потребуется больше времени [math]2^{2n}\times m\times f(i,j)[/math], где [math]f(i,j)[/math] время проверки возможности перехода из [math]i[/math] в [math]j[/math] равно [math]n[/math] и тогда время получается [math]O(2^{2n}\times m\times n)[/math].

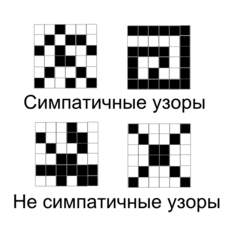
Задача о симпатичных узорах

Условие

Дана таблица [math]n\times m[/math], каждая клетка которой может быть окрашена в один из двух цветов: белый или черный. Симпатичным узором называется такая раскраска, при которой не существует квадрата [math]2\times 2[/math], в котором все клетки одного цвета. Требуется найти количество симпатичных узоров для соответствующей таблицы.

Решение

Для удобства можно хранить профиля в виде двоичных масок. В качестве состояния динамики будем использовать профили размера [math]n[/math]. В этом профиле [math]1[/math] будет означать что клетка закрашена в черный цвет, и [math]0[/math] если в белый. Из профиля [math]i[/math] в [math]j[/math]-ый можно перейти если выполнено условие:

• если поставить [math]i[/math] и [math]j[/math] профиль рядом, то не должно быть квадратов [math]2\times 2[/math] одного цвета

Пусть [math]d[i][j] = 1[/math] если из профиля [math]i[/math] можно перейти в [math]j[/math]-ый, иначе [math]0[/math].

Пусть так же [math]a[k][i][/math] — количество способов раскрашивания первые [math]k-1[/math] столбцов и заканчивавшийся на [math]i[/math]-ом профиле. Тогда [math]a[k][i]=\displaystyle \sum_{j=0}^{2^n -1} a[k-1][j]\cdot d[j][i][/math]

Ответом будет [math] \displaystyle \sum_{j=0}^{2^n -1} a[m][i][/math]

Реализация

// n, m - размер таблицы   
for [math]i = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
    for [math]j = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
        if можно перейти из [math]i[/math] в [math]j[/math] профиль 
            [math]\mathtt{d}[i][j]\ =\ \mathtt{1}[/math]
	else
	    [math]\mathtt{d}[i][j]\ =\ \mathtt{0}[/math]
for [math]i = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
    [math]\mathtt{a}[i][0]\ = \mathtt{1}[/math] // Так как мы можем начать c любого профиля
for [math]k = \mathtt{1}..m - \mathtt{1} [/math]
    for  [math]i = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
        for [math]j = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
	     [math]\mathtt{a}[k][i] = \mathtt{a}[k][i] + \mathtt{a}[k - 1][j] \cdot \mathtt{d}[j][i][/math]  
[math]ans = \mathtt{0}[/math]
for [math]i = \mathtt{0}..(\mathtt{1}\lt \lt n) - \mathtt{1}[/math]
    [math]ans = ans + a[m - \mathtt{1}][i][/math] // Так как мы можем закончить любым профилем 
return [math]ans[/math]

Оценка сложности: подсчет [math]d - 2^{2n}[/math] , и подсчет [math]a - 2^{2n}\times m[/math] в итоге [math]O(2^{2n}\times m)[/math]

Оценка памяти: [math]O(2^{2n}+2^{2n}\times m)[/math], так же можно заметить что в массиве [math]a[/math] для [math]k[/math] состояния нам нужно только [math]k-1[/math] состояние, при такой реализации нужно будет [math]O(2^{2n})[/math]. Еще можно не считать массив [math]d[/math], а просто каждый раз перепроверять можем ли мы перейти в это состояние в итоге потребуется [math]O(2\times 2^n)[/math] памяти, но нам потребуется больше времени [math]2^{2n}\times m\times f(i,j)[/math], где [math]f(i,j)[/math] время проверки возможности перехода из [math]i[/math] в [math]j[/math] равно [math]n[/math] и тогда время получается [math]O(2^{2n}\times m\times n)[/math].

Динамика по изломанному профилю

Определение:

Изломанный профиль (англ. broken profile) — обобщение прямого профиля на случай, когда обработанным является не целое число столбцов, а некоторое количество столбцов и несколько первых клеток следующего столбца.

Это очень сильная оптимизация динамики по профилю. Идея в том, чтобы добиться как можно меньшего числа переходов (от одного профиля к другому). Теперь профиль — это не только маска, но ещё и место излома. Выглядит это так:

Пример

Еще раз используем в качестве примера задачу о замощении. Базовая линия теперь будет ломаной: при прохождении через [math]i[/math]-ю горизонталь сверху вниз, она переходит на предыдущую вертикаль и спускается до низу.

Профилем будет пара [math](p, i)[/math], в [math]p[/math] будет информация о [math]n + 1[/math] маленьком квадратике слева от базовой линии, имеющем с ней общие точки; [math]i[/math] обозначает номер горизонтали, на которой произошел излом. Квадратики профиля будут нумероваться сверху вниз, так что угловой будет иметь номер [math]i + 1[/math]. Горизонтали будем нумеровать с нуля, так что [math]i[/math] пробегает значения от [math]0[/math] до [math]n - 1[/math].

Пусть [math]d[i][j] = 1[/math] если из профиля [math]pr_1[/math] = [math](p_1, i_1)[/math] можно перейти в [math]pr_2 = (p_2, i_2)[/math], иначе [math]0[/math].

• Eсли [math]i \lt n - 1[/math], то [math]i_1 + 1 = i_2[/math], иначе [math]i_2 = 0 [/math];

• Mожно так положить доминошку, накрывающую квадратик с номером [math]i + 1[/math], что после этого в [math]p_2[/math] будет храниться в точности информация о соответствующих квадратиках.

Проще говоря, доминошку можно класть только двумя способами — как показано на рисунках (на квадратик с номером [math]i + 1[/math] можно положить не более одной вертикальной и горизонтальной доминошки). То, что потом получается после сдвига вниз излома, и будет новым профилем. Заметим, что если клетка [math]i + 1[/math] занята, то доминошку уже не надо класть, и [math](p, i)[/math] логично отождествить с [math](p, i + 1)[/math]. Условно пишется — "[math]i + 1[/math]", однако, нужно всегда иметь в виду возможность [math]i = n - 1[/math].

Легко заметить, что количество профилей увеличилось в [math]2n[/math] раз (добавилось число от [math]1[/math] до [math]n[/math] и еще один бит). Но зато количество переходов резко сократилось с [math]2^n[/math] до [math]2[/math].

//Для профиля (p, i) выводятся все переходы из него (нумерация горизонталей начинается с нуля и i = 0..n - 1)
// Функция bit(x,i), возвращающая единицу или ноль или i-й бит в двоичной записи числа x
print_all_links([math]p[/math], [math]i[/math]):
    if [math]\mathtt{bit}(\mathtt{p, i + 1}) = \mathtt{0}[/math]
        if [math]i = n - 1[/math]
            println [math]((p - (2 \lt \lt  i)) \lt \lt  1[/math], " ", [math]0)[/math]
        else
            println [math](p - (2 \lt \lt  i)[/math], " ", [math]i + 1)[/math]
    else 
        if [math]\mathtt{bit}(\mathtt{p, i}) = \mathtt{0}[/math]
            if [math]i = n - 1 [/math]
               println [math]((p\lt \lt  1)[/math], " ", [math]0)[/math]
            else   
               println [math](p + (1 \lt \lt  i)[/math], " ", [math](i + 1) % n)[/math]
    if [math]i \lt  n - 1[/math] && [math]\mathtt{bit}(\mathtt{p, i + 2}) = \mathtt{0}[/math]
            println [math](p + (4 \lt \lt  i)[/math], " ", [math]i + 1)[/math]

При такой реализации существует немало профилей только с одним переходом (например, у которых [math](i + 1)[/math]-й бит равен единице).

Отождествим все профили с один переходом с теми, кто их них получается. Это будет выглядеть так: пусть pr2 (и только он) получается из pr1, который, в свою очередь, получается из pr0. Тогда имеются такие соотношения: d[pr0, pr1]=1, d[pr1, pr2]=1. Отождествить pr1 и pr2 -- это, по сути, заменить эти два соотношение на одно, то есть теперь d[pr0, pr1]=0 и d[pr1, pr2]=0, но d[pr0, pr2]=1, и так далее.

Таким образом, возможно сокращение профилей не менее чем вдвое. Дальнейшие оптимизации мы оставляем читателю.

В итоге получаем асимптотику 2nn (количество переходов, то есть время на вычисление a[i]) умножить на m равно O(2nnm). Она значительно лучше всего, что мы получали до сих пор, и это серьезный повод использовать изломанный профиль вместо обычного.

См. также

• Динамическое программирование

Источники информации

• Динамическое программирование по профилю