Специальные формы КНФ — различия между версиями
(→КНФ в форме Крома) |
Nemzs (обсуждение | вклад) (→КНФ в форме Хорна) |
||
| Строка 36: | Строка 36: | ||
|statement= Существует алгоритм, который за полиномиальное время проверяет, что функцию, заданную в форме Хорна можно удовлетворить. | |statement= Существует алгоритм, который за полиномиальное время проверяет, что функцию, заданную в форме Хорна можно удовлетворить. | ||
|proof= Далее будет приведено доказательство, предлагающее алгоритм решения. | |proof= Далее будет приведено доказательство, предлагающее алгоритм решения. | ||
| + | *'''Представление функции''' | ||
| + | |||
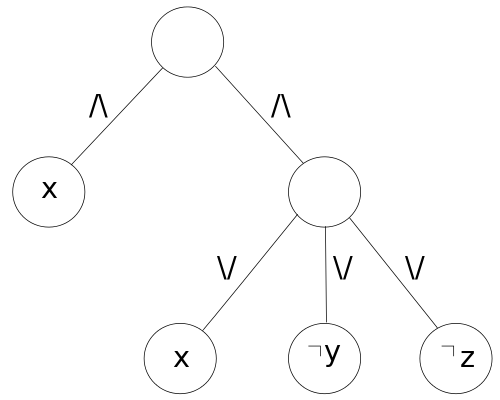
| + | Функцию можно представить в любом виде. Например, можно использовать древовидную структуру. Для формулы <tex> x \wedge (x \vee \neg y \vee \neg z) </tex>, которую мы будем использовать далее, дерево может выглядеть так : | ||
| + | [[Файл:Tree_structure.png]] | ||
| + | |||
*'''Шаг 1. Одиночное вхождение переменных''' | *'''Шаг 1. Одиночное вхождение переменных''' | ||
| Строка 43: | Строка 48: | ||
*'''Шаг 2.''' Идем по скобкам и выписываем все встречающиеся нам переменные, кроме тех, с которыми мы работали на предыдущем шаге. Если переменная всегда входит без отрицаний, присваиваем ей значение <tex>1</tex>, если переменная всегда входит с отрицаниями, присваиваем <tex>0</tex>. На данном шаге никакая скобка не может обратиться в <tex>0</tex>. | *'''Шаг 2.''' Идем по скобкам и выписываем все встречающиеся нам переменные, кроме тех, с которыми мы работали на предыдущем шаге. Если переменная всегда входит без отрицаний, присваиваем ей значение <tex>1</tex>, если переменная всегда входит с отрицаниями, присваиваем <tex>0</tex>. На данном шаге никакая скобка не может обратиться в <tex>0</tex>. | ||
| − | *'''Шаг 3.''' | + | *'''Шаг 3.''' Опустим одиночно стоящие переменные и скобки, в которых значение стало равным 1, так как они уже не влияют на существование ответа. Проделаем с полученным выражением алгоритм, начиная с <tex>1</tex> шага, пока <tex>1</tex> шаг не найдёт ответ. |
*Время работы алгоритма: | *Время работы алгоритма: | ||
| + | Так как функция состоит из простых выражений, мы сможем её разбить на дерево за линейное время. | ||
Будем считать, что длиной формулы является количество переменных, входящих в нее. Обозначим ее за <tex> n </tex>. | Будем считать, что длиной формулы является количество переменных, входящих в нее. Обозначим ее за <tex> n </tex>. | ||
| − | В каждом шаге мы | + | В каждом шаге алгоритма мы обрабатываем очередную одиночную переменную за линейное время. Отсюда следует, что время работы линейное, относительно количества входящих переменных. |
}} | }} | ||
{{Утверждение | {{Утверждение | ||
Версия 23:46, 16 июня 2016
Рассмотрим две формы, с помощью которых можно представить формулы, заданные в конъюнктивной нормальной форме, то есть имеющей вид конъюнкции выражений в скобках, каждое из которых представляет собой дизъюнкцию одного или нескольких литералов. Эти две формы интересны тем, что для них существует алгоритм, который может за полиномиальное время проверить, существует ли набор аргументов, на которых данная функция будет принимать значение , в то время, как для обычной функции, не представленной данной формой, эта задача является NP-полной.
Содержание
КНФ в форме Крома
| Определение: |
| Конъюнктивная нормальная форма (КНФ) в форме Крома (2-КНФ) (англ. 2-CNF) — это конъюнкция выражений в скобках, каждое из которых представляет собой дизъюнкцию нескольких литералов, количество которых не превышает двух. |
Пример :
Разрешимать булевой формулы, заданой в форме Крома
| Утверждение: |
Функцию можно задать в форме Крома выполнено следующее следствие: |
КНФ в форме Хорна
| Определение: |
| Конъюнктивная нормальная форма (КНФ)в форме Хорна (англ. Horn clause) — это конъюнкция выражений в скобках, каждое из которых представляет собой дизъюнкцию литералов, в которой присутствует не более одного литерала без отрицания. |
Пример:
Каждая скобка представляет собой Дизъюнкт Хорна[1].
Любую формулу можно представить в виде КНФ в форме Хорна. Для этого формулу необходимо преобразовать в конъюнкцию элементарных дизъюнкций и далее каждую дизъюнкцию представить в форме дизьюнкта Хорна.
| Утверждение: |
Функцию можно задать в форме Хорна выполнено следующее следствие: |