|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| − |
| |
| | | | |
| | | | |
Определения
| Определение: |
| Контекстно-свободная грамматика [math] G = \langle N, \Sigma, P, S \rangle[/math] называется самоприменимой (англ. self-embeded), если [math] \exists A \in N: A \Rightarrow^* \alpha A \beta[/math], [math] \alpha \neq \varepsilon \land \beta \neq \varepsilon [/math] . |
| Определение: |
| Нетерминал [math] A \in N[/math] в грамматике [math] G = \langle N, \Sigma, P, S \rangle[/math] называется рекурсивным (англ. recursive), если [math] \exists \alpha,\beta \in (\Sigma \cup N)^* : A \Rightarrow^* \alpha A \beta[/math] . |
| Определение: |
| Нетерминалы [math] A,B \in N[/math] в грамматике [math] G = \langle N, \Sigma, P, S \rangle[/math] называются взаимно рекурсивными (англ. mutual recursive), если [math] \exists \alpha_1,\beta_1,\alpha_2,\beta_2 \in (\Sigma \cup N)^* : A \Rightarrow^* \alpha_1 B \beta_1 \land B \Rightarrow^* \alpha_2 A \beta_2[/math] . |
Алгоритм преобразования грамматики в конечный автомат
| Лемма: |
Не самоприменимая контекстно-свободная грамматика генерирует регулярный язык. |
| Доказательство: |
| [math]\triangleright[/math] |
|
В качестве конструктивного доказательства рассмотрим алгоритм построения конечного автомата по грамматике. Также приведем ссылку на формальное доказательство[1]. |
| [math]\triangleleft[/math] |
Идея алгоритма
Пусть, [math] N^* [/math] множество рекурсивных нетерминалов из [math] N [/math].
Пусть, [math] P = \{N_1,N_2,\ldots,N_K\} [/math] разбиение [math] N^*[/math] на [math] k [/math] дизъюнктных множеств взаимно рекурсивных нетерминалов,
[math] N_1 \cup N_2 \cup \ldots \cup N_k = N^* \land \forall i[/math] [math] N_i \neq \emptyset [/math].
Определим вспомогательную функцию [math]\mathtt {isLeftType}(N_i)[/math], которая возвращает [math]true[/math], если существует [math] (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \alpha \neq \varepsilon ][/math].
Аналогично определим функцию [math]\mathtt {isRightType}(N_i)[/math], которая возвращает [math]true[/math], если существует [math] (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \beta \neq \varepsilon ][/math]
bool isLeftType([math]N_i[/math]: nonterminal):
return [math] \exists (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \alpha \neq \varepsilon ][/math]
bool isRightType([math]N_i[/math]: nonterminal):
return [math] \exists (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \beta \neq \varepsilon ][/math]
Будем называть [math]\mathtt {typeRecursive}[/math] набор четырех величин [math]\{left, right, self, cycle\} [/math]
Определим функцию [math]\mathtt {getTheTypeOfMutualRecursiveSet}(N_i): P \rightarrow \mathtt {typeRecursive} [/math]:
function getTheTypeOfMutualRecursiveSet([math]N_i[/math]: nonterminal): typeRecurcive
if !isLeftType([math]N_i[/math]) and isRightType([math]N_i[/math])
return left
if isLeftType([math]N_i[/math]) and !isRightType([math]N_i[/math])
return right
if isLeftType([math]N_i[/math]) and isRightType([math]N_i[/math])
return self
if !isLeftType([math]N_i[/math]) and !isRightType([math]N_i[/math])
return cyclic
- Состояние [math] left[/math] означает, что [math] N_i [/math] состоит только из лево-рекурсивных нетерминалов.
- Состояние [math] right[/math] означает, что [math] N_i [/math] состоит только из право-рекурсивных нетерминалов.
- Состояние [math] cyclic[/math] означает, что [math] N_i [/math] состоит только из правил, участвующих в рекурсии.
- Состояние [math] self[/math] означает, что [math]i [/math] такое, при котором грамматика самоприменима.
Заметим, что [math] \forall i [/math] [math]\mathtt {getTheTypeOfMutualRecursiveSet}(N_i) \neq self [/math], т.к в противном случае грамматика будет самоприменима.
В основе алгоритма будет рекурсивный обход грамматики. Спускаемся по грамматике до тех пор не приходим в нетерминал или символ алфавита:
- Символ алфавит или [math] \varepsilon [/math] — добавляем новое правило в автомат;
- Нерекурсивный нетерминал — запускаемся от всех правых частей правил, который терминал порождает;
- Рекурсивный нетерминал — в зависимости от типа рекурсивного нетерминала, продолжаем рекурсию (будет ясно из пседокода).
Псевдокод
[math]Q[/math] — множество состояний ДКА.
[math]\Delta[/math] — множество переходов ДКА.
[math]T[/math] — множество допускающих состояний.
function createFA(G: grammar): Automaton // [math] G = \langle N, \Sigma, P, S \rangle[/math]
[math]\mathtt{Q} \leftarrow \varnothing[/math]
[math]\Delta \leftarrow \varnothing [/math]
s = createState() // createState создает некоторый объект, не принадлежащий [math]Q[/math], возвращает этот объект и добавляет его в [math]Q[/math]
f = createState()
[math]F \leftarrow \{f\} [/math]
return makeFA(s,S,f)
function makeFA(q0: vertex, a: char, q1: vertex): Automaton
if a == [math] \varepsilon [/math] or a [math] \in \Sigma[/math] // пришли в лист дерева разбора
[math] \Delta = \Delta \cup \{(q_0,a,q_1)\} [/math]
return
if a == [math]X\beta[/math] where [math] X \in (N \cup \Sigma) \land \beta \in (N \cup \Sigma)^* \land |\beta| \gt 0 [/math]
q = createState()
makeFA([math]q_0,X,q_1[/math])
makeFA([math]q, \beta, q_1 [/math])
return
if exist [math] N_i [/math] where [math] a \in N_i [/math]
foreach b in [math]N_i[/math]
[math]q_b[/math] = createState
if getTheTypeOfMutualRecursiveSet([math] N_i [/math]) == left
foreach C in [math]N_i[/math] where [math] C \rightarrow X_1 \ldots X_m \land X_1, \ldots X_m \neq N_i [/math]
makeFA([math]q_0, X_1 \ldots X_m, q_C[/math])
foreach C,D in [math]N_i[/math] where [math] C \rightarrow DX_1 \ldots X_m \land X_1, \ldots X_m \neq N_i [/math]
makeFA([math]q_D, X_1 \ldots X_m, q_C[/math])
[math] \Delta = \Delta \cup \{(q_a,\varepsilon,q_1)\} [/math]
else // рекурсивный нетерминал right или cyclic
foreach C in [math]N_i[/math] where [math] C \rightarrow X_1 \ldots X_m \land X_1, \ldots X_m \neq N_i [/math]
makeFA([math]q_C, X_1 \ldots X_m, q_1[/math])
foreach C,D in [math]N_i[/math] where [math] C \rightarrow DX_1 \ldots X_m \land X_1, \ldots X_m \neq N_i [/math]
makeFA([math]q_D, X_1 \ldots X_m, q_C[/math])
[math] \Delta = \Delta \cup \{(q_0, \varepsilon ,q_a)\} [/math]
return
foreach p in [math]P[/math] where p == [math] a \rightarrow \beta [/math]
makeFA([math] q_0, \beta, q_1 [/math])
Аппроксимации самоприменимой грамматики
В данном разделе покажем методы апроксимации: [math]\mathrm {RTN}[/math] (recursive transition network) аппроксимацию и [math]\mathrm {MN}[/math] (Mohri and Nederhof's) аппроксимацию — самоприменимой контекстно-свободной грамматики [math] G = \langle N, \Sigma, P, S \rangle[/math] к регулярной грамматике. Для удобства будем считать, что грамматика представлена в НФХ.
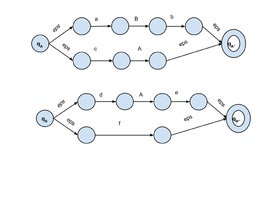
Автоматы
[math]T_A,T_B[/math] для грамматики
[math]A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f [/math]RTN аппроксимация
Построим, по данной грамматике аппроксимирующий ее конечный автомат.
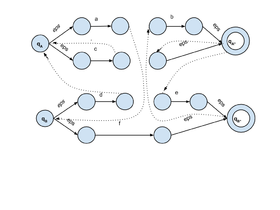
Конечный автомат для грамматики
[math]A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f [/math]- Для каждого нетерминала [math] A[/math] в грамматике, создадим новый конечный автомат [math] T_A[/math], добавим в него два состояния [math] q_A[/math] и [math]q_{A^*}[/math].
- Для каждого правила грамматике [math] (A \rightarrow X_1 \ldots X_m ) \in P[/math], введм новые состояния в автомат этого нетерминала [math] q_0^A \ldots q_m^A[/math], а также добавим новые правила перехода в [math] \Delta[/math]: [math] (q_A, \varepsilon, q_0),(q_0^A,X_1,q_1^A), \ldots,(q_{m-1}^A,X_m,q_m^A),(q_m^A,\varepsilon,q_{A^*})[/math].
- Таким образом мы построили множество конечных автоматов [math]T[/math] = [math] \{ T_A \mid A \in N\}[/math] для каждого нетерминала [math]A[/math]. Теперь объединим все в один автомат. Объединим все состоянии автоматов из [math]T[/math] в множество [math]Q[/math]. Скопируем все переходы каждого автомата из [math]T[/math] в [math]\Delta[/math]. Далее для каждого перехода вида [math](q,A,p), A\in N[/math], вместо него добавим два новых перехода: [math] (q, \varepsilon, q_A),(q_A^{*}, \varepsilon, p) [/math].
MN аппроксимация
Построим по данной самоприменимой контекстно-свободной грамматике [math] G [/math] регулярную грамматику [math] G^*[/math].
- Для каждого нетерминала [math] A \in N [/math] из [math]G[/math], добавим нетерминалы [math]A[/math] и [math] A^*[/math] в [math] G^* [/math].
- Для каждого правила [math] A \rightarrow {\alpha}_{0} B_1 {\alpha}_{1} B_2 {\alpha}_{2} \ldots B_m {\alpha}_{m}[/math], где [math] B_1, \ldots, B_m \in N \land {\alpha}_i \in \Sigma^*[/math]. Добавим в [math] G^*[/math] нетерминалы [math] B_1 \ldots B_m , B_1^* \ldots B_m^*[/math] и следуюшие правила: [math]\begin{cases} A \rightarrow {\alpha}_0 B_1 \\ B_1^* \rightarrow {\alpha}_1 B_2\\ \ldots \\ B^*_m \rightarrow {\alpha}_m A^* \end{cases}[/math].
- (Если [math]m = 0 [/math], тогда добавим правило [math] A \rightarrow {\alpha}_0 A^* [/math]).
В итоге [math] G^*[/math] — правоконтекстная грамматика, эквивалентная конечному автомату, который задает регулярный язык.
Пример
[math] G = \begin{cases} A \rightarrow \alpha B \alpha
\\ B \rightarrow \beta A | \beta
\end{cases}\Rightarrow
G^* = \begin{cases} A \rightarrow \alpha B
\\ A^* \rightarrow B^* | \varepsilon
\\ B \rightarrow \beta A | \beta B^*
\\ B^* \rightarrow \alpha A^* | \varepsilon
\end{cases}[/math]
Исходная грамматика [math] G [/math] генерирует язык: [math] \{(ab)^n a^n \mid n \gt 0\}[/math]. Результирущая грамматика [math] G^*[/math] генирирует регулярный язык: [math] (ab)^+ a^*[/math].
Сравнение двух методов
Ясно, что оба языка, генерируемых конечным автомат для первого метода и апрокисимируещей граматикой для второго метода, содержат в себе язык генерируемый исходной грамматикой.
Привлекателным свойством [math]\mathrm {MN}[/math] аппроксимации по сравнению с [math]\mathrm {RTN}[/math], то, что она можеть быть применима к большим грамматикам: для каждого нетерминала грамматике [math] G[/math], добавляется не более одного нового нетерминала в [math] G^*[/math] и размер результирующий грамматики максимум в [math]2[/math] раза больше, чем размер исходной. Так как для [math]\mathrm {RTN}[/math] апроксимации грамматики [math] G = \langle N, \Sigma, P, S \rangle[/math], количество состаяний апроксимируещего автомата в худшем случаи может составлять [math] O(|N|^2)[/math], что может быть критично для аппроксимации больших грамматик.
Также,еще несколько эффекивных методов аппрокимации можно найти в статьях, приведенных в ссылках.
См. также
Примечания
Источники информации

