Динамическое программирование — различия между версиями
Borisov (обсуждение | вклад) |
Borisov (обсуждение | вклад) |
||
| Строка 4: | Строка 4: | ||
|definition = '''Принцип оптимальности для подзадач''' – важнейшее свойство задачи, формулирующееся следующим образом: <br> «Если есть оптимальное решение для некоторой подзадачи, которая возникает в процессе решения задачи, <br>то именно его нужно использовать для решения задачи в целом»}}<br> | |definition = '''Принцип оптимальности для подзадач''' – важнейшее свойство задачи, формулирующееся следующим образом: <br> «Если есть оптимальное решение для некоторой подзадачи, которая возникает в процессе решения задачи, <br>то именно его нужно использовать для решения задачи в целом»}}<br> | ||
Рассмотрим принцип оптимальности для динамического программирования на префиксе:<br> | Рассмотрим принцип оптимальности для динамического программирования на префиксе:<br> | ||
| + | [[Файл:ST.jpg]] | ||
| + | |||
Префикс оптимального пути из $S \rightsquigarrow U$ является оптимальным путём из $S \rightsquigarrow U$. | Префикс оптимального пути из $S \rightsquigarrow U$ является оптимальным путём из $S \rightsquigarrow U$. | ||
| − | Требуется дойти до $T$. Оптимальный путь проходит через $U$. | + | Требуется дойти до $T$. Оптимальный путь проходит через $U$. |
| + | Пусть префикс $dU$ неоптимальный. Это значит, что есть более оптимальный путь. Тогда заменим этот префикс на более оптимальный путь до $U$, | ||
| + | а путь от $U \rightsquigarrow T$ добавим в конец. Получится более оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется. | ||
</wikitex> | </wikitex> | ||
| − | == | + | ==Ссылки== |
*Лекция 10.11.2011 | *Лекция 10.11.2011 | ||
| − | *[http://ru.wikipedia.org/wiki/%D0%96%D0%B0%D0%B4%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC#.D0.9E.D0.BF.D1.82.D0.B8.D0.BC.D0.B0.D0.BB.D1.8C.D0.BD.D0.BE.D1.81.D1.82.D1.8C_.D0.B4.D0.BB.D1.8F_.D0.BF.D0.BE.D0.B4.D0.B7.D0.B0.D0.B4.D0.B0.D1.87|Википедия, | + | *[http://ru.wikipedia.org/wiki/%D0%96%D0%B0%D0%B4%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC#.D0.9E.D0.BF.D1.82.D0.B8.D0.BC.D0.B0.D0.BB.D1.8C.D0.BD.D0.BE.D1.81.D1.82.D1.8C_.D0.B4.D0.BB.D1.8F_.D0.BF.D0.BE.D0.B4.D0.B7.D0.B0.D0.B4.D0.B0.D1.87|Википедия, Жадный алгоритм] |
| + | *Т. Кормен. «Алгоритмы. Построение и анализ» (Глава 15.3) | ||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
[[Категория:Динамическое программирование]] | [[Категория:Динамическое программирование]] | ||
Версия 07:40, 23 ноября 2011
<wikitex>
Определение
| Определение: |
| Принцип оптимальности для подзадач – важнейшее свойство задачи, формулирующееся следующим образом: «Если есть оптимальное решение для некоторой подзадачи, которая возникает в процессе решения задачи, то именно его нужно использовать для решения задачи в целом» |
Рассмотрим принцип оптимальности для динамического программирования на префиксе:
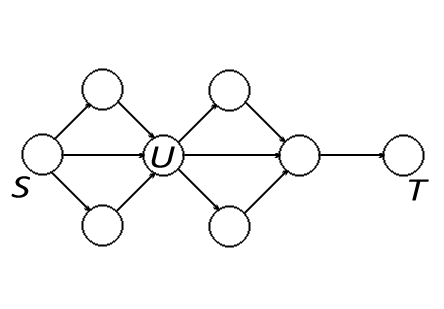
Префикс оптимального пути из $S \rightsquigarrow U$ является оптимальным путём из $S \rightsquigarrow U$. Требуется дойти до $T$. Оптимальный путь проходит через $U$. Пусть префикс $dU$ неоптимальный. Это значит, что есть более оптимальный путь. Тогда заменим этот префикс на более оптимальный путь до $U$,
а путь от $U \rightsquigarrow T$ добавим в конец. Получится более оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется.
</wikitex>
Ссылки
- Лекция 10.11.2011
- Жадный алгоритм
- Т. Кормен. «Алгоритмы. Построение и анализ» (Глава 15.3)