Теорема Редеи-Камиона — различия между версиями
| Строка 95: | Строка 95: | ||
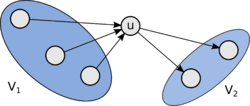
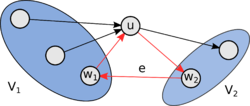
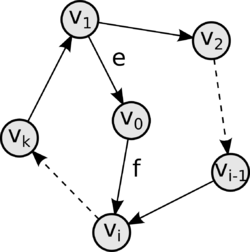
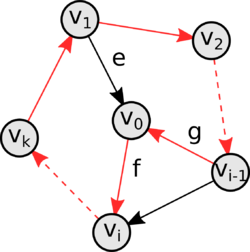
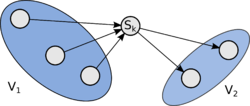
* <tex> V_2 = \{ u \in VT | u \notin S_k, f = (v_i, u) \in ET, \forall i = \overline{1, n} \} </tex>. | * <tex> V_2 = \{ u \in VT | u \notin S_k, f = (v_i, u) \in ET, \forall i = \overline{1, n} \} </tex>. | ||
Тогда <tex> V_1 \cap V_2 = \emptyset </tex>. | Тогда <tex> V_1 \cap V_2 = \emptyset </tex>. | ||
| + | [[Файл: Redei_kamion_9.png|250px|thumb|center]] | ||
| + | |||
Турнир сильно связен, следовательно: | Турнир сильно связен, следовательно: | ||
* <tex> V_1 \neq \emptyset </tex>, (иначе <tex> T </tex> не будет сильно связным, так как тогда нет простых путей с началом в <tex> V_2 </tex> и концом в <tex> {v_1, \ldots, v_k} </tex>) | * <tex> V_1 \neq \emptyset </tex>, (иначе <tex> T </tex> не будет сильно связным, так как тогда нет простых путей с началом в <tex> V_2 </tex> и концом в <tex> {v_1, \ldots, v_k} </tex>) | ||
Версия 20:06, 26 февраля 2012
| Теорема (Редеи-Камиона (для пути)): |
В любом турнире есть гамильтонов путь. |
| Доказательство: |
|
Приведем доказательство по индукции по числу вершин в графе. Пусть - количество вершин в графе. База индукции: Очевидно, для утверждение верно. Индукционный переход: Пусть предположение верно для всех турниров с количеством вершин не более . Рассмотрим турнир с вершинами. Пусть – произвольная вершина турнира . Тогда турнир имеет вершин, значит, в нем есть гамильтонов путь . Одно из ребер или обязательно содержится в . Если ребро , то путь - гамильтонов. Пусть теперь ребро - первая вершина пути , для которой ребро . Если такая вершина существует, то в существует ребро и путь – гамильтонов. Если такой вершины не существует, то путь - гамильтонов. Значит, в любом случае в турнире существует гамильтонов путь, q.e.d. |
| Теорема (Редеи-Камиона (для цикла)): | ||||||||||
В любом сильно связанном турнире есть гамильтонов цикл. | ||||||||||
| Доказательство: | ||||||||||
|
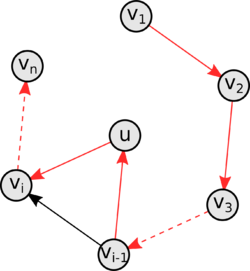
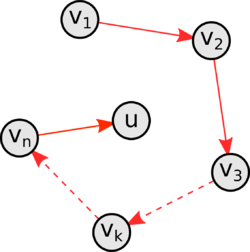
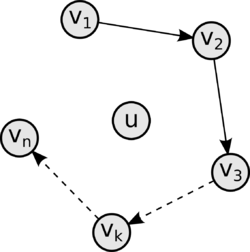
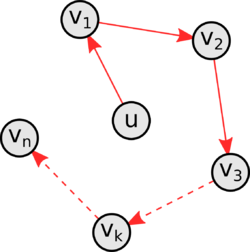
Приведем доказательство по индукции по числу вершин в цикле. Пусть - количество вершин в графе. База индукции:
Индукционный переход:
| ||||||||||
| Лемма (Следствие): |
Турнир является сильно связанным тогда и только тогда, когда он имеет гамильтонов цикл. |
См. также
Литература
- Асанов М., Баранский В., Расин В.: Дискретная математика: Графы, матроиды, алгоритмы
- Ф. Харари: Теория графов