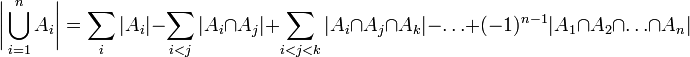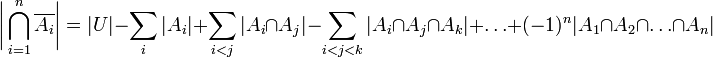Формула включения-исключения — различия между версиями
Павел (обсуждение | вклад) |
|||
| Строка 75: | Строка 75: | ||
}} | }} | ||
| − | == | + | == Беспорядки == |
| − | + | '''Беспорядком''' в комбинаторике называется перестановка чисел от <tex>1</tex> до <tex>n</tex>, в которой ни один элемент не стоит на своём месте. | |
| − | + | {{Теорема | |
| + | |id=идентификатор (необязательно), пример: th1. | ||
| − | [[Файл:Formula.png]] | + | |statement=Количество всех беспорядков порядка <tex>n</tex> или [http://ru.wikipedia.org/wiki/Субфакториал субфакториалом] числа <tex>n</tex> (обозначение: !<tex>n</tex>) может быть вычислено по формуле: [[Файл:Formula.png]] |
| − | + | |proof=}} | |
| − | '''Доказательство''' | + | '''Доказательство:''' |
| − | + | Воспользуемся принципом включения-исключения: обозначим за [[Файл:Formula4.png]] — количество перестановок из <tex>n</tex> элементов, в каждой из которых <tex>i</tex>-ый элемент стоит на своём месте. Тогда по формуле включения-исключения имеем: | |
| − | |||
1) [[Файл:Formula2.png]] | 1) [[Файл:Formula2.png]] | ||
| Строка 94: | Строка 94: | ||
2) [[Файл:Formula3.png]] | 2) [[Файл:Formula3.png]] | ||
| − | Данные формулы | + | Данные формулы являются эквивалентными. Действительно, если некоторое множество <math>\mathbf{S}</math> являются подмножествами некоторого множества [[Файл:Formula5.png]], то, в силу законов де Моргана |
| − | + | <tex>|</tex> <math>\mathbf{S}</math> <tex>|</tex> <tex>=</tex> <tex>|</tex> [[Файл:Formula5.png]] <tex>|</tex> — <tex>|</tex> <math>\lnot</math><math>\mathbf{S}</math> <tex>|</tex>. | |
| − | + | В данной задаче множество [[Файл:Formula5.png]] — есть количество перестановок из <tex>n</tex> элементов, т.е. <tex>n!</tex>. Верхнее подчеркивание или символ <math>\lnot</math> перед <math>\mathbf{S}</math> означает дополняющее множество до [[Файл:Formula5.png]] <math>\Rightarrow</math> <math>\lnot</math> [[Файл:Formula4.png]] — количество перестановок, где <tex>i</tex>-ый элемент стоит '''НЕ''' на своём <tex>i</tex>-ом месте. | |
| − | + | Таким образом величина в левой части формулы 2) — есть количество перестановок, где на 1-ой позици '''НЕ''' 1, на 2-ой позици '''НЕ''' 2 и т.д. То есть количество искомых беспорядков. Осталось определить величины в правой части: | |
| − | + | [[Файл:Formula5.png]] <tex>=</tex> <tex>n!</tex>. | |
| − | |||
| − | [[Файл: | + | |[[Файл:Formula4.png]]| — количество перестановок с уже занятой позицией <tex>i</tex> <math>\Rightarrow</math> |[[Файл:Formula4.png]]| <tex>=</tex> <tex>(n - 1)!</tex>. Суммирование ведется по всем <tex>i</tex> <math>\Rightarrow</math> <tex>\sum \limits_{i = 1}^{n} |\lnot </tex>[[Файл:Formula4.png]]<tex>|</tex> <tex>=</tex> <math>\binom{n}{1}</math><tex>\cdot</tex><tex>(n-1)!</tex> |
| − | + | Производя аналогичные рассуждения, получаем, что сумма пересечений некоторых <tex>k</tex> множеств (то есть сумма всеx перестановки при некоторых зафиксированных <tex>k</tex> позициях) — есть <tex>(n-k)!</tex>. Количество способов выбрать <tex>k</tex> позиций — <math>\binom{n}{k}</math> <math>\Rightarrow</math> Количество перестановок с <tex>k</tex> неподвижными точками: <math>\binom{n}{k}</math><tex>\cdot</tex><tex>(n-k)!</tex> | |
| + | |||
| + | [[Файл:Formula9.png]] <tex>=</tex> <tex>n!</tex> <tex>+</tex> <tex>\sum \limits_{i = 1}^{n} (-1)^{n}(n - k)!</tex><tex>\cdot</tex><math>\binom{n}{k}</math> | ||
| + | |||
| + | Раскрывая <math>\binom{n}{k}</math> по общеизвестной формуле, получим требуемое выражение, то есть количество беспорядков порядка <tex>n</tex>. | ||
| − | |||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Комбинаторика]] | [[Категория: Комбинаторика]] | ||
Версия 20:36, 15 декабря 2012
Формула включения-исключения — комбинаторная формула, выражающая мощность объединения конечных множеств через мощности и мощности всех их возможных пересечений.
Для случая из двух множеств формула включения-исключения имеет следующий вид:
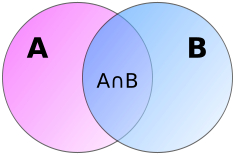
В силу того, что в сумме элементы пересечения учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера—Венна для двух множеств, приведенной на рисунке справа.
Для случая с большим количеством рассматриваемых множеств процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.
Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств.
| Теорема: |
Пусть , тогда по формуле включения—исключения: |
| Доказательство: |
|
Приведем два разноплановых доказательства теоремы. I. Комбинаторное доказательство теоремы. Рассмотрим некоторый элемент . Пусть . Тогда найдем число вхождений элемента в правую часть формулы.
Докажем, что В силу того, что , имеем , то равенство доказано. Таким образом, , то есть каждый элемент подсчитан в правой части формулы ровно один раз, то теорема доказана. II. Доказательство теоремы по индукции. Пусть — это количество множеств, мощность пересечения которых мы ищем. Для случая равенство обращается в тривиальное ( — истинно). Для случая справедливость теоремы пояснена выше. Таким образом, — база индукции. Предположим, что для равенство верно. Докажем, что равенство истинно для
Равенство справедливо, потому что все наборы можно разбить на две группы :
Как видно из равенства, первое и третье слагаемое "отвечают" за вторую группу, а второе слагаемое за первую группу. Значит, равенство истинно и . Таким образом, для мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана. |
Беспорядки
Беспорядком в комбинаторике называется перестановка чисел от до , в которой ни один элемент не стоит на своём месте.
| Теорема: |
Количество всех беспорядков порядка или субфакториалом числа (обозначение: !) может быть вычислено по формуле: |
Доказательство:
Воспользуемся принципом включения-исключения: обозначим за ![]() — количество перестановок из элементов, в каждой из которых -ый элемент стоит на своём месте. Тогда по формуле включения-исключения имеем:
— количество перестановок из элементов, в каждой из которых -ый элемент стоит на своём месте. Тогда по формуле включения-исключения имеем:
ИЛИ
Данные формулы являются эквивалентными. Действительно, если некоторое множество являются подмножествами некоторого множества ![]() , то, в силу законов де Моргана
, то, в силу законов де Моргана
В данной задаче множество ![]() — есть количество перестановок из элементов, т.е. . Верхнее подчеркивание или символ перед означает дополняющее множество до
— есть количество перестановок из элементов, т.е. . Верхнее подчеркивание или символ перед означает дополняющее множество до ![]()
![]() — количество перестановок, где -ый элемент стоит НЕ на своём -ом месте.
— количество перестановок, где -ый элемент стоит НЕ на своём -ом месте.
Таким образом величина в левой части формулы 2) — есть количество перестановок, где на 1-ой позици НЕ 1, на 2-ой позици НЕ 2 и т.д. То есть количество искомых беспорядков. Осталось определить величины в правой части:
|![]() | — количество перестановок с уже занятой позицией |
| — количество перестановок с уже занятой позицией |![]() | . Суммирование ведется по всем
| . Суммирование ведется по всем ![]()
Производя аналогичные рассуждения, получаем, что сумма пересечений некоторых множеств (то есть сумма всеx перестановки при некоторых зафиксированных позициях) — есть . Количество способов выбрать позиций — Количество перестановок с неподвижными точками:
Раскрывая по общеизвестной формуле, получим требуемое выражение, то есть количество беспорядков порядка .