Алгоритм Бойера-Мура — различия между версиями
Kabanov (обсуждение | вклад) |
Kabanov (обсуждение | вклад) |
||
| Строка 21: | Строка 21: | ||
Предположим, что в процессе сравнения возникает несовпадение между символом <tex>x[i]=a</tex> шаблона и символом <tex>y[i+j]=b</tex> исходного текста при проверке в позиции <tex>j</tex>. Тогда <tex>x[i+1 .. m-1]=y[i+j+1 .. j+m-1]=u</tex> и <tex>x[i] \neq y[i+j]</tex>, т.е. <tex>m - i - 1</tex> символов паттерна уже совпало. | Предположим, что в процессе сравнения возникает несовпадение между символом <tex>x[i]=a</tex> шаблона и символом <tex>y[i+j]=b</tex> исходного текста при проверке в позиции <tex>j</tex>. Тогда <tex>x[i+1 .. m-1]=y[i+j+1 .. j+m-1]=u</tex> и <tex>x[i] \neq y[i+j]</tex>, т.е. <tex>m - i - 1</tex> символов паттерна уже совпало. | ||
| + | |||
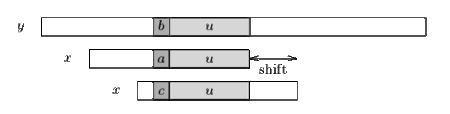
| + | Операция '''сдвига хорошего суффикса''' состоит в выравнивании подстроки <tex>u</tex> с его самым правым вхождением в <tex>x</tex>, что идет впереди символа, отличного от <tex>x[i]</tex>. | ||
[[Файл:boyer-moore-algorithm-1.gif|450px|center|The good-suffix shift, u re-occurs preceded by a character c different from a.]] | [[Файл:boyer-moore-algorithm-1.gif|450px|center|The good-suffix shift, u re-occurs preceded by a character c different from a.]] | ||
| + | |||
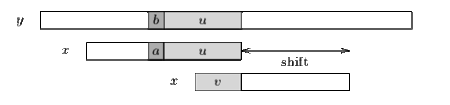
| + | Если не существует такого сегмента, то смещение состоит в выравнивании самого длинного суффикса <tex>v</tex> подстроки <tex>y[i+j+1 .. j+m-1]</tex> с соответствующим префиксом <tex>x</tex>. | ||
| + | |||
| + | [[Файл:boyer-moore-algorithm-2.gif|450px|center|The good-suffix shift, only a suffix of u re-occurs in x.]] | ||
| + | |||
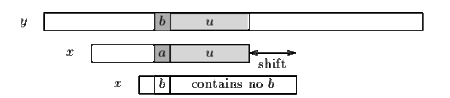
| + | Операция '''сдвига плохого символа''' состоит в выравнивании символа исходного текста <tex>у[i + j]</tex> с его самым правого появлением в <tex>x[0 .. m-2]</tex>. | ||
| + | |||
| + | [[Файл:boyer-moore-algorithm-3.gif|450px|center|The bad-character shift, a occurs in x.]] | ||
==Псевдо-код== | ==Псевдо-код== | ||
Версия 17:36, 9 мая 2014
Алгоритм Бойера-Мура, разработанный двумя учеными – Бойером (Robert S. Boyer) и Муром (J. Strother Moore), считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска подстроки в строке. Важной особенностью алгоритма является то, что он выполняет сравнения справа налево в отличии от многих других алгоритмов.
Алгоритм Бойера-Мура считается наиболее эффективным алгоритмом поиска шаблонов в стандартных приложениях и командах, таких как Ctrl+F в браузерах и текстовых редакторах.
Содержание
Асимптотики
Фаза предварительных вычислений требует времени и памяти В худшем случае поиск требует сравнений. В лучшем случае требует сравнений.
В 1991 году Р.Коул доказал следующую теорему:
| Теорема (Richard Cole): |
В худшем случае требуется сравнений в случае шаблона с периодом равным длине самого шаблона. |
| Доказательство: |
| Доказательство [1] |
Алгоритм
Алгоритм сравнивает символы шаблона () справа налево, начиная с самого правого, один за другим с символами исходной строки (). В случае несовпадения какого-либо символа (или полного совпадения всего шаблона) он использует две предварительно вычисляемых функций, чтобы сдвинуть позицию для начала сравнения вправо.
Пусть и .
Предположим, что в процессе сравнения возникает несовпадение между символом шаблона и символом исходного текста при проверке в позиции . Тогда и , т.е. символов паттерна уже совпало.
Операция сдвига хорошего суффикса состоит в выравнивании подстроки с его самым правым вхождением в , что идет впереди символа, отличного от .
Если не существует такого сегмента, то смещение состоит в выравнивании самого длинного суффикса подстроки с соответствующим префиксом .
Операция сдвига плохого символа состоит в выравнивании символа исходного текста с его самым правого появлением в .
Псевдо-код
void preBmBc(char *x, int m, int bmBc[]) {
int i;
for (i = 0; i < ASIZE; ++i)
bmBc[i] = m;
for (i = 0; i < m - 1; ++i)
bmBc[x[i]] = m - i - 1;
}
void suffixes(char *x, int m, int *suff) {
int f, g, i;
suff[m - 1] = m;
g = m - 1;
for (i = m - 2; i >= 0; --i) {
if (i > g && suff[i + m - 1 - f] < i - g)
suff[i] = suff[i + m - 1 - f];
else {
if (i < g)
g = i;
f = i;
while (g >= 0 && x[g] == x[g + m - 1 - f])
--g;
suff[i] = f - g;
}
}
}
void preBmGs(char *x, int m, int bmGs[]) {
int i, j, suff[XSIZE];
suffixes(x, m, suff);
for (i = 0; i < m; ++i)
bmGs[i] = m;
j = 0;
for (i = m - 1; i >= 0; --i)
if (suff[i] == i + 1)
for (; j < m - 1 - i; ++j)
if (bmGs[j] == m)
bmGs[j] = m - 1 - i;
for (i = 0; i <= m - 2; ++i)
bmGs[m - 1 - suff[i]] = m - 1 - i;
}
void BM(char *x, int m, char *y, int n) {
int i, j, bmGs[XSIZE], bmBc[ASIZE];
/* Preprocessing */
preBmGs(x, m, bmGs);
preBmBc(x, m, bmBc);
/* Searching */
j = 0;
while (j <= n - m) {
for (i = m - 1; i >= 0 && x[i] == y[i + j]; --i);
if (i < 0) {
OUTPUT(j);
j += bmGs[0];
}
else
j += MAX(bmGs[i], bmBc[y[i + j]] - m + 1 + i);
}
}