Контактная схема

Для математического описания электротехнических устройств, состоящих из контактов и промежуточных реле, функционирующих в дискретные моменты времени применяются контактные схемы.

Определение:

Контактная схема (англ. contact sheme) представляет собой ориентированный ациклический граф, на каждом ребре которого написана переменная или ее отрицание.

Определение:

Контакт (англ. contact) ребро схемы, помеченное символом переменной или ее отрицанием

Принцип работы

Пусть [math]u[/math] и [math]v[/math] — 2 полюса контактной схемы [math]S[/math], [math][u,v][/math] — некоторая цепь, соединяющая [math]u[/math] и [math]v[/math], [math]K(u,v)[/math] — конъюнкция букв прописанных на ребрах [math][u,v][/math]. Пусть функция [math]f(x^n)[/math] определяется формулой: [math]f(x^n)={\bigvee\limits_{[u,v]} (K(u,v))}[/math] в которой дизъюнкция берется по всем простым цепям схемы, соединяющие полюса [math]u[/math] и [math]v[/math]. Говорят, что схема [math]S[/math] реализует функцию [math]g(x^n)[/math], если [math]f(x^n)=g(x^n)[/math].

Построение контактных схем

Представление одного из базисов в контактных схемах

Любую булеву функцию можно представить в виде контактной схемы. Для этого необходимо привести её к ДНФ или КНФ, а затем построить, используя комбинации 3 логических элементов:

Конъюнкция

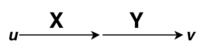
Результат конъюнкции равен [math]1[/math] тогда и только тогда, когда оба операнда равны [math]1[/math]. В применении к контактным схемам это означает, что последовательное соединение полюсов соответствует операции конъюнкции.

Дизъюнкция

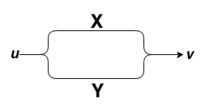
Результат дизъюнкции равен [math]0[/math] только в случае, когда оба операнда равны [math]0[/math]. Несложно догадаться, что в контактных схемах эта операция соответствует параллельному соединению полюсов.

Отрицание

Отрицание — это унарная операция, поэтому, чтобы показать её на контактной схеме достаточно написать над контактом знак отрицания.

Примеры построения некоторых функций

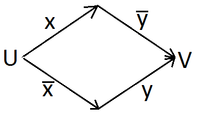
Исключающее "или"

[math]x \oplus y = (\neg x \land y) \lor (x \land \neg y)[/math]

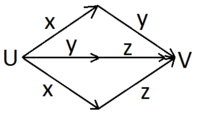
Медиана трех

[math] \langle x,y,z \rangle = (x \land y) \lor (x \land z) \lor (y \land z) \lor (x \land y \land z) = (x \land y) \lor (x \land z) \lor (y \land z)[/math]

Задача о минимизации контактной схемы

Определение:

Две контактные схемы называются эквивалентными, если они реализуют одну и ту же булеву функцию.

Определение:

Сложностью контактной схемы — число ее контактов.

Определение:

Минимальная контактная схема — схема, имеющая наименьшую сложность среди эквивалентных ей схем.

Задача минимизации контактных схем состоит в том, чтобы по данной схеме [math]S[/math] найти схему [math]T[/math] , эквивалентную [math]S[/math] и имеющую наименьшую сложность. Один из путей решения этой задачи состоит в следующем:

• Осуществляем переход от контактной схемы [math]S[/math] к её булевой функции [math]F(S)[/math].
• Упрощаем [math]F(S)[/math], то есть отыскиваем функцию [math]G[/math] (на том же базисе, что и [math]F(S)[/math], равносильную [math]F(S)[/math] и содержащую меньше вхождений операций дизъюнкции и конъюнкции. Для этой операции удобно использовать карты Карно.
• Строим схему [math]T[/math], реализующую функцию [math]G[/math].

Теорема:

Любой булеву функцию можно представить контактной схемой, сложностью [math]O(2^n)[/math]

Доказательство:

[math]\triangleright[/math]

Построим дерево конъюнктов для n переменных и их отрицаний. Это дерево будет содержать [math]O(2^n)[/math] контактов. Внизу дерева получится [math]2^n[/math] вершин. Очевидно, что каждая вершина соответствует одному конъюнкту. Если соединить часть из этих вершин с вершиной [math]v[/math] ребрами, на которых написана [math]1[/math], то сложность полученной схемы не изменится. Поэтому любую булевую функцию можно представить контактной схемой, сложностью [math]O(2^n)[/math]

[math]\triangleleft[/math]

См также

Построение функциональной схемы

Ссылки

• Контактные схемы
• Encyclopedia of Math — Contact sheme
• Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике