Квантовые гейты — различия между версиями
(→Применение квантовых гейтов) |
|||
| Строка 133: | Строка 133: | ||
* Разложить число на множители за <tex>n^2</tex>. Постановка задачи разложения числа на множители выглядит следующим образом: на вход подается составное число <tex>N</tex> в двоичной записи, на выход должны быть выданы два числа <tex>p, q,</tex> такие что <tex>N = pq</tex>. Типичный размер <tex>N</tex> порядка <tex>2^{2000}</tex>. Мотивацией для решения данной задачи является отсутствие на данный момент полиномиального классического алгоритма. Решение этой задачи позволит, например, взломать систему RSA. Лучший из известных классических алгоритмов имеет <tex>O(2^{\sqrt[3]{n}})</tex> в качестве оценки времени работы. Уже сегодня существует квантовый алгоритм, который решает эту задачу за <tex>O(n^2)</tex> [Питер Шор, 1994]. | * Разложить число на множители за <tex>n^2</tex>. Постановка задачи разложения числа на множители выглядит следующим образом: на вход подается составное число <tex>N</tex> в двоичной записи, на выход должны быть выданы два числа <tex>p, q,</tex> такие что <tex>N = pq</tex>. Типичный размер <tex>N</tex> порядка <tex>2^{2000}</tex>. Мотивацией для решения данной задачи является отсутствие на данный момент полиномиального классического алгоритма. Решение этой задачи позволит, например, взломать систему RSA. Лучший из известных классических алгоритмов имеет <tex>O(2^{\sqrt[3]{n}})</tex> в качестве оценки времени работы. Уже сегодня существует квантовый алгоритм, который решает эту задачу за <tex>O(n^2)</tex> [Питер Шор, 1994]. | ||
* Сделать полный перебор за <tex>{\sqrt{n}}</tex> <ref>[https://ru.wikipedia.org/wiki/%C0%EB%E3%EE%F0%E8%F2%EC_%C3%F0%EE%E2%E5%F0%E0 Алгоритм Гровера]</ref> | * Сделать полный перебор за <tex>{\sqrt{n}}</tex> <ref>[https://ru.wikipedia.org/wiki/%C0%EB%E3%EE%F0%E8%F2%EC_%C3%F0%EE%E2%E5%F0%E0 Алгоритм Гровера]</ref> | ||
| − | * Осуществить дискретный алгоритм нахождения логарифма за полиномиальное время | + | * Осуществить дискретный алгоритм нахождения логарифма за полиномиальное время<ref>[https://ru.wikipedia.org/wiki/%C4%E8%F1%EA%F0%E5%F2%ED%EE%E5_%EB%EE%E3%E0%F0%E8%F4%EC%E8%F0%EE%E2%E0%ED%E8%E5 Дискретное логарифмирование]</ref> |
* Создать стойкую криптосистему: если "подслушать" квантовый бит, то он изменится <ref>[http://habrahabr.ru/post/127461/ Квантовая криптография стучится в дверь]</ref> | * Создать стойкую криптосистему: если "подслушать" квантовый бит, то он изменится <ref>[http://habrahabr.ru/post/127461/ Квантовая криптография стучится в дверь]</ref> | ||
Построение квантового компьютера в виде реального физического прибора является фундаментальной задачей физики XXI века. В настоящее время построены только ограниченные его варианты (в пределах 512 кубит). | Построение квантового компьютера в виде реального физического прибора является фундаментальной задачей физики XXI века. В настоящее время построены только ограниченные его варианты (в пределах 512 кубит). | ||
Версия 17:01, 24 декабря 2014
Идея квантового компьютера, высказанная Фейнманом (англ. Richard Phillips Feynman) в 1982 году, достаточно проста. Она состоит в построении компьютера на основе квантовых, а не классических элементарных ячеек. Законы квантовой механики, определяющие поведение таких квантовых битов (англ. quantum bit) – кубитов, обеспечивают огромные преимущества (скорость и параллелизм вычислений) квантового компьютера по сравнению с классическим компьютером.
| Определение: |
| Любая логическая операция с кубитами называется квантовым гейтом (англ. quantum gate). |
По числу задействованных кубитов гейты делятся на одно- и многокубитные. Набор кубитов составляет квантовый регистр. Гейт переводит одно состояние регистра в другое.
Действие гейта на регистр можно записать так: .
Гейты – линейные операции: .
Содержание
Демонстрация действия гейта на кубит
Состояния квантовой системы и их преобразования можно описать используя компактные бра/кет обозначения, введённые Дираком. Кет-векторами обозначают вектор-столбцы и обычно используют для описания квантовых состояний. Парными бра-векторами обозначают сопряжение и транспонирование кет-векторов.
Для демонстрации действия гейта на кубиты используют матричную запись гейта или таблицу истинности.
Матрица гейта умножается на столбец весовых коэффициентов регистра и получается новый столбец, соответствующий новому состоянию регистра. В случае, если в действии гейта не участвуют некоторые кубиты, то их и не включают в матрицу, т.e. в матрице записано только реальное действие кубитов.
Таблица истинности отражает действие гейта на базисные состояния. Ее структура имеет следующий вид: по горизонтали записывается слева начальные состояния входящих кубитов, а справа — соответствующие конечные. По вертикали записываются все базисные состояния. Пример матричной записи кубита и таблиц истинности будет дан в таблице ниже.
Также используется графическая форма записи квантовых алгоритмов. Гейты обозначаются некоторыми символами (часто это кружок или квадрат с цифрой или буквой внутри). Кубиты представлены горизонтальными нитями. Действие гейта на кубит показывается путем "нанизывания" гейта на нужный кубит (или несколько кубитов, если это не однобитный гейт). Квантовый алгоритм представляется в виде сети таких гейтов и называется квантовой сетью. Слева в такой сети находятся начальные состояния кубитов, справа — конечные. Действие алгоритма заключается в прохождении кубитов по своим нитям через гейты слева направо.
Отличие кубитов от классических битов
Классический компьютер состоит из элементарных ячеек – битов, двум состояниям которых приписываются значения или . В наборе битов (регистре) записывается и обрабатывается информация в виде двоичных чисел. Один бит имеет два базисных состояния и . Система из битов имеет базисных состояний. Перебирая эти базисные состояния, можно закодировать двоичное число длиной . Например, в системе из трех битов можно записать одну из восьми последовательностей нулей и единиц .
В квантовом компьютере элементарными ячейками для записи информации являются квантовые биты – кубиты. Кубит – это квантовая система, которая, как и бит, имеет два базисных состояния и , но в отличие от бита, кубит может находиться в любом суперпозиционном состоянии . Состояние кубита – "немного" (с вероятностью ) ложно и "немного" (с вероятностью ) истинно.
Наиболее важным отличием кубитов от классических битов является не непрерывная природа суперпозиционных состояний, а возможность квантового перепутывания состояний в системе кубитов. В квантовой механике размерность пространства состояний системы в целом есть произведение (а не сумма) размерностей пространств состояний отдельных подсистем. Система из кубитов имеет , а не базисных состояний. Произвольное состояние N кубитов содержит все возможные бинарные строки (комбинации из нулей и единиц) длиной . В приведенном выше примере для все двоичных чисел могут быть закодированы в трех кубитах одновременно.
Описание используемых гейтов
В квантовом случае, как и в теории классических вычислений, любую обратимую унитарную операцию на кубитах можно представить как совокупность базовых операций. Базисом квантовой логики может служить один трехкубитный гейт (например Тоффоли или Фредкина ) или один однокубитный и один двукубитный гейт (например и )
Однокубитный гейт
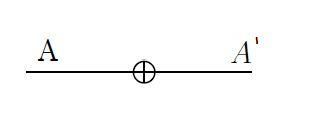
Однокубитная логическая операция переводит в .
т.e. переставляет весовые коэффициенты кубита местами. В классическом случае ей соответствует обычный , т.к. один из коэффициентов равен нулю.
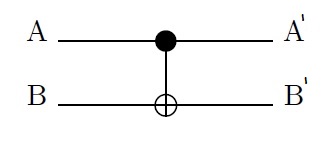
Двукубитный гейт
Двубитный гейт (Controlled NOT), действующий на двукубитное состояние в общем виде записывается так:
В классическом случае это просто .
Другие используемые гейты
Кроме упомянутых выше гейтов и в квантовых вычислениях используются также некоторые другие гейты. Их применение не необходимо, но запись алгоритма с их помощью намного проще. На практике часто используются такие гейты: однобитный (англ. Hadamard), двубитный (англ. swap), трехбитные (гейт Тоффоли), (гейт Фредкина).
Гейт Тоффоли инвертирует кубит при условии что значение кубитов и равны .
Гейт Фредкина устроен следующим образом: он осуществляет перестановку кубитов и при условии, что значение кубита равно .
Таблица различных обозначений квантовых гейтов
| название гейта | графическое обозначение | матричная запись | таблица истинности |
|---|---|---|---|
 |
|||
 |
|||
| (Hadamard) |  |
||
| (swap) | 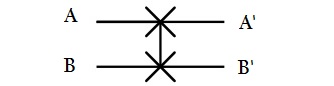 |
||
| (Toffoli) | 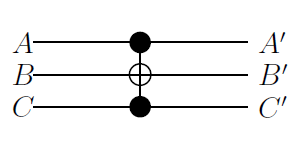 |
| |
| (гейт Фредкина) | 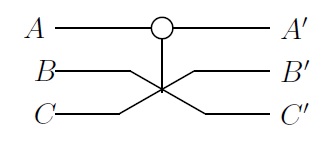 |
Применение квантовых гейтов
Квантовая модель вычислений позволяет:
- Разложить число на множители за . Постановка задачи разложения числа на множители выглядит следующим образом: на вход подается составное число в двоичной записи, на выход должны быть выданы два числа такие что . Типичный размер порядка . Мотивацией для решения данной задачи является отсутствие на данный момент полиномиального классического алгоритма. Решение этой задачи позволит, например, взломать систему RSA. Лучший из известных классических алгоритмов имеет в качестве оценки времени работы. Уже сегодня существует квантовый алгоритм, который решает эту задачу за [Питер Шор, 1994].
- Сделать полный перебор за [1]
- Осуществить дискретный алгоритм нахождения логарифма за полиномиальное время[2]
- Создать стойкую криптосистему: если "подслушать" квантовый бит, то он изменится [3]
Построение квантового компьютера в виде реального физического прибора является фундаментальной задачей физики XXI века. В настоящее время построены только ограниченные его варианты (в пределах 512 кубит).
В 2005 году группой Ю. Пашкина при помощи японских специалистов был построен двухкубитный квантовый процессор на сверхпроводящих элементах.
В ноябре 2009 года физикам из Национального института стандартов и технологий в США впервые удалось собрать программируемый квантовый компьютер, состоящий из двух кубит.
11 мая 2011 года представлен компьютер D-Wave One, созданный на базе 128-кубитного процессора.
В декабре 2012 года представлен новый процессор Vesuvius, который объединяет 512 кубит.