Символ Похгаммера — различия между версиями
| Строка 41: | Строка 41: | ||
Убывающий и растущий факториалы определены так же и в любом ассоциативном кольце с единицей и, следовательно, <tex dpi=150>x</tex> может быть даже комплексным числом, многочленом с комплексными коэффициентами или любой функцией определенной на комплексных числах. | Убывающий и растущий факториалы определены так же и в любом ассоциативном кольце с единицей и, следовательно, <tex dpi=150>x</tex> может быть даже комплексным числом, многочленом с комплексными коэффициентами или любой функцией определенной на комплексных числах. | ||
| − | + | ===Связывающие коэффициенты=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Так как убывающие факториалы {{---}} базис кольца многочленов, мы можем переписать произведение двух из них как линейную комбинацию убывающих факториалов: | Так как убывающие факториалы {{---}} базис кольца многочленов, мы можем переписать произведение двух из них как линейную комбинацию убывающих факториалов: | ||
| Строка 69: | Строка 64: | ||
:<tex dpi=150>x^{(n)} = {(-1)}^n {(-x)}_{{n}} .</tex> | :<tex dpi=150>x^{(n)} = {(-1)}^n {(-x)}_{{n}} .</tex> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Отношение двух символов Похгаммера определяется как: | Отношение двух символов Похгаммера определяется как: | ||
| Строка 86: | Строка 75: | ||
:<tex dpi=150>(x)_{-n} = \frac{1}{(x-n)_n} = \frac{1}{(x-1)^{\underline{n}}}</tex> | :<tex dpi=150>(x)_{-n} = \frac{1}{(x-n)_n} = \frac{1}{(x-1)^{\underline{n}}}</tex> | ||
:<tex dpi=150>x^{\underline{-n}} = \frac{1}{(x+1)_n} = \frac{1}{n! \binom{x+n}{n}} = \frac{1}{(x+1)(x+2) \cdots (x+n)}</tex> | :<tex dpi=150>x^{\underline{-n}} = \frac{1}{(x+1)_n} = \frac{1}{n! \binom{x+n}{n}} = \frac{1}{(x+1)(x+2) \cdots (x+n)}</tex> | ||
| + | |||
| + | ====Числа Стирлинга второго рода==== | ||
| + | Убывающий и растущий факториалы выражаются друг через друга при помощи [[Числа Стирлинга второго рода|чисел Стирлинга второго рода]]: | ||
| + | <ref name="Introduction to the factorials and binomials">[http://functions.wolfram.com/GammaBetaErf/Factorial/introductions/FactorialBinomials/05/ Wolfram Functions Site {{---}} Introduction to the factorials and binomials]</ref> | ||
| + | |||
| + | <tex dpi=150> x^n = \sum_{k=0}^{n} \left\{\begin{matrix} n \\ n-k \end{matrix} \right\} x^{\underline{n-k}} </tex> | ||
| + | :<tex dpi=150> = \sum_{k=0}^{n} \left\{\begin{matrix} n \\ k \end{matrix} \right\}(-1)^{n-k} (x)_k. </tex> | ||
| + | |||
| + | ====Числа Лаха==== | ||
| + | Убывающий и растущий факториалы связаны друг с другом [[wikipedia:Lah number|числами Лаха]]: | ||
| + | <ref name="Introduction to the factorials and binomials">[http://functions.wolfram.com/GammaBetaErf/Factorial/introductions/FactorialBinomials/05/ Wolfram Functions Site {{---}} Introduction to the factorials and binomials]</ref> | ||
| + | {{Утверждение | ||
| + | |id= | ||
| + | |author= | ||
| + | |about= | ||
| + | |statement=<tex dpi=150> x^{(n)} = \sum_{k=1}^n \binom{n-1}{k-1} \frac{n!}{k!} \times (x)_k </tex> | ||
| + | |proof= | ||
| + | Подставим целое <tex dpi=150>m</tex> из отрезка <tex dpi=150>[0;n]</tex>, тогда получим (будем считать, что <tex dpi=150>(-1)!</tex> равно бесконечности): | ||
| + | :<tex dpi=150>\frac{(n+m-1)!}{(m-1)!}=\sum_{k=1}^n \frac{(n-1)!}{(k-1)!(n-k)!}\times\frac{n!}{k!}\times\frac{m!}{(m-k)!}</tex> | ||
| + | Поделим обе части на <tex dpi=150>n!</tex>, а из правой части уберём слагаемые, равные нулю, {{---}} получим: | ||
| + | :<tex dpi=150>\binom{n+m-1}{n}=\sum_{k=1}^{min(m,k)} \binom{n-1}{n-k}\times\binom{m}{k}</tex> | ||
| + | Это тождество очевидно из комбинаторики, так как обе части равны числу способов выбрать из <tex dpi=150>n+m-1</tex> элементов, разделённых на два множества по <tex dpi=150>n-1</tex> и <tex dpi=150>m</tex> элементов, <tex dpi=150>n</tex> элементов. С одной стороны нельзя не признать, что это левая часть тождества по определению бинома. С другой стороны нельзя не согласиться, что это правая часть тождества, в котором <tex dpi=150>k</tex> означает количество элементов, берущихся из множества размера <tex dpi=150>m</tex>. | ||
| + | Многочлены, стоящие в левой и правой частях тождества, оказались равны в <tex dpi=150>n+1</tex> точке и при этом имеют степень не больше <tex dpi=150>n</tex>, то есть они формально совпадают, что и требовалось доказать. | ||
| + | }} | ||
===Гамма функция=== | ===Гамма функция=== | ||
| Строка 135: | Строка 148: | ||
:<tex dpi=150>D^n(x^a) = (a)_n\,\, x^{a-n}.</tex> | :<tex dpi=150>D^n(x^a) = (a)_n\,\, x^{a-n}.</tex> | ||
| + | |||
| + | ===Теорема об умножении=== | ||
| + | По [[wikipedia:Multiplication theorem|теореме об умножении]] получаем следующие выражения для растущего факториала: | ||
| + | |||
| + | :<tex dpi=150>(x)_{k+mn} = (x)_k m^{mn} \prod_{j=0}^{m-1} \left(\frac{x+j+k}{m}\right)_n,\ m \in \mathbb{N} </tex> | ||
| + | :<tex dpi=150>(ax+b)_n = x^n \prod_{k=0}^{x-1} \left(a+\frac{b+k}{x}\right)_{n/x},\ x \in \mathbb{Z}^{+} </tex> | ||
| + | :<tex dpi=150>(2x)_{2n} = 2^{2n} (x)_n \left(x+\frac{1}{2}\right)_n. </tex> | ||
==Обобщения== | ==Обобщения== | ||
Версия 19:13, 19 января 2018
| Определение: |
| В математике убывающим факториалом (англ. falling factorial) (иногда называется нисходящим факториалом, постепенно убывающим факториалом или нижним факториалом) обозначают:
|
| Определение: |
| Растущий факториал (англ. rising factorial) (иногда называется функцией Похгаммера, многочленом Похгаммера, восходящим факториалом, постепенно растущим произведением или верхним факториалом) определяется следующей формулой:
|
Грахам, Кнут и Паташник[1] предложили произносить эти записи как " растущий к " и " убывающий к " соответственно.
При значение принимается равным (пустое произведение).
В зависимости от контекста символ Похгаммера может обозначать как растущий факториал, так и убывающий факториал. Сам Лео Август Похгаммер для себя использовал в другом смысле - для обозначения биномиального коэффициента .
Когда неотрицательное целое число, равняется числу инъективных отображений из множества с элементами во множество из элементов. Для обозначения этого числа часто применяют обозначения и . Символ Похгаммера в основном используется в алгебре, где — переменная, то есть есть ни что иное как многочлен степени от .
Другие формы записи убывающего факториала: , , , или .
Другое обозначение растущего факториала реже встречается, чем . Обозначение используется для растущего факториала, запись обычно применяется для обозначения убывающего факториала для избежания недоразумений.[2]
Содержание
Примеры
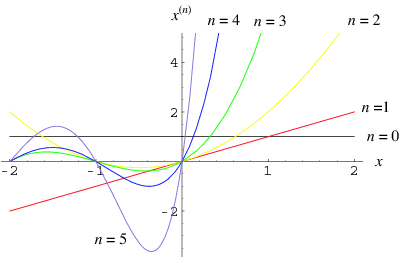
Несколько первых растущих факториалов:
Несколько первых убывающих факториалов:
Коэффициенты в выражениях являются числами Стирлинга первого рода.
Свойства
Убывающий и растущий факториалы определены так же и в любом ассоциативном кольце с единицей и, следовательно, может быть даже комплексным числом, многочленом с комплексными коэффициентами или любой функцией определенной на комплексных числах.
Связывающие коэффициенты
Так как убывающие факториалы — базис кольца многочленов, мы можем переписать произведение двух из них как линейную комбинацию убывающих факториалов:
| Определение: |
| Коэффициенты называются связывающими коэффициентами (англ. connection coefficients). Связывающие коэффициенты имеют комбинаторную интерпретацию как число способов объединить элементов из множеств размера и . |
Биномиальный коэффициент
Растущий и убывающий факториалы могут быть использованы для обозначения биномиального коэффициента:
Таким образом, многие свойства биномиальных коэффициентов справедливы для убывающих и растущих факториалов.
Связь убывающего и растущего факториалов
Растущий факториал может быть выражен как убывающий факториал, начинающийся с другого конца,
или как убывающий с противоположным аргументом,
Отношение двух символов Похгаммера определяется как:
Кроме того, мы можем развернуть экспоненты и убывающие факториалы как:
Числа Стирлинга второго рода
Убывающий и растущий факториалы выражаются друг через друга при помощи чисел Стирлинга второго рода: [3]
Числа Лаха
Убывающий и растущий факториалы связаны друг с другом числами Лаха: [3]
| Утверждение: |
|
Подставим целое из отрезка , тогда получим (будем считать, что равно бесконечности): Поделим обе части на , а из правой части уберём слагаемые, равные нулю, — получим: Это тождество очевидно из комбинаторики, так как обе части равны числу способов выбрать из элементов, разделённых на два множества по и элементов, элементов. С одной стороны нельзя не признать, что это левая часть тождества по определению бинома. С другой стороны нельзя не согласиться, что это правая часть тождества, в котором означает количество элементов, берущихся из множества размера . Многочлены, стоящие в левой и правой частях тождества, оказались равны в точке и при этом имеют степень не больше , то есть они формально совпадают, что и требовалось доказать. |
Гамма функция
Растущий факториал может быть продолжен на вещественные значения , но с использованием Гамма функции при условии, что и вещественные числа, но не отрицательные целые.
| Утверждение: |
|
— по определению. Значит,
Объединив эти два факта, получим, что:
|
то же самое и про убывающий факториал:
| Утверждение: |
|
— по определению. Значит,
Объединив эти два факта, получим, что:
|
Дифференциал
Если означает производную по , то
Теорема об умножении
По теореме об умножении получаем следующие выражения для растущего факториала:
Обобщения
Обобщенный символ Похгаммера называется обобщённый символ Похгаммера, используемый в многомерном математическом анализе. Также существует q-аналог — q-Похгаммер символ.
Обобщение убывающего факториала, в которой функция вычисляется по нисходящей арифметической последовательности целых чисел, а значения перемножаются как:
где декремент и число факторов. Соответствующее обобщения растущего факториала:
Эта запись объединяет растущий и убывающий факториалы, которые и соответственно.
Для арифметической функции и параметров определен обобщенное факториальное произведение вида:
См.также
- Гамма функция
- Числа Стирлинга первого рода
- Числа Стирлинга второго рода
- Инъективное отображение
- Обобщённый символ Похгаммера
- q-Похгаммер символ
- Числа Лаха
- Теорема об умножении
- q-аналог
Примeчания
- ↑ Ronald L. Graham, Donald E. Knuth and Oren Patashnik in their book Concrete Mathematics (), Addison-Wesley, Reading MA. ISBN , pp. ,
- ↑ According to Knuth, The Art of Computer Programming, Vol. , rd ed., p. .
- ↑ 3,0 3,1 Wolfram Functions Site — Introduction to the factorials and binomials