| Определение: |
В математике убывающим факториалом (англ. falling factorial) (иногда называется нисходящим факториалом, постепенно убывающим факториалом или нижним факториалом) обозначают:
- [math](x)_{n}=x^{\underline{n}}=x(x-1)(x-2)\cdots(x-n+1)=\prod\limits_{k=1}^{n}(x-(k-1))=\prod\limits_{k=0}^{n-1}(x-k)[/math]
При [math]n=0[/math] значение принимается равным [math]1[/math] (пустое произведение). |
| Определение: |
Растущий факториал (англ. rising factorial) (иногда называется функцией Похгаммера, многочленом Похгаммера, восходящим факториалом, постепенно растущим произведением или верхним факториалом) определяется следующей формулой:
- [math]x^{(n)}=x^{\overline{n}}=x(x+1)(x+2)\cdots(x+n-1)=\prod\limits_{k=1}^{n}(x+(k-1))=\prod\limits_{k=0}^{n-1}(x+k). [/math]
При [math]n=0[/math] значение принимается равным [math]1[/math] (пустое произведение). |
Грахам, Кнут и Паташник[1] предложили произносить эти записи как "[math]x[/math] растущий к [math]m[/math]" и "[math]x[/math] убывающий к [math]m[/math]" соответственно.
В зависимости от контекста символ Похгаммера может обозначать как растущий факториал, так и убывающий факториал.
Когда [math]x[/math] неотрицательное целое число, [math](x)_n[/math] равняется числу инъективных отображений[2] из множества с [math]n[/math] элементами во множество из [math]x[/math] элементов. Для обозначения этого числа часто применяют обозначения [math]_x P_n[/math] и [math]P(x,n)[/math]. Символ Похгаммера в основном используется в алгебре, где [math]x[/math] — переменная, то есть [math](x)_n[/math] есть ни что иное как многочлен степени [math]n[/math] от [math]x[/math].
Замечание
Другие формы записи убывающего факториала: [math]P(x,n)[/math], [math]^x P_n[/math], ,[math]P_{x,n}[/math] или [math]_x P_n[/math].
Другое обозначение растущего факториала [math]x^{(n)}[/math] реже встречается, чем [math](x)^+_n[/math]. Обозначение [math](x)^+_n[/math] используется для растущего факториала, запись [math](x)^-_n[/math] обычно применяется для обозначения убывающего факториала для избежания недоразумений.[3]
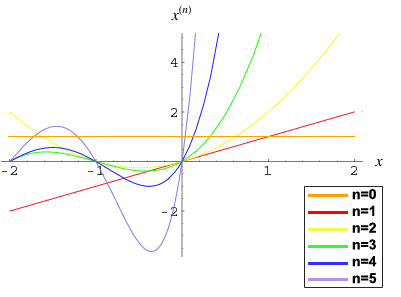
График растущего факториала для
[math]n[/math] от
[math]0[/math] до
[math]4[/math]Примеры
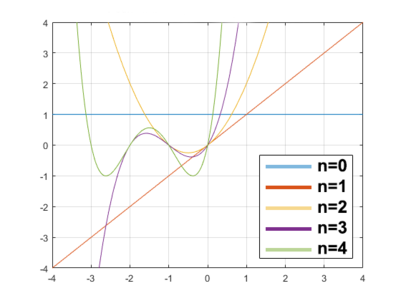
График убывающего факториала для
[math]n[/math] от
[math]0[/math] до
[math]4[/math]Несколько первых растущих факториалов:
- [math]x^{(0)}=x^{\overline0}=1 [/math]
- [math]x^{(1)}=x^{\overline1}=x [/math]
- [math]x^{(2)}=x^{\overline2}=x(x+1)=x^2+x [/math]
- [math]x^{(3)}=x^{\overline3}=x(x+1)(x+2)=x^3+3x^2+2x [/math]
- [math]x^{(4)}=x^{\overline4}=x(x+1)(x+2)(x+3)=x^4+6x^3+11x^2+6x [/math]
Несколько первых убывающих факториалов:
- [math](x)_{0}=x^{\underline0}=1 [/math]
- [math](x)_{1}=x^{\underline1}=x [/math]
- [math](x)_{2}=x^{\underline2}=x(x-1)=x^2-x [/math]
- [math](x)_{3}=x^{\underline3}=x(x-1)(x-2)=x^3-3x^2+2x [/math]
- [math](x)_{4}=x^{\underline4}=x(x-1)(x-2)(x-3)=x^4-6x^3+11x^2-6x [/math]
Коэффициенты в выражениях являются числами Стирлинга первого рода.
Свойства
Убывающий и растущий факториалы определены так же и в любом ассоциативном кольце с единицей и, следовательно, [math]x[/math] может быть даже комплексным числом, многочленом с комплексными коэффициентами или любой функцией определенной на комплексных числах.
Коэффициенты связи
Так как убывающие факториалы — базис кольца многочленов, мы можем переписать произведение двух из них как линейную комбинацию убывающих факториалов:
- [math](x)_m (x)_n = \sum\limits_{k=0}^m {m \choose k} {n \choose k} k!\, (x)_{m+n-k}.[/math]
| Определение: |
| Коэффициенты [math]{m \choose k} {n \choose k} k![/math], стоящие при [math](x)_{m+n-k}[/math], называются коэффициентами связи (англ. connection coefficients). |
Биномиальный коэффициент
Растущий и убывающий факториалы могут быть использованы для обозначения биномиального коэффициента:
- [math]\frac{x^{(n)}}{n!} = {x+n-1 \choose n} [/math] и [math]\frac{(x)_n}{n!} = {x \choose n}.[/math]
Таким образом, многие свойства биномиальных коэффициентов справедливы для убывающих и растущих факториалов.
Связь убывающего и растущего факториалов
Растущий факториал может быть выражен как убывающий факториал, начинающийся с другого конца,
- [math]x^{(n)} = {(x + n - 1)}_n [/math]
или как убывающий с противоположным аргументом,
- [math]x^{(n)} = {(-1)}^n {(-x)}_{{n}} [/math]
Отношение двух символов Похгаммера можно выразить следующим образом:
- [math]\frac{(x)_n}{(x)_i} = (x-i)_{n-i},\ n \geqslant i. [/math]
Убывающий факториал возможно выразить следующим способом:
- [math](x)_{m+n} = x_{m} (x-m)_{n}[/math]
- [math](x)_{-n} = \frac{1}{(x+1)(x+2) \cdots (x+n)} = \frac{1}{(x+1)^n} = \frac{1}{(x+n)_n} = \frac{1}{n! \binom{x+n}{n}}[/math]
Числа Стирлинга первого рода
Растущий факториал выражается с помощью чисел Стирлинга первого рода:
- [math]x^{(n)} = \sum\limits_{k=1}^n s(n,k) x^k[/math]
Числа Стирлинга второго рода
Убывающий и растущий факториалы выражаются друг через друга при помощи чисел Стирлинга второго рода:
[math] x^{(n)} = \sum\limits_{k=0}^{n} \left\{\begin{matrix} n \\ n-k \end{matrix} \right\} (x)_{n-k} [/math]
- [math] = \sum\limits_{k=0}^{n} \left\{\begin{matrix} n \\ k \end{matrix} \right\}(-1)^{n-k} (x)_k [/math]
Числа Лаха
Убывающий и растущий факториалы связаны друг с другом числами Лаха[4]:
| Утверждение: |
[math] x^{(n)} = \sum\limits_{k=1}^n (L(n,k) \times (x)_k) = \sum\limits_{k=1}^n (\binom{n-1}{k-1} \frac{n!}{k!} \times (x)_k) [/math] |
| [math]\triangleright[/math] |
|
Второе равенство получается из определения чисел Лаха. Поэтому осталось доказать лишь то, что левая часть равняется правой:
- [math] x^{(n)} =\sum\limits_{k=1}^n (\binom{n-1}{k-1} \frac{n!}{k!} \times (x)_k) [/math]
Подставим целое [math]m[/math] из отрезка [math][0;n][/math], тогда получим:
- [math] m^{(n)} =\sum\limits_{k=1}^n (\binom{n-1}{k-1} \frac{n!}{k!} \times (m)_k) [/math]
Заметим, что [math](m)_k=0[/math] при [math]m+1 \leqslant k[/math], поэтому слагаемые из суммы в правой части, начиная с [math]k\geqslant m+1[/math], равны нулю, то есть:
- [math]\sum\limits_{k=1}^n (\binom{n-1}{k-1} \frac{n!}{k!} \times (m)_k)=\sum\limits_{k=1}^{min(m,n)} (\binom{n-1}{k-1} \frac{n!}{k!} \times (m)_k)[/math]
Поделим обе части на [math]n![/math] и получим, что левая часть равна:
- [math]\frac{(n+m-1)!}{(m-1)!n!}=\frac{(n+m-1)!}{((n+m-1)-n)!n!}=\binom{n+m-1}{n}[/math]
а правая часть будет равна:
[math]\sum\limits_{k=1}^{min(m,n)} (\frac{(n-1)!}{(k-1)!(n-k)!}\times\frac{1}{k!}\times\frac{m!}{(m-k)!})=\sum\limits_{k=1}^{min(m,n)} (\frac{(n-1)!}{(k-1)!(n-k)!}\times\frac{m!}{k!(m-k)!})[/math]
- [math]=\sum\limits_{k=1}^{min(m,n)} (\frac{(n-1)!}{(k-1)!((n-1)-(k-1))!}\times\frac{m!}{k!(m-k)!})=\sum\limits_{k=1}^{min(m,n)} (\binom{n-1}{k-1}\times\binom{m}{k})[/math]
То есть мы хотим теперь доказать тождество:
- [math]\binom{n+m-1}{n}=\sum\limits_{k=1}^{min(m,n)} (\binom{n-1}{n-k}\times\binom{m}{k})[/math]
Это тождество очевидно из комбинаторики, так как обе части равны числу способов выбрать из [math]n+m-1[/math] элементов, разделённых на два множества по [math]n-1[/math] и [math]m[/math] элементов, [math]n[/math] элементов. С одной стороны нельзя не признать, что это левая часть тождества по определению сочетания. С другой стороны нельзя не согласиться, что это правая часть тождества, в котором [math]k[/math] означает количество элементов, берущихся из множества размера [math]m[/math], а [math]n-k[/math] из второго множества размера [math]n-1[/math].
Многочлены, стоящие в левой и правой частях тождества, оказались равны в [math]n+1[/math] точке и при этом имеют степень не больше [math]n[/math], то есть они формально совпадают. |
| [math]\triangleleft[/math] |
Гамма функция
Растущий факториал может быть продолжен на вещественные значения [math]n[/math], но с использованием Гамма функции[5] при условии, что [math]x[/math] и [math]x+n[/math] вещественные числа, но не отрицательные целые.
| Утверждение: |
[math]x^{(n)}=\frac{\Gamma(x+n)}{\Gamma(x)}[/math] |
| [math]\triangleright[/math] |
- [math]\Gamma(z+1) = z\Gamma(z)[/math] — для комплексного [math]z[/math].
Значит, это тождество верно и для [math]z=x[/math], где [math]x[/math] — вещественное число. То есть:
- [math]\Gamma(x) = (x-1)\Gamma(x-1)[/math] — для вещественного [math]x[/math].
Заметим тогда, что:
[math]\Gamma(x+n) = ((x+n)-1)\cdot\Gamma((x+n)-1) = ((x+n)-1)(x+n-2)\cdot\Gamma((x+n)-2)[/math]
- [math]= \cdots = ((x+n)-1)((x+n)-2)\cdots((x+n)-n)\cdot\Gamma((x+n)-n)[/math]
- [math]= ((x+n)-1)((x+n)-2)\cdots x\cdot\Gamma(x)[/math]
Значит:
[math]\frac{\Gamma(x+n)}{\Gamma(x)} = \frac{((x+n)-1)((x+n)-2)\cdots x\cdot\Gamma(x)}{\Gamma(x)}[/math]
- [math]= (x+n-1)(x+n-2)\cdots x = x(x+1)\cdots(x+n-1)=x^{(n)}[/math]
|
| [math]\triangleleft[/math] |
то же самое и про убывающий факториал:
| Утверждение: |
[math](x)_n=\frac{\Gamma(x+1)}{\Gamma(x-n+1)}[/math] |
| [math]\triangleright[/math] |
- [math]\Gamma(z+1) = z\Gamma(z)[/math] — для комплексного [math]z[/math].
Значит, это тождество верно и для [math]z=x[/math], где [math]x[/math] — вещественное число. То есть:
- [math]\Gamma(x+1) = x\Gamma(x)[/math] — для вещественного [math]x[/math].
Заметим тогда, что:
[math]\Gamma(x+1) = x\cdot\Gamma(x) = x(x-1)\cdot\Gamma(x-1)[/math]
- [math]= \cdots = x(x-1)\cdots(x-n+1)\cdot\Gamma(x-n+1)[/math]
Значит:
[math]\frac{\Gamma(x+1)}{\Gamma(x-n+1)} = \frac{x(x-1)\cdots(x-n+1)\cdot\Gamma(x-n+1)}{\Gamma(x-n+1)}[/math]
- [math]= x(x-1)\cdots(x-n+1) = (x)_n[/math]
|
| [math]\triangleleft[/math] |
Дифференциал
| Утверждение: |
[math]\frac{\partial^n(x^a)}{\partial x^n} = (a)_n\,\, x^{a-n}[/math] |
| [math]\triangleright[/math] |
|
[math]\frac{\partial^n(x^a)}{\partial x^n} =a\times\frac{\partial^{n-1}(x^{a-1})}{\partial x^{n-1}}=a(a-1)\times\frac{\partial^{n-2}(x^{a-2})}{\partial x^{n-2}}[/math]
- [math]=a(a-1)\cdots (a-n+2)\times\frac{\partial(x^{a-(n-1)})}{\partial x}=(a)_n\,\, x^{a-n}[/math]
|
| [math]\triangleleft[/math] |
Обобщения
Существует обобщённый символ Похгаммера[6], используемый в многомерном математическом анализе. Также существует [math]q[/math]-аналог[7] — [math]q[/math]-Похгаммер символ[8].
Обобщение убывающего факториала — функция, определённая следующим образом:
- [math][f(x)]^{k/-h}=f(x)\cdot f(x-h)\cdot f(x-2h)\cdots f(x-(k-1)h),[/math]
где [math]-h[/math] и [math]k[/math] — разница в убывающей арифметической прогрессии аргументов множителей и число множителей соответственно. Аналогичное обобщение растущего факториала:
- [math][f(x)]^{k/h}=f(x)\cdot f(x+h)\cdot f(x+2h)\cdots f(x+(k-1)h).[/math]
Эта запись объединяет растущий и убывающий факториалы, которые [math][x^{k/1}][/math] и [math][x^{k/-1}][/math] соответственно.
Для арифметической функции [math]f: \mathbb{N} \rightarrow \mathbb{C}[/math] и параметров [math]x, t[/math] определено обобщенное факториальное произведение вида:
- [math](x)_{n,f,t} = \prod\limits_{k=1}^{n-1} \left(x+\frac{f(k)}{t^k}\right)[/math]
См.также
Примeчания
Источники информации

