Список с пропусками

Пример списка с пропусками

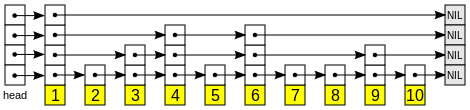
Список с пропусками (англ. skip list) — вероятностная структура данных, позволяющая в среднем за [math]O(\log(n))[/math] времени выполнять операции добавления, удаления и поиска элементов.

Список с пропусками состоит из нескольких уровней, на каждом из которых находится отсортированный связный список. На самом нижнем (первом) уровне располагаются все элементы. Дальше около половины элементов таким же образом располагаются на втором, почти четверть [math]-[/math] на третьем и так далее, но при этом известно, что если элемент расположен на каком-то уровне, то он также расположен на всех нижележащих уровнях.

Построение

Допустим, что нам задан односвязный отсортированный список и мы хотим построить на его основе список с пропусками, позволяющий в среднем за [math]O(\log{n})[/math] времени выполнять операции добавления, удаления и поиска элементов.

На самом нижнем уровне списка с пропусками мы расположим исходный список. На втором уровне [math]-[/math] всё элементы с чётными номерами, причём каждый элемент будет ссылаться на соответствующий ему элемент на нижнем уровне. Таким же образом построим и третий уровень, куда будем добавлять только те элемента, номера которых кратны четырём. Аналогично построим и последующие уровни.

Функция [math]\ \mathtt{build\_lvl} \ [/math] возвращает новый уровень списка с пропусками на основе предыдущего построенного уровня.

   list build_lvl (list lvl)                   // Отсеивание нечётных элементов
       list next_lvl 
       node i = lvl.head()                     // Перебор всех элементов lvl
       while (i != null) and (i != lvl.tail())
           next_lvl.push_back(node(i.key, i))  // Конструктор node(key, down) возвращает новую вершину с ключом key и ссылкой down на соответствующую вершину предыдущего уровеня
           i = i.next.next                     // Переход к следующему чётному элементу
       return next_lvl 

Функция [math]\ \mathtt{skip\_list} \ [/math] принимает в качестве аргумента односвязный отсортированный список и возвращает новый список с пропусками, построенный на его основе.

   list skip_list (list l):
       list lvl = build_lvl(l)                // Построение первого уровня
       while lvl.size() > 2                   // Добавление следующих уровней; последний содержит не более двух элементов
           lvl = build_lvl (lvl)                       
       return lvl                             // Возвращает ссылку на начало верхнего уровня

Операции над структурой

Поиск элемента

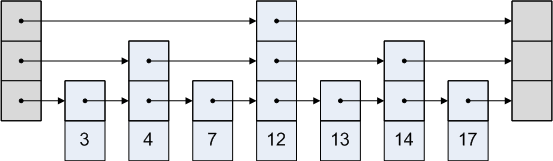
Допустим, что в нашем списке с пропусками существуют [math]k[/math] уровней, при этом первым уровнем будет исходный список.

В таком случае алгоритм поиска в этой структуре будет представлять из себя следующие операции:

1. Начинаем поиск элемента в верхнем списке
2. Переходим к следующему элементу списка, пока значение в следующей ячейке меньше или равно ключу
3. Переместиться на один уровень вниз и перейти к шагу [math]2[/math]. Если мы уже были на первом уровне [math]-[/math] прекратить поиск.

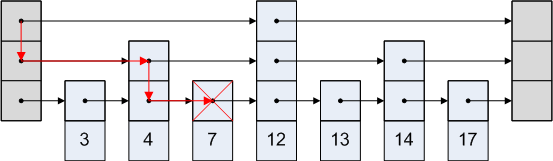
Пример поиска числа [math]8[/math] в списке из описания:

Если в качестве случайного источника мы будем использовать честную монету, то в среднем случае будет [math]\log{n}[/math] уровне. На самом верхнем уровне будет не более двух элементов. Тогда на каждом уровне в среднем нужно проверить не более двух элементов (в противном случае могли бы вместо двух нижних элементов проверить ещё один уровнем выше). Уровней всего [math]\log{n}[/math], откуда вытекает оценка времени поиска элемента в [math]O(\log{n})[/math].

Функция [math]\mathtt{find}[/math] возвращает ссылку на элемент, значение которого не меньше [math]\mathtt{key}[/math]. В случае, если все элементы в списке с пропусками меньше [math]\mathtt{key}[/math], то возвращается ссылка на конец списка с пропусками.

   T find (list skip_list, K key)
       node res 
       for (res = skip_list.head; res.ref != null; res = res.ref)     // Пока ещё не дошли до первого уровня 
           while res.key < key                                        // Пока значение вершины меньше ключа
               res = res.next()                                       // Перейти к следующей вершине в текущем уровне
       return res

Вставка элемента

Для вставки элемента в список с пропусками, нам необходимо выполнить следующие шаги:

1. Найти с помощью алгоритма поиска позицию, где мог бы находиться элемент.
2. Вставить наш элемент в текущий уровень списка с пропусками
3. Подбросить монету.
4. Если выпал «Орёл» то перейти на уровень выше и вернуться к шагу [math]2[/math]
5. Иначе закончить операцию вставки

Таким образом, если использовать честную монету, то математическое ожидание количества элементов на втором уровне равняется [math]\dfrac{n}{2}[/math], на третьем уровне [math]-[/math] [math]\dfrac{n}{4}[/math] и т.д. На уровне [math]\log{n}[/math] у нас окажется один элемент. Ну и соответственно вероятности попасть элементу на второй уровень — это [math]\dfrac{1}{2}[/math], на третий [math]\dfrac{1}{4}[/math] и т.д. Вероятность попасть на уровень [math]\log{n}[/math] равна [math]\dfrac{1}{n}[/math].

Используя монетку с распределением отличным от [math]\left\{\dfrac{1}{2}, \ \dfrac{1}{2}\right\}[/math], можно влиять на количество элементов на верхних уровнях. Так, например, при использовании монеты с распределением [math]\{p,q\}[/math] математическое ожидание количества элементов на уровне [math]k[/math] равно [math]n q^k[/math], на каждом следующем уровне будет в среднем в [math]q[/math] раз больше элементов. Таким образом, время поиска будет равно [math]O\left(\dfrac{k}{q} + nq^k\right)[/math]. Соответственно при честной монетке и [math]\log(n)[/math] уровней получаем оценку, полученную ранее. Для крайних распределений:

• [math]\{0, 1\}[/math] — [math]O(k+n)[/math]
• [math]\{1, 0\}[/math] — [math]\infty[/math] (если разрешить добавление новых уровней при проталкивании элемента после броска монетки; иначе [math]O(n)[/math])

   node insert (node i, K key, T data)
       while i.key <= key                   // Ищем подходящее место
           i = i.next() 
       node tmp = null                      // Для записи в поле down
       if i.ref != null                     // Мы не на нижнем уровне
           tmp = insert (i.ref, key)        // Рекурсивный вызов на более низком уровне
           if tmp == null                   // Проверка броска монетки
               return null 
       i.next = new node (i.next, tmp, data, key)  //Непосредственно вставка
       if random(0,1) > 0.5                 // Бросок монетки
           return i.next                    // Нужно передать новый элемент для вставки выше
       else
           return null 

   void insert (list skip_list, K key, T data) // Обёрточка
       insert(skip_list.head, key, data) 

Удаление элемента

Алгоритм удаления достаточно тривиален.

1. Найти удаляемый элемент
2. Удалить его со всех уровней

Функция [math]\mathtt{erase}[/math] удаляет вершину [math]i[/math] из списка с пропусками.

   void erase (node i, K key)
       if i == null
           return 
       while i.key <= key                   // Ищем элемент
           i = i.next() 
       erase(i.ref, key)                    // Удаляем с нижних уровней
       if i.key == key                      // Если ключ совпадает
           delete(i)                        // удаляем и с этого уровня

Для того, чтобы удалить элемент с ключом [math]key[/math] из списка с пропусками [math]list[/math] достаточно вызвать функцию [math]\mathtt{erase}[/math] следующим образом:

   erase(list.head, key)

Применение

Список с пропусками применяется во многих приложениях, поскольку имеет ряд преимуществ.

1. Быстрая вставка элемента, поскольку не требуется каким-либо образом изменять другие элементы (только предыдущий элемент)
2. Проще реализовать, чем сбалансированные деревья или хеш-таблицы
3. Следующий элемент достаётся за [math]O(1)[/math]
4. Легко модифицировать под различные задачи

См. также

• Список
• Рандомизированное бинарное дерево поиска
• Поисковые структуры данных
• Skip quadtree
• Skip graph — структура данных, основанная на списке с пропусками

Источники информации

• Википедия — списки с пропусками
• Wikipedia — skip list
• igoro.com — Skip lists are fascinating
• springer.com — The interval skip list