Генерация дипфейков с помощью нейронных сетей — различия между версиями
Vshutov (обсуждение | вклад) |
Vshutov (обсуждение | вклад) |
||
| Строка 7: | Строка 7: | ||
Задача замены лиц или генерация Deepfake изображений состоит в том, чтобы перенести лицо с исходного (source) изображения на нужное (target) изображение. Такой перенос должен быть бесшовным и незаметным человеческому глазу. | Задача замены лиц или генерация Deepfake изображений состоит в том, чтобы перенести лицо с исходного (source) изображения на нужное (target) изображение. Такой перенос должен быть бесшовным и незаметным человеческому глазу. | ||
| − | Одним из этапов замены является реконструкция лица. Реконструкция лица заключается в изменении лица из | + | Одним из этапов замены является реконструкция лица. Реконструкция лица заключается в изменении лица из исходного изображения, так чтобы мимика и любая лицевая геометрия была соблюдена и соответствовала нужному изображению. |
| − | Методы, решавшие данную задачу в прошлом, были основаны на детектировании ключевых точек лица и далее используя данные точки, с помощью триангуляции Делоне строилась сетка(меш) лица и все треугольники из | + | Методы, решавшие данную задачу в прошлом, были основаны на детектировании ключевых точек лица и далее используя данные точки, с помощью триангуляции Делоне строилась сетка(меш) лица и все треугольники из исходного изображения масштабировались в соответствии с нужным изображением. В основе современных алгоритмов лежат Генеративно-Состязательные сети с различными модификациями. |
| − | Так же некоторые из используемых методов основаны на попытке аппроксимации некого распределения признаков. Данные методы пытаются вычислить соответствующее распределение и переносят с помощью нейронных сетей эти скрытые представления. В результате генерируется новое фотореалистичное лицо, которое соответствует необходимым характеристикам и метрикам. Одним из известных алгоритмов в этой области является Face2Face<ref name=Face2Face>[http://www.graphics.stanford.edu/~niessner/thies2016face.html Face2Face]</ref>, метод вычисляет меш лица и с помощью алгоритма Морфа 3D модели лица(''англ. 3D morphable face model'')<ref name=3DmorphableFaceModel>[https://arxiv.org/pdf/1909.01815.pdf 3D Morphable Face Model]</ref> переносит геометрию. | + | Так же некоторые из используемых методов основаны на попытке аппроксимации некого распределения признаков. Данные методы пытаются вычислить соответствующее распределение и переносят с помощью нейронных сетей эти скрытые представления. В результате генерируется новое фотореалистичное лицо, которое соответствует необходимым характеристикам и метрикам. Одним из известных алгоритмов в этой области является Face2Face<ref name=Face2Face>[http://www.graphics.stanford.edu/~niessner/thies2016face.html Face2Face]</ref>, метод вычисляет меш лица и с помощью алгоритма Морфа 3D модели лица (''англ. 3D morphable face model'')<ref name=3DmorphableFaceModel>[https://arxiv.org/pdf/1909.01815.pdf 3D Morphable Face Model]</ref> переносит геометрию. |
Методам на основе Генеративно-состязательных сетей не требуется никакие многоуровневые эвристические методы, они берут исходное изображение и сразу делают перенос пропуская промежуточные шаги. | Методам на основе Генеративно-состязательных сетей не требуется никакие многоуровневые эвристические методы, они берут исходное изображение и сразу делают перенос пропуская промежуточные шаги. | ||
== Реконструкция лица и сегментация == | == Реконструкция лица и сегментация == | ||
| − | Первый этап рассматриваемого алгоритма состоит из двух шагов, сегментации лица в | + | Первый этап рассматриваемого алгоритма состоит из двух шагов, сегментации лица в нужных и исходных изображениях и изменении геометрии из исходного лица, чтобы оно соответствовало нужного геометрии лица. |
Имея изображение $I \in {\rm I\!R}^{3 \times H \times W}$ и тепловую карту лицевых точек соответствующего изображения $H(p) \in {\rm I\!R}^{N \times H \times W}, p \in {\rm I\!R}^{N \times D}$, где $N$ {{---}} число точек, $D$ {{---}} размерность точек, обычно она равна 2, а число точек не превышает 70, мы обучаем генератор, чтобы он делал трансформацию данной тепловой карты и входного изображения в изображение с необходимой нам геометрией $G_r : \{ {\rm I\!R}^{3 \times H \times W}, {\rm I\!R}^{N \times H \times W} \} \to {\rm I\!R}^{3 \times H \times W} $. | Имея изображение $I \in {\rm I\!R}^{3 \times H \times W}$ и тепловую карту лицевых точек соответствующего изображения $H(p) \in {\rm I\!R}^{N \times H \times W}, p \in {\rm I\!R}^{N \times D}$, где $N$ {{---}} число точек, $D$ {{---}} размерность точек, обычно она равна 2, а число точек не превышает 70, мы обучаем генератор, чтобы он делал трансформацию данной тепловой карты и входного изображения в изображение с необходимой нам геометрией $G_r : \{ {\rm I\!R}^{3 \times H \times W}, {\rm I\!R}^{N \times H \times W} \} \to {\rm I\!R}^{3 \times H \times W} $. | ||
| − | Пусть $v_s, v_t \in {\rm I\!R}^{70 \times 3}$ и $e_s, e_t \in {\rm I\!R}^{3}$ будут трёхмерными ключевыми лицевыми точками лица и углами Эйлера<ref name=euler>[https://ru.wikipedia.org/wiki/%D0%A3%D0%B3%D0%BB%D1%8B_%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0 Углы Эйлера]</ref> в соответствии к $F_s$ и $F_t$, где $F_s$ {{---}} лицо с | + | Пусть $v_s, v_t \in {\rm I\!R}^{70 \times 3}$ и $e_s, e_t \in {\rm I\!R}^{3}$ будут трёхмерными ключевыми лицевыми точками лица и углами Эйлера<ref name=euler>[https://ru.wikipedia.org/wiki/%D0%A3%D0%B3%D0%BB%D1%8B_%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0 Углы Эйлера]</ref> в соответствии к $F_s$ и $F_t$, где $F_s$ {{---}} лицо с исходного изображение, $F_t$ {{---}} лицо с нужного изображение. Тогда мы построим 2D проекцию $p_j$ интерполируя между $e_s$ и $e_t$ и центроидами $v_s$ и $v_t$, и используя промежуточные точки мы обратно спроецируем $v_s$ на $I_s$. |
Другими словами алгоритм реконструкции является рекурсивным для каждой итерации: | Другими словами алгоритм реконструкции является рекурсивным для каждой итерации: | ||
| − | $I_{r_{j}}, S_{r_{j}} = G_r(I_{r_{j - 1}};H(p_j)), I_{r_{0}} = I_s, i < j < n$ | + | $I_{r_{j}}, S_{r_{j}} = G_r(I_{r_{j - 1}};H(p_j)), I_{r_{0}} = I_s, i < j < n$. |
| − | Наша модель $G_r$ имеет двы выхода. Первый выход выдает изображение с перенесенной геометрией, второй {{---}} маску для сегментации. Так же стоить заметить, что маска для сегментации | + | Наша модель $G_r$ имеет двы выхода. Первый выход выдает изображение с перенесенной геометрией, второй {{---}} маску для сегментации. Так же стоить заметить, что маска для сегментации состоит из трех классов, кожи, прически и фона. Такой подход позволяет увеличить точность всего процесса переноса. |
| − | + | Генераторы обучаются с помощью следующих функций потерь: | |
| − | $\displaystyle Loss(G_r) = \lambda_{stepwise} Loss_{rec}(I_{r_{n}}, I_{t}) + \lambda_{rec}Loss_{rec}(I_{r}, I_{t}) + \lambda_{adv}Loss_{adv} + \lambda_{seg}Loss_{pixel}(S_r, S_t)$ | + | $\displaystyle Loss(G_r) = \lambda_{stepwise} Loss_{rec}(I_{r_{n}}, I_{t}) + \lambda_{rec}Loss_{rec}(I_{r}, I_{t}) + \lambda_{adv}Loss_{adv} + \lambda_{seg}Loss_{pixel}(S_r, S_t)$. |
| − | $\displaystyle Loss(G_s) = Loss_{CE} + \lambda_{reenact}Loss_{pixel}(S_t, S_{t} {r})$ | + | $\displaystyle Loss(G_s) = Loss_{CE} + \lambda_{reenact}Loss_{pixel}(S_t, S_{t} {r})$. |
| − | $\displaystyle Loss_{perc}(x, y) = \sum_{i = 1}^{n} \frac{1}{C_i H_i W_i} || F_i(x) - F_i(y) ||_1 $ | + | $\displaystyle Loss_{perc}(x, y) = \sum_{i = 1}^{n} \frac{1}{C_i H_i W_i} || F_i(x) - F_i(y) ||_1 $. |
| − | $\displaystyle Loss_{pixel}(x, y) = || x - y ||_1 $ | + | $\displaystyle Loss_{pixel}(x, y) = || x - y ||_1 $. |
| − | $\displaystyle Loss_{rec}(x, y) = \lambda_{perc} Loss_{perc}(x, y) + \lambda_{pixel} Loss_{pixel}(x, y)$ | + | $\displaystyle Loss_{rec}(x, y) = \lambda_{perc} Loss_{perc}(x, y) + \lambda_{pixel} Loss_{pixel}(x, y)$. |
| − | $\displaystyle Loss_{adv}(G, D) = \min_{G} \max_{D_1, ..., D_n} \sum_{i = 1}^{n} Loss_{GAN}(G, D_i)$ | + | $\displaystyle Loss_{adv}(G, D) = \min_{G} \max_{D_1, ..., D_n} \sum_{i = 1}^{n} Loss_{GAN}(G, D_i)$. |
| − | $\displaystyle Loss_{GAN}(G, D) = \mathbb{E}_{(x, y)}[\log D(x, y)] + \mathbb{E}_{x} [\log(1 - D(x, G(x)))]$ | + | $\displaystyle Loss_{GAN}(G, D) = \mathbb{E}_{(x, y)}[\log D(x, y)] + \mathbb{E}_{x} [\log(1 - D(x, G(x)))]$. |
| Строка 48: | Строка 48: | ||
Имея множество исходных изображения $\{ I_{s_0}, ..., I_{s_{n}} \}$, углов Эйлера $ \{e_1, ..., e_n \}$ лиц $\{ F_{s_{0}}, ..., F_{s_{n}} \}$ строится карта внешнего вида (appearance map). | Имея множество исходных изображения $\{ I_{s_0}, ..., I_{s_{n}} \}$, углов Эйлера $ \{e_1, ..., e_n \}$ лиц $\{ F_{s_{0}}, ..., F_{s_{n}} \}$ строится карта внешнего вида (appearance map). | ||
Строится она следующим образом. | Строится она следующим образом. | ||
| − | В начале соответствующие углы Эйлера проецируются на плоскость. С помощью K-D дерева <ref name=kd>[https://neerc.ifmo.ru/wiki/index.php?title=%D0%9A-d_%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D1%8C%D1%8F_%D0%B8_%D0%BF%D0%B5%D1%80%D0%B5%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%82%D0%BE%D1%87%D0%B5%D0%BA_%D0%B2_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%BB%D1%8C%D0%BD%D0%BE%D0%BC_%D0%BF%D1%80%D1%8F%D0%BC%D0%BE%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B5_(%D1%81%D1%82%D0%B0%D1%82%D0%B8%D0%BA%D0%B0) K-D tree]</ref> точки в пространстве сегментируются и удаляются слишком близкие по расстоянию, поскольку они не несут в себе много полезной информации, а вычислительная сложность разительно увеличивается. Используя оставшиеся точки строим меш лица, используя триангуляцию Делоне<ref name=Delaunay>[ | + | В начале соответствующие углы Эйлера проецируются на плоскость. С помощью K-D дерева <ref name=kd>[https://neerc.ifmo.ru/wiki/index.php?title=%D0%9A-d_%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D1%8C%D1%8F_%D0%B8_%D0%BF%D0%B5%D1%80%D0%B5%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%82%D0%BE%D1%87%D0%B5%D0%BA_%D0%B2_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%BB%D1%8C%D0%BD%D0%BE%D0%BC_%D0%BF%D1%80%D1%8F%D0%BC%D0%BE%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B5_(%D1%81%D1%82%D0%B0%D1%82%D0%B8%D0%BA%D0%B0) K-D tree]</ref> точки в пространстве сегментируются и удаляются слишком близкие по расстоянию, поскольку они не несут в себе много полезной информации, а вычислительная сложность разительно увеличивается. Используя оставшиеся точки строим меш лица, используя триангуляцию Делоне<ref name=Delaunay>[http://neerc.ifmo.ru/wiki/index.php?title=%D0%A2%D1%80%D0%B8%D0%B0%D0%BD%D0%B3%D1%83%D0%BB%D1%8F%D1%86%D0%B8%D1%8F_%D0%94%D0%B5%D0%BB%D0%BE%D0%BD%D0%B5 Триангуляция Делоне]</ref>. |
Для каждого угла $e_t$ лица $F_t$, точки $x_t$ мы ищем треугольник $T$ соответствующий данной точке. | Для каждого угла $e_t$ лица $F_t$, точки $x_t$ мы ищем треугольник $T$ соответствующий данной точке. | ||
Пусть $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}$ будут трисом(треугольником) $T$ и $I_{s_{i_{1}}}, I_{s_{i_{2}}}, I_{s_{i_{3}}}$ {{---}} соответствующие лица. Необходимо вычислить барицентрические координаты<ref name=bari>[https://ru.wikipedia.org/wiki/%D0%91%D0%B0%D1%80%D0%B8%D1%86%D0%B5%D0%BD%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82%D1%8B Барицентрические координаты]</ref> $\lambda_{1}, \lambda_{2}, \lambda_{3}$ от $x_t$ относительно $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}$. Тогда результат интерполяции: | Пусть $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}$ будут трисом(треугольником) $T$ и $I_{s_{i_{1}}}, I_{s_{i_{2}}}, I_{s_{i_{3}}}$ {{---}} соответствующие лица. Необходимо вычислить барицентрические координаты<ref name=bari>[https://ru.wikipedia.org/wiki/%D0%91%D0%B0%D1%80%D0%B8%D1%86%D0%B5%D0%BD%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82%D1%8B Барицентрические координаты]</ref> $\lambda_{1}, \lambda_{2}, \lambda_{3}$ от $x_t$ относительно $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}$. Тогда результат интерполяции: | ||
| Строка 59: | Строка 59: | ||
== Вписывание лица == | == Вписывание лица == | ||
| − | Поскольку из-за разницы в углах поворота или разной прически сегментированные маски | + | Поскольку из-за разницы в углах поворота или разной прически сегментированные маски нужных и исходных изображений могут отличаться видимыми регионами. Например, у одной маски сегментации длинная прическа, которая закрывает пол лица, а у второй маски сегментации класс волос отсутствует. Поэтому нам необходимо "дорисовать" или "стереть" участки, которые не могут быть перенесены напрямую. |
Чтобы решить данную задачу мы обучим еще одну модель $G_c$. $G_c$ принимает в себя лицо $F_s$, такое что все необходимые участки будут дорисованы, а ненужные удалены. | Чтобы решить данную задачу мы обучим еще одну модель $G_c$. $G_c$ принимает в себя лицо $F_s$, такое что все необходимые участки будут дорисованы, а ненужные удалены. | ||
| − | Функция потерь такой сети | + | Функция потерь такой сети {{---}}} |
| − | $\displaystyle Loss(G_c) = \lambda_{rec}Loss_{rec}(I_c, I_t) + \lambda_{adv}Loss_{adv}$ | + | $\displaystyle Loss(G_c) = \lambda_{rec}Loss_{rec}(I_c, I_t) + \lambda_{adv}Loss_{adv}$. |
== Отрисовка полученного лица == | == Отрисовка полученного лица == | ||
| − | На самом последнем шаге мы уже имеем лицо, которое правильно повернуто и на нем присутствуют только регионы лица, что и на нужном нам изображении. Нам остается только применить цветокоррекцию и минимальные правки чтобы отрисованное лицо выглядело натурально. | + | На самом последнем шаге мы уже имеем лицо, которое правильно повернуто {{---}} и на нем присутствуют только регионы лица, что и на нужном нам изображении. Нам остается только применить цветокоррекцию и минимальные правки чтобы {{---}} отрисованное лицо выглядело натурально. |
Пусть $I_t$ будет исходным лицом, а $I_{r} {t}$ будет нужным нам лицом для переноса и $S_t$ маской сегментации. Тогда используя уравнение Пуассона <ref name=Poisson>[https://en.wikipedia.org/wiki/Poisson%27s_equation Уравнение Пуассона]</ref>, мы можем выполнить цветокоррекцию следующим образом | Пусть $I_t$ будет исходным лицом, а $I_{r} {t}$ будет нужным нам лицом для переноса и $S_t$ маской сегментации. Тогда используя уравнение Пуассона <ref name=Poisson>[https://en.wikipedia.org/wiki/Poisson%27s_equation Уравнение Пуассона]</ref>, мы можем выполнить цветокоррекцию следующим образом | ||
| − | $\displaystyle P(I_t;I_{r} {t};S_t) = arg min ||\nabla f - \nabla I {t}_{r}|| {2}_{2}$ | + | $\displaystyle P(I_t;I_{r} {t};S_t) = arg min ||\nabla f - \nabla I {t}_{r}||^{2}_{2}$ |
$\displaystyle f(i, j) = I_t(i, j), \forall S_t(i, j) = 0$ | $\displaystyle f(i, j) = I_t(i, j), \forall S_t(i, j) = 0$ | ||
| Строка 85: | Строка 85: | ||
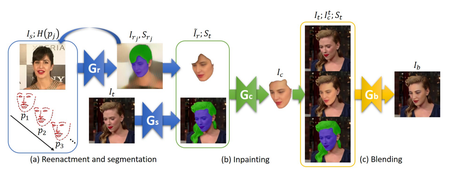
[[Файл:Deep_fake_pipeline.png|thumb|right|450px|Рисунок 4. Общая схема алгоритма]] | [[Файл:Deep_fake_pipeline.png|thumb|right|450px|Рисунок 4. Общая схема алгоритма]] | ||
| − | В качестве обучающего множества можно использовать множество дата сетов с размеченными лицами, одним из таких служит IJB-C <ref name=ijbc>[https://noblis.org/wp-content/uploads/2018/03/icb2018.pdf IJB-C]</ref>. На нем обучается генератор $G_r$. Данный дата сет состоит из более чем $11$ тысяч видео, $5500$ из которых высокого качества. | + | В качестве обучающего множества можно использовать множество дата сетов с размеченными лицами, одним из таких служит IJB-C <ref name=ijbc>[https://noblis.org/wp-content/uploads/2018/03/icb2018.pdf IJB-C]</ref>. На нем обучается генератор $G_r$. Данный дата сет состоит из более чем $11$ тысяч видео, $5500$ из которых высокого качества. При обучении кадры из $I_s$ и $I_t$ берутся из двух случайных видео. Так же для начального шага нам был необходим perceptual loss<ref name=perceptual>[https://arxiv.org/abs/1603.08155 Perceptual Losses for Real-Time Style Transfer and Super-Resolution]</ref>, он может быть получен, обучив VGG-19<ref name=vgg>[https://arxiv.org/abs/1409.1556 Very Deep Convolutional Networks for Large-Scale Image Recognition]</ref> модель или взяв готовую обученную на ImageNet<ref name=imagenet>[http://www.image-net.org/ ImageNet]</ref> или VGGFace2<ref name=vggface2>[https://arxiv.org/abs/1710.08092 VGGFace2: A dataset for recognising faces across pose and age]</ref>, второй дата сет предпочтительный, поскольку для его обучения используются только лица. |
В качестве оптимизатора рекомендуется использовать Adam<ref name=adam>[https://arxiv.org/abs/1412.6980 Adam: A Method for Stochastic Optimization]</ref> с параметром скорости обучения (learning rate) = $0.0002$. | В качестве оптимизатора рекомендуется использовать Adam<ref name=adam>[https://arxiv.org/abs/1412.6980 Adam: A Method for Stochastic Optimization]</ref> с параметром скорости обучения (learning rate) = $0.0002$. | ||
$\lambda_{perc} = 1, \lambda_{pixel} = 0.1, \lambda_{adv} = 0.001, \lambda_{seg} = 0.1, \lambda_{stepwise} = 1$, параметр $\lambda_{reenact}$ возрастает линейно от $0-1$. | $\lambda_{perc} = 1, \lambda_{pixel} = 0.1, \lambda_{adv} = 0.001, \lambda_{seg} = 0.1, \lambda_{stepwise} = 1$, параметр $\lambda_{reenact}$ возрастает линейно от $0-1$. | ||
| − | + | Время обучения генератора $G_s$ занимает 6 часов, все остальные сети учатся 2-3 дня на восьми Nvidia Tesla V100. | |
Скорость работы всего алгоритма составляет около ~$10$ fps на Nvidia Tesla V100. | Скорость работы всего алгоритма составляет около ~$10$ fps на Nvidia Tesla V100. | ||
| Строка 101: | Строка 101: | ||
* [[Генерация объектов]] | * [[Генерация объектов]] | ||
* [[К-d деревья и перечисление точек в произвольном прямоугольнике (статика)]] | * [[К-d деревья и перечисление точек в произвольном прямоугольнике (статика)]] | ||
| + | * [[Триангуляция Делоне]] | ||
==Примечания== | ==Примечания== | ||
Версия 10:33, 12 января 2021
Дипфейк (англ. Deepfake) — результат работы ряда алгоритмов для синтеза изображений человеческого лица или голоса. Алгоритмы, применяемые для решения данной задачи основаны на Порождающе-состязательных сетях. Современные алгоритмы позволяют генерировать не только лицо человека, но и его голос. C таким примером можно ознакомится по ссылке Home Stallone DeepFake
Содержание
Введение
Задача замены лиц или генерация Deepfake изображений состоит в том, чтобы перенести лицо с исходного (source) изображения на нужное (target) изображение. Такой перенос должен быть бесшовным и незаметным человеческому глазу. Одним из этапов замены является реконструкция лица. Реконструкция лица заключается в изменении лица из исходного изображения, так чтобы мимика и любая лицевая геометрия была соблюдена и соответствовала нужному изображению. Методы, решавшие данную задачу в прошлом, были основаны на детектировании ключевых точек лица и далее используя данные точки, с помощью триангуляции Делоне строилась сетка(меш) лица и все треугольники из исходного изображения масштабировались в соответствии с нужным изображением. В основе современных алгоритмов лежат Генеративно-Состязательные сети с различными модификациями. Так же некоторые из используемых методов основаны на попытке аппроксимации некого распределения признаков. Данные методы пытаются вычислить соответствующее распределение и переносят с помощью нейронных сетей эти скрытые представления. В результате генерируется новое фотореалистичное лицо, которое соответствует необходимым характеристикам и метрикам. Одним из известных алгоритмов в этой области является Face2Face[1], метод вычисляет меш лица и с помощью алгоритма Морфа 3D модели лица (англ. 3D morphable face model)[2] переносит геометрию. Методам на основе Генеративно-состязательных сетей не требуется никакие многоуровневые эвристические методы, они берут исходное изображение и сразу делают перенос пропуская промежуточные шаги.
Реконструкция лица и сегментация
Первый этап рассматриваемого алгоритма состоит из двух шагов, сегментации лица в нужных и исходных изображениях и изменении геометрии из исходного лица, чтобы оно соответствовало нужного геометрии лица. Имея изображение $I \in {\rm I\!R}^{3 \times H \times W}$ и тепловую карту лицевых точек соответствующего изображения $H(p) \in {\rm I\!R}^{N \times H \times W}, p \in {\rm I\!R}^{N \times D}$, где $N$ — число точек, $D$ — размерность точек, обычно она равна 2, а число точек не превышает 70, мы обучаем генератор, чтобы он делал трансформацию данной тепловой карты и входного изображения в изображение с необходимой нам геометрией $G_r : \{ {\rm I\!R}^{3 \times H \times W}, {\rm I\!R}^{N \times H \times W} \} \to {\rm I\!R}^{3 \times H \times W} $. Пусть $v_s, v_t \in {\rm I\!R}^{70 \times 3}$ и $e_s, e_t \in {\rm I\!R}^{3}$ будут трёхмерными ключевыми лицевыми точками лица и углами Эйлера[3] в соответствии к $F_s$ и $F_t$, где $F_s$ — лицо с исходного изображение, $F_t$ — лицо с нужного изображение. Тогда мы построим 2D проекцию $p_j$ интерполируя между $e_s$ и $e_t$ и центроидами $v_s$ и $v_t$, и используя промежуточные точки мы обратно спроецируем $v_s$ на $I_s$. Другими словами алгоритм реконструкции является рекурсивным для каждой итерации:
$I_{r_{j}}, S_{r_{j}} = G_r(I_{r_{j - 1}};H(p_j)), I_{r_{0}} = I_s, i < j < n$.
Наша модель $G_r$ имеет двы выхода. Первый выход выдает изображение с перенесенной геометрией, второй — маску для сегментации. Так же стоить заметить, что маска для сегментации состоит из трех классов, кожи, прически и фона. Такой подход позволяет увеличить точность всего процесса переноса.
Генераторы обучаются с помощью следующих функций потерь:
$\displaystyle Loss(G_r) = \lambda_{stepwise} Loss_{rec}(I_{r_{n}}, I_{t}) + \lambda_{rec}Loss_{rec}(I_{r}, I_{t}) + \lambda_{adv}Loss_{adv} + \lambda_{seg}Loss_{pixel}(S_r, S_t)$.
$\displaystyle Loss(G_s) = Loss_{CE} + \lambda_{reenact}Loss_{pixel}(S_t, S_{t} {r})$.
$\displaystyle Loss_{perc}(x, y) = \sum_{i = 1}^{n} \frac{1}{C_i H_i W_i} || F_i(x) - F_i(y) ||_1 $.
$\displaystyle Loss_{pixel}(x, y) = || x - y ||_1 $.
$\displaystyle Loss_{rec}(x, y) = \lambda_{perc} Loss_{perc}(x, y) + \lambda_{pixel} Loss_{pixel}(x, y)$.
$\displaystyle Loss_{adv}(G, D) = \min_{G} \max_{D_1, ..., D_n} \sum_{i = 1}^{n} Loss_{GAN}(G, D_i)$.
$\displaystyle Loss_{GAN}(G, D) = \mathbb{E}_{(x, y)}[\log D(x, y)] + \mathbb{E}_{x} [\log(1 - D(x, G(x)))]$.
Где $G_r$ — генератор переноса геометрии, $G_s$ — генератор сегментации лица.
Перенос сгенерированного лица
Далее после того, как мы получили изображение лица с нужной нам геометрией необходимо перенести его на исходное изображение. Общеизвестным способ переноса геометрии одной текстуры на другую является перенос полигонов из сеток двух мешей [4]. Однако существуют более современные способы. Имея множество исходных изображения $\{ I_{s_0}, ..., I_{s_{n}} \}$, углов Эйлера $ \{e_1, ..., e_n \}$ лиц $\{ F_{s_{0}}, ..., F_{s_{n}} \}$ строится карта внешнего вида (appearance map). Строится она следующим образом. В начале соответствующие углы Эйлера проецируются на плоскость. С помощью K-D дерева [5] точки в пространстве сегментируются и удаляются слишком близкие по расстоянию, поскольку они не несут в себе много полезной информации, а вычислительная сложность разительно увеличивается. Используя оставшиеся точки строим меш лица, используя триангуляцию Делоне[6]. Для каждого угла $e_t$ лица $F_t$, точки $x_t$ мы ищем треугольник $T$ соответствующий данной точке. Пусть $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}$ будут трисом(треугольником) $T$ и $I_{s_{i_{1}}}, I_{s_{i_{2}}}, I_{s_{i_{3}}}$ — соответствующие лица. Необходимо вычислить барицентрические координаты[7] $\lambda_{1}, \lambda_{2}, \lambda_{3}$ от $x_t$ относительно $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}$. Тогда результат интерполяции:
$\displaystyle I_r = \sum_{k=1}^{3} \lambda_k G_r(I_{s_{i_{k}}}; H(p_t))$
Где $p_t$ 2D ключевая точка лица $F_t$.
Вписывание лица
Поскольку из-за разницы в углах поворота или разной прически сегментированные маски нужных и исходных изображений могут отличаться видимыми регионами. Например, у одной маски сегментации длинная прическа, которая закрывает пол лица, а у второй маски сегментации класс волос отсутствует. Поэтому нам необходимо "дорисовать" или "стереть" участки, которые не могут быть перенесены напрямую. Чтобы решить данную задачу мы обучим еще одну модель $G_c$. $G_c$ принимает в себя лицо $F_s$, такое что все необходимые участки будут дорисованы, а ненужные удалены. Функция потерь такой сети —}
$\displaystyle Loss(G_c) = \lambda_{rec}Loss_{rec}(I_c, I_t) + \lambda_{adv}Loss_{adv}$.
Отрисовка полученного лица
На самом последнем шаге мы уже имеем лицо, которое правильно повернуто — и на нем присутствуют только регионы лица, что и на нужном нам изображении. Нам остается только применить цветокоррекцию и минимальные правки чтобы — отрисованное лицо выглядело натурально.
Пусть $I_t$ будет исходным лицом, а $I_{r} {t}$ будет нужным нам лицом для переноса и $S_t$ маской сегментации. Тогда используя уравнение Пуассона [8], мы можем выполнить цветокоррекцию следующим образом
$\displaystyle P(I_t;I_{r} {t};S_t) = arg min ||\nabla f - \nabla I {t}_{r}||^{2}_{2}$
$\displaystyle f(i, j) = I_t(i, j), \forall S_t(i, j) = 0$
$\nabla$ — оператор взятия градиента.
Данное уравнения используется в качестве функции для оптимизации нашего генератора $G_b$, который и будет заниматься отрисовкой финальной версии нашего Deepfake изображения.
$\displaystyle Loss(G_b) = \lambda_{rec}Loss_{rec}(I_t;I_{r} {t};S_t), P(I_t;I_{r} {t};S_t)) + \lambda_{adv}Loss_{adv}$
Данные для обучения и процесс обучения
В качестве обучающего множества можно использовать множество дата сетов с размеченными лицами, одним из таких служит IJB-C [9]. На нем обучается генератор $G_r$. Данный дата сет состоит из более чем $11$ тысяч видео, $5500$ из которых высокого качества. При обучении кадры из $I_s$ и $I_t$ берутся из двух случайных видео. Так же для начального шага нам был необходим perceptual loss[10], он может быть получен, обучив VGG-19[11] модель или взяв готовую обученную на ImageNet[12] или VGGFace2[13], второй дата сет предпочтительный, поскольку для его обучения используются только лица. В качестве оптимизатора рекомендуется использовать Adam[14] с параметром скорости обучения (learning rate) = $0.0002$. $\lambda_{perc} = 1, \lambda_{pixel} = 0.1, \lambda_{adv} = 0.001, \lambda_{seg} = 0.1, \lambda_{stepwise} = 1$, параметр $\lambda_{reenact}$ возрастает линейно от $0-1$.
Время обучения генератора $G_s$ занимает 6 часов, все остальные сети учатся 2-3 дня на восьми Nvidia Tesla V100. Скорость работы всего алгоритма составляет около ~$10$ fps на Nvidia Tesla V100.
Реализация
Готовую реализацию можно найти по ссылке FSGAN, так же существуют альтернативные, но не менее продвинутые алгоритмы DeepFaceLab, faceswap.
См. также
- Generative Adversarial Nets (GAN)
- Порождающие модели
- Нейронные сети, перцептрон
- Генерация объектов
- К-d деревья и перечисление точек в произвольном прямоугольнике (статика)
- Триангуляция Делоне
Примечания
- ↑ Face2Face
- ↑ 3D Morphable Face Model
- ↑ Углы Эйлера
- ↑ Face Swap
- ↑ K-D tree
- ↑ Триангуляция Делоне
- ↑ Барицентрические координаты
- ↑ Уравнение Пуассона
- ↑ IJB-C
- ↑ Perceptual Losses for Real-Time Style Transfer and Super-Resolution
- ↑ Very Deep Convolutional Networks for Large-Scale Image Recognition
- ↑ ImageNet
- ↑ VGGFace2: A dataset for recognising faces across pose and age
- ↑ Adam: A Method for Stochastic Optimization
Источники информации
- Nirkin, Yuval, Yosi Keller, and Tal Hassner. "FSGAN: Subject agnostic face swapping and reenactment." In Proceedings of the IEEE international conference on computer vision, pp. 7184-7193. 2019.
- Nirkin, Y., Masi, I., Tuan, A. T., Hassner, T., & Medioni, G. (2018, May). On face segmentation, face swapping, and face perception. In 2018 13th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2018) (pp. 98-105). IEEE.