Динамическое программирование

<wikitex>

Оптимальность для подзадач

Важнейшее свойство задач, которое позволяет решать их с помощью динамического программирования это оптимальность для подзадач. В зависимости от формулировки задачи, будь то динамическое программирование на отрезке, на префиксе, на дереве, термин оптимальности для подзадач может быть различным.

Определение

Определение:

Принцип оптимальности для подзадач – важнейшее свойство задачи, формулирующееся следующим образом: «Если есть оптимальное решение для некоторой подзадачи, которая возникает в процессе решения задачи, то именно его нужно использовать для решения задачи в целом»

Рассмотрим принцип оптимальности для динамического программирования на префиксе:

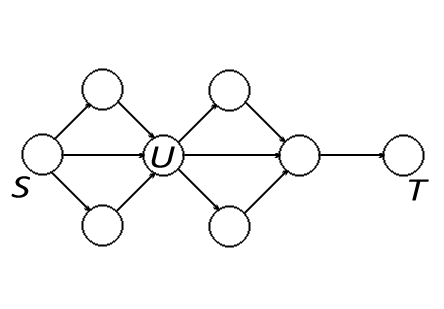
Префикс оптимального пути $S \rightsquigarrow U$ является оптимальным путём $S \rightsquigarrow U$. Требуется дойти до $T$. Есть какой-то префикс, оптимальный путь проходит через $U$. Рассмотрим префикс $\Delta U$, пусть он неоптимальный. Это значит, что есть более оптимальный путь. Тогда заменим этот префикс на более оптимальный путь до $U$, а путь $U \rightsquigarrow T$ добавим в конец. Получится более оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется. </wikitex>

Ссылки

• Лекция 10.11.2011
• Жадный алгоритм
• Т. Кормен. «Алгоритмы. Построение и анализ» (Глава 15.3)