Турниры

Определение:

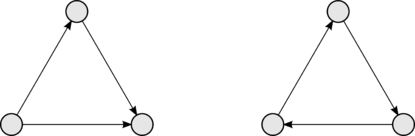
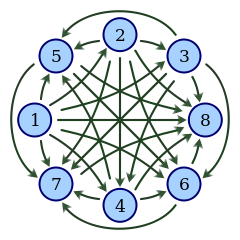
Турнир (англ. Tournament) — ориентированный граф, между любой парой различных вершин которого есть ровно одно ориентированное ребро.

Турниром из [math]n[/math] вершин можно изобразить исход игры между [math]n[/math] людьми, где каждый играет с каждым. Тогда ребро будет ориентировано от выигравшего человека к проигравшему.

Турниры из трех вершин

Свойства турниров

Оценка количества турниров в графе

Если в турнире опустить ориентацию ребер, то мы получим полный граф. А так как существует два варианта ориентации каждого ребра, то количество турниров в графе из [math]n[/math] вершин равно [math]2^{\frac{n\cdot(n-1)}{2}}[/math].

Транзитивность

Транзитивный турнир с 8 вершинами

Турнир, в котором [math](a, b)\land(b, c) \Rightarrow (a, c)[/math], называется транзитивным. В транзитивном турнире вершины могут быть полностью упорядочены в порядке достижимости.

Теорема:

Пусть [math]T=\langle V, E\rangle[/math] — турнир, [math]\vert V \vert = n[/math]. Тогда следующие утверждения эквивалентны: [math]T[/math] транзитивен; [math]T[/math] не содержит циклов длины [math]3[/math]; [math]T[/math] ациклический; множества, составленные из [math]\deg^{-}[/math] или [math]\deg^{+}[/math] для каждой вершины [math]T[/math], есть [math]\{ 0, 1, 2,..., n - 1\} [/math]; [math]T[/math] содержит ровно один гамильтонов путь.

Доказательство:

[math]\triangleright[/math]

[math]1 \Rightarrow 2:[/math] Пусть существует цикл длины [math]3: (u, v), (v, w), (w, u). [/math] Однако по транзитивности должно существовать ребро [math](u, w)[/math], т.е. между [math]u, w[/math] есть [math]2[/math] противонаправенных ребра, что невозможно по определению турнира. [math]2 \Rightarrow 3:[/math] Пусть в графе содержится цикл длины [math]k \neq 3[/math]. Это не может быть цикл длины [math]2[/math] (противоречит определению турнира). Обозначим его вершины в порядке обхода [math]v_1, v_2, \ldots, v_k, k \geqslant 4[/math]. Заметим, что т.к. нет циклов длины [math]3[/math], выполнена транзитивность (в противном случае существовали бы ребра [math](u, v), (v, w), (w, u)[/math]). Докажем по индукции, что существует ребро [math](v_1, v_{k - 1}).[/math] База индукции [math]k = 3[/math]: [math](v_1, v_2) , (v_2, v_3) \in E \Rightarrow (v_1, v_3) \in E [/math] (по транзитивности). Переход индукции Пусть доказано для всех [math]i \lt k - 1[/math], что [math](v_1, v_i) \in E[/math], также известно, что [math](v_i, v_{i+1}) \in E[/math], тогда по транзитивности [math](v_1, v_{i+1}) \in E[/math]. Таким образом, в транзитивном турнире содержится цикл длины [math]3[/math] — противоречие (см. предыдущий пункт). [math]3 \Rightarrow 4: [/math] Обозначим множество значений степеней исхода как [math]Deg^{+}(T)[/math]. Докажем индукцией по n. База индукции [math]n = 1[/math]: верно, т.к. есть одна вершина степени [math]0[/math] Переход индукции Пусть доказано для [math]n - 1[/math]. В ациклическом графе существует сток [math]t, deg^{+}(t) = 0[/math]. Рассмотрим граф [math]T-t[/math]. [math]Deg^{+}(T - t) = \{0, 1, \ldots, n - 2\}[/math] . Т.к. из каждой [math]v \in V \setminus \{t\}[/math] ведет одно ребро в [math]t[/math], [math] Deg^{+}(T)=\{deg^{+}(t)\} \cup \{x + 1 \mid x \in Deg^{+}(T -t)\} = \{0, 1, \ldots, n - 1\}[/math], что и требовалось. Для степеней захода можно доказать аналогично, рассмотрев исток вместо стока. [math]4 \Rightarrow 5: [/math] По теореме Редеи-Камиона, в любом турнире есть гамильтонов путь, докажем единственность индукцией по [math]n[/math]. База индукции [math]n = 1[/math]: верно, путь из одной вершины. Переход индукции Рассмотрим вершину [math]s: deg^{-}(s) = 0[/math]. Она будет первой в гамильтоновом пути. Рассмотрим граф [math]T - s[/math], в нем существует единственный гамильтонов путь (по предположению), значит и в [math]T[/math] он будет единственным. [math]5 \Rightarrow 1: [/math] Пусть [math]P=\{v_1, v_2, \ldots, v_n\}[/math] — единственный гамильтонов путь. Пусть найдется [math]m[/math] — наименьший индекс такой, что в вершину [math]v_m[/math] идет ребро из вершины с большим индексом, а [math]v_k[/math] — вершина с наибольшим индексом, из которой ребро ведет в [math]v_m[/math]. Возможно несколько случаев: [math] m \neq 1, k \neq n: [/math] Из [math]v_{m -1}[/math] ведет ребро в [math]v_{m+1}[/math] (по минимальности [math]m[/math]), а из [math]v_m[/math] ведет ребро в [math]v_{k +1}[/math] (по максимальности [math]k[/math]). Тогда будет существовать еще один гамильтонов путь [math]P_1 = \{v_1, \ldots, v_{m-1}, v_{m+1}, \ldots, v_{k}, v_m, v_{k+1}, \ldots, v_n\}[/math]. [math] m \neq 1, k = n: [/math] [math]P_1 = \{v_1, \ldots, v_{m-1}, v_{m+1}, \ldots, v_{n}, v_m\}[/math]. [math] m = 1, k \neq n:[/math] [math]P_1 = \{v_2, \ldots, v_{k}, v_1, v_{k+1}\}[/math] [math] m = 1, k = n:[/math] [math]P_1 = \{v_2, \ldots, v_n, v_1\}[/math] Замечание Может достигаться равенство [math]m + 1 = n[/math], в этом случае нужно исключить из пути [math]2[/math] последовательных вхождения [math]v_n[/math]. Во всех случаях получаем противоречие с единственностью гамильтонова пути, значит не существует такого [math]m[/math], т.е [math](v_i, v_j) \in E \Leftrightarrow i \lt j[/math]. Значит [math]\forall i, j, k: 1 \leqslant i, j, k \leqslant n, (v_i, v_j) \in E \land (v_j, v_k) \in E \Rightarrow i \lt j \land j \lt k \Rightarrow (v_i, v_k) \in E [/math].

[math]\triangleleft[/math]

Теория Рамсея

Транзитивные турниры играют существенную роль в теории Рамсея, изучающей условия, при которых в произвольно формируемых математических объектах обязан появиться некоторый порядок. В частности, любой турнир с [math]n[/math] вершинами содержит транзитивный подтурнир с [math]1+\lfloor\log_2 n\rfloor[/math] вершинами. Для его построения выберем любую вершину [math]v[/math] как часть этого подтурнира и построим подтурнир рекурсивно на множестве либо входящих соседей вершины [math]v[/math], либо на множестве исходящих соседей, в зависимости от того, какое множество больше.

Конденсация

Конденсация любого турнира является транзитивным турниром. Таким образом, даже если турнир не является транзитивным, сильно связанные компоненты турнира могут быть полностью упорядочены.

Сильно связные турниры

Определение:

Турнир называется сильно связным, если из любой вершины существуют пути до всех других.

Определение:

Турнир называется гамильтоновым, если он содержит гамильтонов цикл.

Негамильтонов турнир

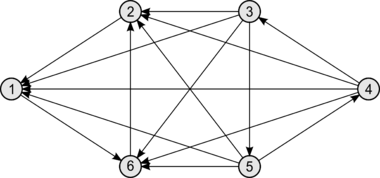
Не все турниры гамильтоновы. Определение не исключает существование вершины с [math]\deg^{-}[/math] или [math]\deg^{+}[/math] равной нулю — в первую нельзя войти, а из второй — выйти. Однако отсутствие таких вершин не означает, что турнир гамильтонов (пример — на рисунке справа).

Теорема Редеи-Камиона устанавливает два следующих факта:

1. Все турниры полугамильтоновы.
2. Турнир гамильтонов тогда и только тогда, когда он сильно связен.

См. также

• Гамильтоновы графы
• Теорема Редеи-Камиона
• Поиск гамильтонова цикла за [math]O(n\cdot log(n))[/math]

Источники информации

• Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — ISBN 5-93972-076-5
• Wikipedia — Турнир