Лемма Огдена

Лемма:

Для каждой контекстно-свободный грамматики [math]\Gamma =\langle \Sigma, N, S \in N, P \subset N^{+}\times (\Sigma\cup N)^{*}\rangle[/math] существует такое [math]n[/math], что для любого слова [math]\omega \in L(\Gamma)[/math], длины не менее [math]n[/math], и для любых выделенных в [math]\omega[/math] не менее [math]n[/math] позиций, то [math]\omega[/math] может быть представлено в виде [math]\omega=uvxyz[/math], причем: x содержит выделенную позицию либо [math]u[/math] и [math]v[/math], либо [math]y[/math] и [math]z[/math] обе содержат выделенные позиции; [math]vxy[/math] содержат не более [math]n[/math] выделенных позиций; существует [math]A \in L[/math], такой что [math]S \Rightarrow^{+} uAz \Rightarrow^{+} uvAyz \Rightarrow^{+} uvxyz[/math]

Доказательство:

[math]\triangleright[/math]

Введем следующие обозначения: [math]m = |N|[/math] и [math]l[/math] — длина самой длинной правой части правила из [math]P[/math]. Тогда в качестве [math]n[/math] возьмем [math]l^{2m + 3}[/math]. Рассмотрим дерево разбора [math]T[/math] для произвольного слова [math]\omega \in L(\Gamma)[/math], у которого [math]|\omega| \ge n[/math]. В силу выбора [math]n[/math] в [math]T[/math] будет по крайне мере один путь от корня до листа длины, не менее [math]2m + 3[/math]. Произвольным образом выделим в [math]\omega[/math] не менее [math]n[/math] позиций. Соответствующие этим позициям листья дерева [math]T[/math] будем называть выделенными. Пусть [math]v_1[/math] — корень [math]T[/math], а [math]v_{i + 1}[/math] — сын [math]v_i[/math], который имеет среди своих потомков наибольшее число выделенных листьев (если таких несколько, то [math]v_{i + 1}[/math] самый правый из них). Рассмотрим [math]v_1, v_2, ..., v_p[/math] — путь от корня до листа. Будем называть ветвящейся ту вершину, у которой по крайне мере два сына имеют выделенных потомков. Покажем по индукции, что если среди [math]v_1, v_2, ..., v_i[/math] вершин есть [math]k[/math] ветвящихся, то [math]v_{i + 1}[/math] имеет хотя бы [math]l^{2m + 3 - k}[/math] выделенных потомков. База индукции: [math]i = 0[/math]. Тогда [math]k = 0[/math] и [math]n_1[/math] имеет по крайне мере [math]n[/math] выделенных потомков, поскольку является корнем. Индукционный переход. Если [math]v_i[/math] не является ветвящейся вершиной, то [math]v_{i + 1}[/math] имеет такое же число ветвящихся потомков как и [math]v_i[/math]. Если [math]v_i[/math] — ветвящаяся вершина, то [math]v_{i + 1}[/math] имеет не более чем в [math]l[/math] раз меньшее число выделенных потомков. Поскольку [math]v_1[/math] имеет хотя бы [math]n = l^{2m + 3}[/math] выделенных потомков, то [math]v_1, v_2, ..., v_p[/math] содержит по крайне мере [math]2m + 3[/math] ветвящиеся вершин. Заметим, что [math]v_p[/math] — лист, поэтому [math]p \gt 2m + 3[/math]. 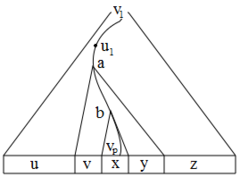Дерево вывода [math]T[/math] Будем называть [math]v_i[/math] левой ветвящейся вершиной, если ее сын, не принадлежащий пути [math]v_1, v_2, ..., v_p[/math], имеет выделенного потомка лежащего слева от [math]v_p[/math]. В противном случае назовем [math]v_i[/math] правой ветвящейся вершиной. Рассмотрим последние [math]2m + 3[/math] вершины принадлежащий пути [math]v_1, v_2, ..., v_p[/math]. Предположим, что хотя бы [math]m + 2[/math] вкршины левые ветвящиеся (случай, когда хотя бы [math]m + 2[/math] вершины правые ветвящиеся, разбирается аналогично). Пусть [math]u_1, u_2, ..., u_{m + 2}[/math] — последние [math]m + 2[/math] левые ветвящиеся вершины. Поскольку [math]m = |N|[/math], то среди них можно найти как минимум две вершины, соответствующие одному нетерменалу. Обозначим эти вершины [math]a[/math] и [math]b[/math], причем [math]b[/math] потомок [math]a[/math]. Тогда на рисунке показано как представить [math]\omega[/math] в требуемом виде. Условие (1) выполнено, поскольку [math]x[/math] содержит выделенную вершину, а именно [math]v_p[/math]. Очевидно, что условие(4) выполнено в силу предложенного разбиения [math]\omega[/math]. Кроме того, [math]u[/math] содержит выделенную вершину, а именно потомка некоторого сына вершины [math]u_1[/math]. Аналогично выделенный потомок некоторого сына вершины [math]a[/math] содержится в [math]v[/math]. Таким образом, условие (2) выполнено. Поскольку между [math]v_p[/math] и [math]a[/math] не более [math]2m + 3[/math] вершин, то вершина [math]a[/math] имеет не более [math]n[/math] выделенных потомков, поэтому условие (3) выполнено.

[math]\triangleleft[/math]