Динамика по поддеревьям
Содержание
Динамика по поддеревьям
Главной особенностью динамического программирования по поддеревьям является необходимость учитывать ответы в поддеревьях, т.к. они могут влиять на ответы в других поддеревьях. Рассмотрим для лучшего понимания динамики по поддеревьям задачу о максимальном взвешенном паросочетании в дереве.
Задача о максимальном взвешенном паросочетании на дереве
Формулировка
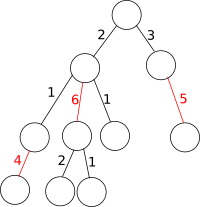
Пусть дано подвешенное за корень дерево, имеющее веса на каждом из его ребер. Необходимо выбрать такое множество ребер, чтобы сумма значений была максимальной, и при этом выбранные ребра не имели бы общих вершин. Т.е. необходимо решить задачу о максимальном взвешенном паросочетании.
Решение
Главное отличие этой задачи от других динамически решаемых — ответ в одном поддереве влияет на решение в остальных.
Рассмотрим наше первое состояние, когда еще не выбрана ни одна вершина. В этом случае мы можем сделать две вещи:
- Разрешить выбирать ребро из корня к ребенку.
- Запретить выбирать ребра из корня.
Если мы запрещаем, значит можем разрешить всем его детям выбрать ребро из своего корня к своим детям. В ином случае мы можем разрешить не всем детям, а только тем, которые не были выбраны ребром из корня.
Рекуррентная формула
Обозначим в качестве функцию, возвращающую ответ для поддерева с корнем . Если , то в этом поддереве мы разрешаем занимать корень, иначе нет. Обозначим вес ребра из в как
Заметим, что вторую формулу можно упростить:
Теперь наши формулы имеют вид:
Заметим, что с помощью этого преобразования мы сократили общее время вычисления с до .
Реализация
Заполним изначально массив dp[N][2] числом -1.
calculate(v, useRoot):
if dp[v][useRoot] != -1:
return dp[v][useRoot] //вернули уже посчитанное значение dp[vertex][root]
sum = 0
if useRoot == 0: //случай 1: не берем ребра из корня
for (для) всех u из множества детей v:
sum += calculate(u, 1)
dp[v][useRoot] = sum
else:
max1 = dp[v][0] //случай 2: берем какое-то ребро
for (для) всех x из множества детей v:
max1 = max(max1, calculate(x, 0) + calculate(vertex, 0) - calculate(x, 1) + w[v,x])
dp[v][useRoot] = max1
return dp[v][useRoot]