Алгоритм Бойера-Мура

Алгоритм Бойера-Мура, разработанный двумя учеными — Бойером (Robert S. Boyer) и Муром (J. Strother Moore), считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска подстроки в строке. Важной особенностью алгоритма является то, что он выполняет сравнения в шаблоне справа налево в отличии от многих других алгоритмов.

Алгоритм Бойера-Мура считается наиболее эффективным алгоритмом поиска шаблонов в стандартных приложениях и командах, таких как Ctrl+F в браузерах и текстовых редакторах.

Алгоритм

Алгоритм сравнивает символы шаблона [math]y[/math] справа налево, начиная с самого правого, один за другим с символами исходной строки [math]x[/math]. В случае несовпадения какого-либо символа (или полного совпадения всего шаблона) он использует две предварительно вычисляемых функций, чтобы сдвинуть позицию для начала сравнения вправо. Область определения одной из функций зависит линейно от размера алфавита [math]\Sigma[/math]

Пусть [math]|y|=n[/math], [math]|x|=m[/math] и [math]|\Sigma|=\sigma[/math]

Предположим, что в процессе сравнения возникает несовпадение между символом [math]x[i]=a[/math] шаблона и символом [math]y[i+j]=b[/math] исходного текста при проверке в позиции [math]j[/math]. Тогда [math]x[i+1 .. m-1]=y[i+j+1 .. j+m-1]=u[/math] и [math]x[i] \neq y[i+j][/math], т.е. [math]m - i - 1[/math] символов шаблона уже совпало.

Правило сдвига хорошего суффикса

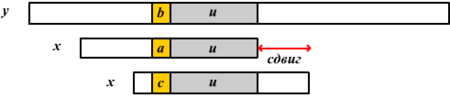
Если при сравнении текста и шаблона совпало один или больше символов, шаблон сдвигается в зависимости от того, какой суффикс совпал.

Если существует такая подстрока [math]u[/math], что она полностью входит в [math]x[/math] и идет справа от символа, отличного от [math]x[i][/math], то сдвиг идет на всю длину этого суффикса.

Сдвиг хорошего суффикса, вся подстрока [math]u[/math] полностью встречается справа от символа [math]c[/math], отличного от символа [math]a[/math].

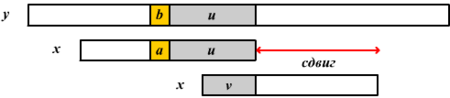
Если не существует такой подстроки, то смещение состоит в выравнивании самого длинного суффикса [math]v[/math] подстроки [math]y[i+j+1 .. j+m-1][/math] с соответствующим префиксом [math]x[/math].

Сдвиг хорошего суффикса, только суффикс подстроки [math]u[/math] повторно встречается в [math]x[/math].

Правило сдвига плохого символа

В таблице плохих символов указывается последняя позиция в шаблоне (исключая последнюю букву) каждого из символов алфавита. Для всех символов, не вошедших в шаблон, пишем [math]m[/math]. Предположим, что у нас не совпал символ [math]c[/math] из текста на очередном шаге с символом из шаблона. Очевидно, что в таком случае мы можем сдвинуть шаблон до первого вхождения этого символа [math]c[/math] в шаблоне, т.к. совпадений других символов точно не может быть. Если в шаблоне такого символа нет, то можно можно сдвинуть весь шаблон полностью.

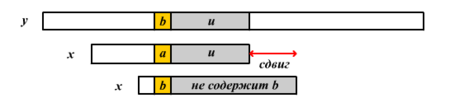
Если символ исходного текста [math]y[i + j][/math] встречается в шаблоне [math]x[/math], то происходит его выравнивание с его самым правым появлением в подстроке [math]x[0 .. m-2][/math].

Сдвиг плохого символа, символ [math]a[/math] входит в [math]x[/math].

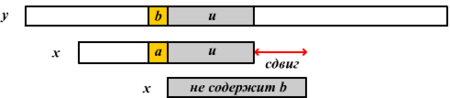
Если [math]y[i+j][/math] не встречается в шаблоне [math]x[/math], то ни одно вхождение [math]x[/math] в [math]y[/math] не может включать в себя [math]y[i+j][/math], и левый конец окна сравнения совмещен с символом непосредственно идущим после [math]y[i+j][/math], т.е. [math]y[i+j+1][/math].

Сдвиг плохого символа, символ [math]b[/math] не входит в [math]x[/math].

Обратите внимание, что сдвиг плохого символа может быть отрицательным.

Формальное определение

Таким образом для сдвига позиции начала сравнения алгоритм Бойера-Мура использует выбирает между двумя эвристическими функциями, называемыми эвристиками хорошего суффикса и плохого символа (иногда они называются эвристиками совпавшего суффикса и стоп-символа). Так как функции эвристические, то выбор между ними простой — ищется такое итоговое значение, чтобы мы не проверяли максимальное число позиций и при этом нашли все подстроки равные шаблону. Исходя из вышесказанных свойств этих функций можно брать значение равное максимуму между сдвигом хорошего суффикса и сдвига плохого символа.

Теперь определим две функции сдвигов более формально следующим образом:

Пусть значения функции сдвига хорошего суффикса хранятся в массиве [math]bmGs[/math] размером [math]m+1[/math].

Определим два условия:

• [math]Cs(i, s)[/math]: для каждого [math]k[/math] такого, что [math]i \lt k \lt m[/math] выполняется [math]s \geqslant k[/math] или [math]x[k-s]=x[k][/math]
• [math]Co(i, s)[/math]: если [math]s \lt i[/math], то выполняется [math]x[i-s] \neq x[i][/math]

Тогда для всех [math]i[/math] таких, что [math]0 \leqslant i \lt m[/math] выполняется [math]bmGs[i+1]=\min\{s \gt 0 : Cs(i, s)\ and\ Co(i, s)\}[/math]. А значение [math]bmGs[0][/math] определим, как длину периода шаблона [math]x[/math].

Для вычисления bmGs будем использовать массив [math]suff[/math], определенный так: для всех [math]i[/math] таких, что [math]1 \leqslant i \lt m[/math] выполняется [math]suff[i]=\max\{k : x[i-k+1 .. i]=x[m-k .. m-1]\}[/math]

Сдвиги плохих символов будем хранить в массиве [math]bmBc[/math] размером [math]\sigma[/math]. Для каждого символа [math]c[/math] из [math]\Sigma[/math]: [math]bmBc[c] = \begin{cases} \min\{i : 1 \leqslant i \lt m-1\ and\ x[m-1-i]=c\}, & \mbox{if } c \in x\\ m, & \mbox{otherwise} \end{cases}[/math]

Массивы [math]bmBc[/math] и [math]bmGs[/math] вычисляются за [math]O(m+\sigma)[/math] времени до основной фазы поиска и требуют, очевидно, [math]O(m+\sigma)[/math] памяти.

Псевдо-код

Константой [math]|\Sigma|=\sigma=ASIZE[/math] обозначим размер нашего алфавита.

Функция для вычисления таблицы сдвигов плохих символов. Она будет равна длине шаблона для всех символов, которые не встречаются в шаблоне, и порядковому номеру с конца для остальных (кроме последнего, для него тоже берется длина шаблона). Вычисляется прямо по определению за [math]O(m+\sigma)[/math]

  int[] preBmBc(string x, int m):
     int bmBc[ASIZE]
     // Значение по умолчанию = m
     for i = 0 .. ASIZE-1
        bmBc[i] = m
     for i = 0 .. m - 2
        bmBc[x[i]] = m - i - 1
     return bmBc

Функция для вычисления таблицы суффиксов. Она находит для каждой позиции в шаблоне [math]x[/math] максимальную длину суффикса [math]x[/math], который повторяется в строке и заканчивается в данной позиции.

Примеры:

Строка	Значение функции
abcabcabc	0, 0, 3, 0, 0, 6, 0, 0, 9
abcabcc	0, 0, 1, 0, 0, 1, 7

Также, очевидно, что значение функции для последнего элемента будет равно длине всей строки.

  int[] suffixes(string x, int m):
     int f = 0
     int suff[m]
     suff[m - 1] = m
     int g = m - 1
     for i = m - 2 .. 0
        if i > g and suff[i + m - 1 - f] < i - g
           suff[i] = suff[i + m - 1 - f]
        else
           if i < g
              g = i
           f = i
           while g >= 0 and x[g] == x[g + m - 1 - f]
              --g
           suff[i] = f - g
     return suff

Функция для вычисления сдвигов хороших суффиксов

  void preBmGs(string x, int m):
     int i, j, suff[XSIZE]
     int bmGs[]
     suff = suffixes(x, m)
     for i = 0 .. m - 1
        bmGs[i] = m
     j = 0
     for i = m - 1 .. 0
        if suff[i] == i + 1
           while j < m - 1 - i
              if bmGs[j] == m
                 bmGs[j] = m - 1 - i
              ++j
     for i = 0 .. m - 2
        bmGs[m - 1 - suff[i]] = m - 1 - i

Основная функция алгоритма Бойера-Мура

  void BM(string x, int m, string y, int n):
     int bmGs[m]
     int bmBc[ASIZE]

     //Предварительные вычисления
     bmGs = preBmGs(x, m)
     bmBc = preBmBc(x, m)
   
     //Поиск подстроки
     int j = 0
     while j <= n - m
        int i = m - 1
        while i >= 0 and x[i] == y[i + j]
           --i
        if i < 0
           OUTPUT(j) // Найдена подстрока в позиции j
           j += bmGs[0] //Очевидно, что можем сделать сдвиг на период, т.к. там явно не будет совпадений.
        else
           j += MAX(bmGs[i], bmBc[y[i + j]] - m + 1 + i)

Асимптотики

• Фаза предварительных вычислений требует [math]O(m + \sigma)[/math] времени и памяти
• В худшем случае поиск требует [math]O(m \cdot n)[/math] сравнений.
• В лучшем случае требует [math]O(n / m)[/math] сравнений.

где [math]n[/math] — длина исходного текста, [math]m[/math] — длина шаблона, [math]\sigma[/math] — размер алфавита.

В 1991 году Р.Коул доказал следующую теорему:

Теорема (Richard Cole):

В худшем случае требуется [math]O(3 \cdot n)[/math] сравнений в случае шаблона с периодом равным длине самого шаблона.

Доказательство:

[math]\triangleright[/math]

Доказательство [1]

[math]\triangleleft[/math]

Сравнение с другими алгоритмами

Достоинства

• Алгоритм Бойера-Мура на хороших данных очень быстр, а вероятность появления плохих данных крайне мала. Поэтому он оптимален в большинстве случаев, когда нет возможности провести предварительную обработку текста, в котором проводится поиск.
• На больших алфавитах (относительно длины шаблона) алгоритм чрезвычайно быстрый и требует намного меньше памяти относительно алгоритма Ахо-Корасик.
• Алгоритм проще большинства алгоритмов поиска (при некоторых реализациях объем кода сравним с наивным поиском)
• Позволяет добавить множество модификаций, таких как поиск подстроки, включающей любой символ (?) (но для реализации множества символов (*) не походит, т.к. длина шаблона должна быть известна заранее).

Недостатки

• Алгоритмы семейства Бойера-Мура не расширяются до приблизительного поиска, поиска любой строки из нескольких.
• На больших алфавитах (например, Юникод) может занимать много памяти. В таких случаях либо обходятся хэш-таблицами, либо дробят алфавит, рассматривая, например, 4-байтовый символ как пару двухбайтовых.
• На искусственно подобранных неудачных текстах (например, шаблон "abcabcabcabcabc") скорость алгоритма Бойера-Мура серьёзно снижается.

Варианты

Алгоритм Бойера — Мура — Хорспула

Этот алгоритм работает лучше Бойера-Мура на случайных текстах — для него оценка в среднем лучше. Алгоритм использует только сдвиги плохих символов, при этом за такой символ берётся символ из исходного текста, который соответствует последнему символу шаблона, независимо от того, где случилось несовпадение. Поскольку реальные поисковые образцы редко имеют равномерное распределение, алгоритм Бойера-Мура-Хорспула может дать как выигрыш, так и проигрыш по сравнению с стандартной реализацией.

Алгоритм Чжу — Такаоки

На коротких алфавитах сдвиги плохих символов не помогают уже на коротких суффиксах. Простейший способ улучшить работу алгоритма в таких условиях — вместо одного плохого символа строить таблицу для пары символов: несовпавшего и идущего перед ним. Такой алгоритм получил собственное имя: алгоритм Чжу — Такаоки. На предварительную обработку расходуется [math]O(m+\sigma^2)[/math] времени.

Ссылки

• Википедия — Алгоритм Бойера-Мура
• Википедия — Алгоритм Бойера-Мура-Хорспула
• Wikipedia — Boyer–Moore string search algorithm
• Boyer-Moore algorithm