Турбо-алгоритм Бойера-Мура

Турбо-алгоритм Бойера-Мура (англ. Turbo Boyer-Moore) является улучшением алгоритма Бойера-Мура. Турбо-алгоритм, разработанный группой учёных во главе с М.Крочемором, предлагает другой подход к коротким алфавитам и заодно решает вторую проблему — квадратичную сложность в худшем случае.

Алгоритм

Турбо-алгоритм Бойера-Мура не нуждается в дополнительном препроцессинге и требует только постоянную дополнительную память относительно оригинального алгоритма Бойера-Мура. Он состоит в запоминании сегмента текста, который соответствует суффиксу шаблона во время последней попытки (и только тогда, когда сдвиг хорошего суффикса был выполнен). Эта методика представляет два преимущества:

1. Можно перепрыгнуть через этот сегмент.
2. Она может позволить выполнение «турбо-сдвига».

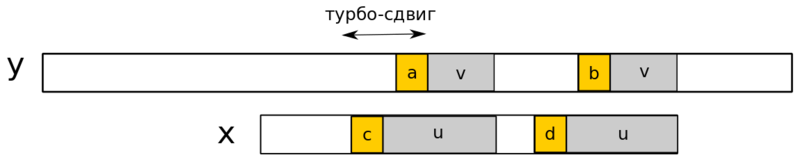
Турбо-сдвиг может произойти, если мы обнаружим, что суффикс образца, который сходится с текстом, короче, чем тот, который был запомнен ранее.

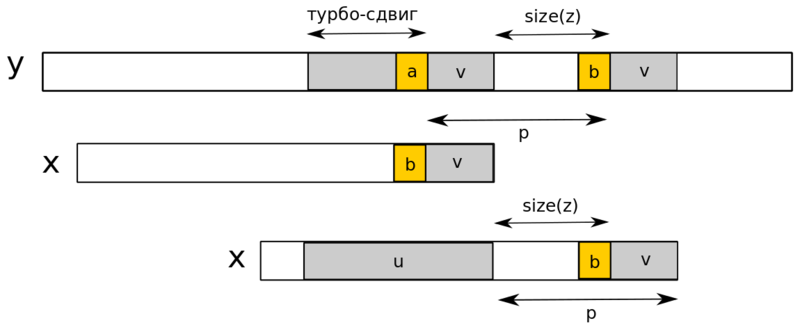
Пусть [math]u[/math] — запомненный сегмент, а [math]v[/math] — cуффикс, совпавший во время текущей попытки, такой что [math]uzv[/math] — суффикс [math]x[/math]. Тогда [math]av[/math] — суффикс [math]x[/math], два символа [math]a[/math] и [math]b[/math] встречаются на расстоянии [math]p[/math] в тексте, и суффикс [math]x[/math] длины [math]|uzv|[/math] имеет период длины [math]p[/math], а значит не может перекрыть оба появления символов [math]a[/math] и [math]b[/math] в тексте. Наименьший возможный сдвиг имеет длину [math]|u| - |v|[/math] (его мы и называем турбо-сдвигом).

Применение турбо-сдвига в случае |v| < |u|

При [math]|v| \lt |u|[/math], если сдвиг плохого символа больше, то совершаемый сдвиг будет больше либо равен [math]|u| - 1[/math]. В этом случае символы [math]c[/math] и [math]d[/math] различны, так как мы предположили, что предыдущий сдвиг был сдвигом хорошего суффикса. Тогда сдвиг больший, чем турбо-сдвиг, но меньший [math]|u| + 1[/math] совместит [math]c[/math] и [math]d[/math] с одним и тем же символом [math]v[/math]. Значит, если сдвиг плохого символа больше, то мы можем применить сдвиг больший либо равный [math]|u| + 1[/math].

Нельзя совместить символы [math]c \neq d[/math] с одним и тем же символом [math]v[/math].

Псевдокод

Стадия препроцессинга совпадает со стадией препроцессинга в алгоритме Бойера-Мура.

В сам алгоритм добавляется обработка турбо-сдвигов.

function TBM(char[] x, char[] y, int n, int m)
   int n = length(y)
   int m = length(x)
   int i = 0
   int u = 0
   int shift = m

   if (m == 0)
        return
        
   //Предварительные вычисления
   int bmBc[] = preBmBc(x, m)
   int bmGs[] = preBmGs(x, m)

   while (i <= n - m) 
       int j = m - 1
       while (j >= 0 and x[j] == y[i + j])
           --j
           if (u != 0 and j == m - 1 - shift) 
               j -= u
       if (j < 0) 
           print(i)
           shift = bm_gs[0]
           u = m - shift
       else 
           int v = m - 1 - j
           int turbo_shift = u - v
           int bc_shift = bm_bc[y[i + j]] - m + j + 1
           shift = max(turbo_shift, bc_shift, bm_gs[j + 1])
           if (shift == bm_gs[j + 1])
               u = min((m - shift), v)
           else 
               if (turbo_shift < bc_shift) 
                   shift = min(shift, (u + 1))
               u = 0
       i += shift

Асимптотика

Утверждение:

Фаза препроцессинга требует [math]O(m + \sigma)[/math] времени и памяти, где [math]\sigma[/math] — размер алфавита. Фаза поиска требует [math]O(n)[/math] времени. В худшем случае поиск требует [math]O(2n)[/math] сравнений.

[math]\triangleright[/math]

Разобьём поиск на стадии. Каждая стадия делится на две операции: сканирование и сдвиг. На этапе [math]k[/math] мы назовём [math]suf_k[/math] длину суффикса шаблона что совпадает с текстом. Этому предшествует символ, который не совпадает с соответствующим символом в тексте (в случае когда [math]suf_k[/math] не соответствует длине шаблона). Мы также назовём [math]shift_k[/math] длину сдвига сделанного на этапе [math]k[/math]. Рассмотрим три типа стадий в зависимости от характера сканирования и сдвига. Мы говорим, что сдвиг на стадии [math]k[/math] короткий, если [math]2shift_k \lt suf_k + 1[/math]. Тогда три типа сдвигов будут: Стадия с последующей стадией с прыжком. Стадия с длинным сдвигом, без последующей стадии с прыжком. Стадия с коротким сдвигом, без последующей стадии с прыжком. Идея доказательства состоит в амортизации сравнения со сдвигами. Определим стоимость [math]cost_k[/math] следующим образом: Если стадия [math]k[/math] имеет тип (1), [math]cost_k = 1[/math]. Если стадия [math]k[/math] имеет тип (2) или (3), стоимость [math]cost_k = suf_k + 1[/math]. В случае стадии типа (1), стоимость соответствует единственному сравнению несовпадающих символов. Другие сравнения, проведенные в течение той же стадии, являются стоимостью последующих этапов. Общее количество сравнений выполняемых алгоритмом это сумма стоимостей. Мы хотим доказать, что [math] \sum cost \lt 2 \sum shifts[/math]. Во второй [math] \sum [/math] длину последнего сдвига заменим [math]m[/math]. Даже с этим предположением, мы имеем [math] \sum shifts \lt |t|[/math], и если неравенство выполняется, тo [math] \sum cost \lt 2|t|[/math]. Для стадии типа (1), [math]cost_k = 1[/math] очевидным образом меньше, чем [math]2shift_k[/math], так как [math]shift_k \gt 0[/math]. Для стадии типа (2), [math]cost_k = suf_k + 1 \leqslant 2 shift_k[/math], по определению длинных сдвигов. Остается рассмотреть стадии типа (3). Так как в этой ситуации мы имеем [math]shift_k \lt suf_k[/math], единственный вариант, что обычный сдвиг применяется на стадии [math]k[/math]. Тогда мы запоминаем этот момент. На следующей стадии, [math]k + 1[/math], мы что-то запомнили, что приводит к возможному турбо-сдвигу. Ситуация на стадии [math]k + 1[/math], основная ситуация, когда турбо-сдвиг возможен. Прежде чем продолжить доказательство, мы сначала рассмотрим два случая и установим неравенства (по стоимости стадии [math]k[/math]), которые используем позже. Случай (а): [math]suf_k + shift_k \leqslant |p|[/math]. По определению турбо-сдвига, мы имеем [math]suf_k - suf_{k+1} \lt shift_{k + 1}[/math]. Таким образом, [math]cost_k = sufk + 1 \leqslant suf_{k+1} + shift_{k+1} + 1 \leqslant shift_k + shift_{k + 1}[/math]. Случай (б): [math]suf_k + shift_k \gt |p|[/math]. По определению турбо-сдвига, мы имеем [math]suf_{k+1} + shift_k + shift_{k + 1} \geqslant m[/math]. Тогда [math]cost_k \leqslant m \leqslant 2shift_k - 1 + shift_{k + 1}[/math].

[math]\triangleleft[/math]

См. также

• Алгоритм Бойера-Мура
• Алгоритм Райта
• Алгоритм Кнута-Морриса-Пратта
• Алгоритм Апостолико-Крочемора

Источники информации

• Википедия — Алгоритм Бойера-Мура
• Wikipedia — Boyer–Moore string search algorithm
• Turbo Boyer-Moore algorithm
• Турбо Боуер-Мур