Алгоритм Бойера-Мура

Алгоритм Бойера-Мура, разработанный двумя учеными — Бойером (Robert S. Boyer) и Муром (J. Strother Moore), считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска подстроки в строке. Важной особенностью алгоритма является то, что он выполняет сравнения в шаблоне справа налево в отличии от многих других алгоритмов.

Алгоритм Бойера-Мура считается наиболее эффективным алгоритмом поиска шаблонов в стандартных приложениях и командах, таких как Ctrl+F в браузерах и текстовых редакторах.

Алгоритм

Алгоритм сравнивает символы шаблона [math]y[/math] справа налево, начиная с самого правого, один за другим с символами исходной строки [math]x[/math]. В случае несовпадения какого-либо символа (или полного совпадения всего шаблона) он использует две предварительно вычисляемых функций, чтобы сдвинуть позицию для начала сравнения вправо.

Пусть [math]|y|=n[/math] и [math]|x|=m[/math].

Предположим, что в процессе сравнения возникает несовпадение между символом [math]x[i]=a[/math] шаблона и символом [math]y[i+j]=b[/math] исходного текста при проверке в позиции [math]j[/math]. Тогда [math]x[i+1 .. m-1]=y[i+j+1 .. j+m-1]=u[/math] и [math]x[i] \neq y[i+j][/math], т.е. [math]m - i - 1[/math] символов паттерна уже совпало.

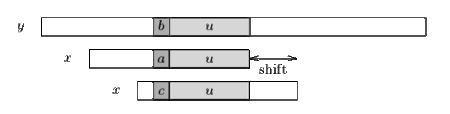
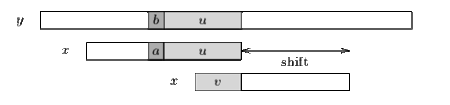
Операция сдвига хорошего суффикса состоит в выравнивании подстроки [math]u[/math] с её самым правым вхождением в [math]x[/math], идущим справа от символа, отличного от [math]x[i][/math].

Сдвиг хорошего суффикса, вся подстрока [math]u[/math] полностью встречается справа от символа [math]c[/math], отличного от символа [math]a[/math].

Если не существует такого сегмента, то смещение состоит в выравнивании самого длинного суффикса [math]v[/math] подстроки [math]y[i+j+1 .. j+m-1][/math] с соответствующим префиксом [math]x[/math].

Сдвиг хорошего суффикса, только суффикс подстроки [math]u[/math] повторно встречается в [math]x[/math].

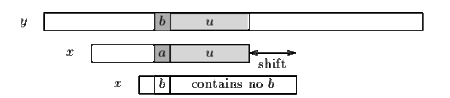
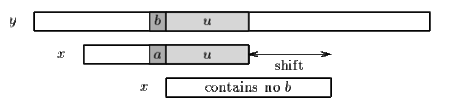
Операция сдвига плохого символа состоит в выравнивании символа исходного текста [math]у[i + j][/math] с его самым правым появлением в [math]x[0 .. m-2][/math].

Сдвиг плохого символа, символ [math]a[/math] входит в [math]x[/math].

Если [math]y[i+j][/math] не встречается в шаблоне x, то ни одно вхождение x в y не может включать в себя [math]y[i+j][/math], и левый конец окна сравнения совмещен с символом непосредственно идущим после [math]y[i+j][/math], т.е. [math]y[i+j+1][/math].

Сдвиг плохого символа, символ [math]b[/math] не входит в [math]x[/math].

Обратите внимание, что сдвиг плохого символа может быть отрицательным, таким образом для сдвига окна сравнения алгоритм Бойера-Мура использует значение, равное максимуму между сдвигом хорошего суффикса и сдвига плохого символа. Более формально две функции сдвигов определяются следующим образом:

Пусть значения функции сдвига хорошего суффикса хранятся в массиве [math]bmGs[/math] размером [math]m+1[/math].

Определим два условия:

• [math]Cs(i, s)[/math]: для каждого [math]k[/math] такого, что [math]i \lt k \lt m[/math] выполняется [math]s \geqslant k[/math] или [math]x[k-s]=x[k][/math]
• [math]Co(i, s)[/math]: если [math]s \lt i[/math], то выполняется [math]x[i-s] \neq x[i][/math]

Тогда для всех [math]i[/math] таких, что [math]0 \leqslant i \lt m[/math] выполняется [math]bmGs[i+1]=\min\{s \gt 0 : Cs(i, s)\ and\ Co(i, s)\}[/math]. А значение [math]bmGs[0][/math] определим, как длину периода шаблона [math]x[/math].

Для вычисления bmGs будем использовать массив [math]suff[/math], определенный так: для всех [math]i[/math] таких, что [math]1 \leqslant i \lt m[/math] выполняется [math]suff[i]=\max\{k : x[i-k+1 .. i]=x[m-k .. m-1]\}[/math]

Сдвиги плохих символов будем хранить в массиве [math]bmBc[/math] размером [math]\sigma[/math]. Для каждого символа [math]c[/math] из [math]\Sigma[/math]: [math]bmBc[c] = \begin{cases} \min\{i : 1 \leqslant i \lt m-1\ and\ x[m-1-i]=c\}, & \mbox{if } c \in x\\ m, & \mbox{otherwise} \end{cases}[/math]

Массивы [math]bmBc[/math] и [math]bmGs[/math] вычисляются за [math]O(m+\sigma)[/math] времени до основной фазы поиска и требуют, очевидно, [math]O(m+\sigma)[/math] памяти.

Псевдо-код

Константой [math]|\Sigma|=\sigma=ASIZE[/math] обозначим размер нашего алфавита.

Функция для вычисления таблицы сдвигов плохих символов. Она будет равна длине шаблона для всех символов, которые не встречаются в шаблоне, и порядковому номеру с конца для остальных (кроме последнего, для него тоже берется длина шаблона). Вычисляется прямо по определению за [math]O(m+\sigma)[/math]

  int[] preBmBc(string x, int m):
     int bmBc[ASIZE];
     // Значение по умолчанию = m
     for i = 0 .. ASIZE-1
        bmBc[i] = m;
     for i = 0 .. m - 2
        bmBc[x[i]] = m - i - 1;
     return bmBc;

Функция для вычисления таблицы суффиксов. Она находит для каждой позиции в шаблоне [math]x[/math] максимальную длину суффикса [math]x[/math], который повторяется в строке и заканчивается в данной позиции. Например, для строки "abcabcabc" таблица будет 0,0,3,0,0,6,0,0,9, а для строки "abcabcc" - 0,0,1,0,0,1,7. Также, очевидно, что значение функции для последнего элемента будет равно длине всей строки.

  int[] suffixes(string x, int m):
     int f;
     int suff[m];
     suff[m - 1] = m;
     int g = m - 1;
     for i = m - 2 .. 0
        if (i > g and suff[i + m - 1 - f] < i - g)
           suff[i] = suff[i + m - 1 - f];
        else
           if (i < g)
              g = i;
           f = i;
           while (g >= 0 and x[g] == x[g + m - 1 - f])
              --g;
           suff[i] = f - g;
     return suff;

Функция для вычисления сдвигов хороших суффиксов

  void preBmGs(string x, int m):
     int i, j, suff[XSIZE];
     int bmGs[]
     suff = suffixes(x, m);

     for (i = 0; i < m; ++i)
        bmGs[i] = m;
     j = 0;
     for i = m - 1 .. 0
        if (suff[i] == i + 1)
           while (j < m - 1 - i)
              if (bmGs[j] == m)
                 bmGs[j] = m - 1 - i;
              ++j
     for i = 0 .. m - 2
        bmGs[m - 1 - suff[i]] = m - 1 - i;

Основная функция алгоритма Бойера-Мура

  void BM(string x, int m, string y, int n):
     int bmGs[m];
     int bmBc[ASIZE];

     //Предварительные вычисления
     bmGs = preBmGs(x, m);
     bmBc = preBmBc(x, m);
   
     //Поиск подстроки
     int j = 0;
     while (j <= n - m)
        int i = m - 1;
        while (i >= 0 and x[i] == y[i + j])
           --i
        if (i < 0)
           OUTPUT(j); // Найдена подстрока в позиции j
           j += bmGs[0]; //Очевидно, что можем сделать сдвиг на период, т.к. там явно не будет совпадений.
        else
           j += MAX(bmGs[i], bmBc[y[i + j]] - m + 1 + i);

Асимптотики

• Фаза предварительных вычислений требует [math]O(m + \sigma)[/math] времени и памяти
• В худшем случае поиск требует [math]O(m \cdot n)[/math] сравнений.
• В лучшем случае требует [math]O(n / m)[/math] сравнений.

В 1991 году Р.Коул доказал следующую теорему:

Теорема (Richard Cole):

В худшем случае требуется [math]O(3 \cdot n)[/math] сравнений в случае шаблона с периодом равным длине самого шаблона.

Доказательство:

[math]\triangleright[/math]

Доказательство [1]

[math]\triangleleft[/math]

Сравнение с другими алгоритмами

Достоинства

• Алгоритм Бойера-Мура на хороших данных очень быстр, а вероятность появления плохих данных крайне мала. Поэтому он оптимален в большинстве случаев, когда нет возможности провести предварительную обработку текста, в котором проводится поиск.
• На больших алфавитах (относительно длины шаблона) алгоритм чрезвычайно быстрый и требует намного меньше памяти относительно алгоритма Ахо-Корасик.
• Алгоритм проще большинства алгоритмов поиска (при некоторых реализациях объем кода сравним с наивным поиском)
• Позволяет добавить множество модификаций, таких как поиск подстроки, включающей любой символ (?) (но для реализации множества символов (*) не походит, т.к. длина шаблона должна быть известна заранее).

Недостатки

• Алгоритмы семейства Бойера-Мура не расширяются до приблизительного поиска, поиска любой строки из нескольких.
• На больших алфавитах (например, Юникод) может занимать много памяти. В таких случаях либо обходятся хэш-таблицами, либо дробят алфавит, рассматривая, например, 4-байтовый символ как пару двухбайтовых.
• На искусственно подобранных неудачных текстах (например, шаблон "abcabcabcabcabc") скорость алгоритма Бойера-Мура серьёзно снижается.

Ссылки

• Википедия:Алгоритм Бойера-Мура
• Википедия:Алгоритм Бойера-Мура-Хорспула
• Wikipedia:Boyer–Moore string search algorithm
• Boyer-Moore algorithm