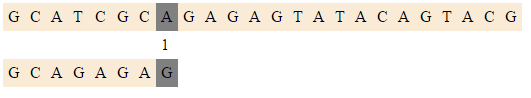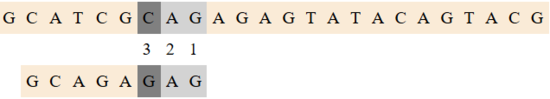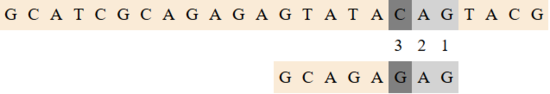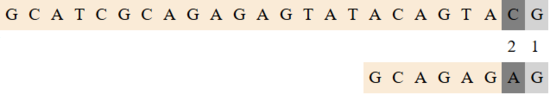Турбо-алгоритм Бойера-Мура

Материал из Викиконспекты
Перейти к: навигация, поиск

Турбо-алгоритм Бойера-Мура (англ. Turbo Boyer-Moore) является улучшением алгоритма Бойера-Мура. Турбо-алгоритм, разработанный группой учёных во главе с М.Крочемором, предлагает другой подход к коротким алфавитам и заодно решает вторую проблему — квадратичную сложность в худшем случае.

Алгоритм

Турбо-алгоритм Бойера-Мура не нуждается в дополнительном препроцессинге и требует только постоянную дополнительную память относительно оригинального алгоритма Бойера-Мура. Он состоит в запоминании сегмента текста, который соответствует суффиксу шаблона во время последней попытки (и только тогда, когда сдвиг хорошего суффикса был выполнен). Эта методика представляет два преимущества:

  1. Можно перепрыгнуть через этот сегмент.
  2. Она может позволить выполнение «турбо-сдвига».

Турбо-сдвиг может произойти, если мы обнаружим, что суффикс образца, который сходится с текстом, короче, чем тот, который был запомнен ранее.

Определение турбо-сдвига

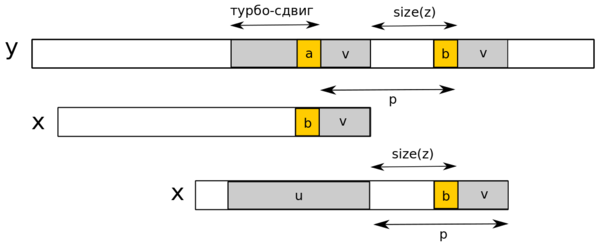
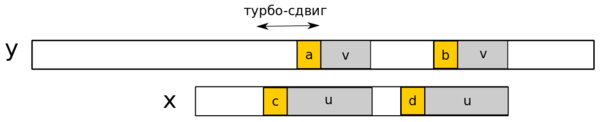
Пусть [math]u[/math] — запомненный сегмент, а [math]v[/math] — cуффикс, совпавший во время текущей попытки, такой что [math]uzv[/math] — суффикс [math]x[/math]. Тогда [math]av[/math] — суффикс [math]x[/math], два символа [math]a[/math] и [math]b[/math] встречаются на расстоянии [math]p[/math] в тексте, и суффикс [math]x[/math] длины [math]|uzv|[/math] имеет период длины [math]p[/math], а значит не может перекрыть оба появления символов [math]a[/math] и [math]b[/math] в тексте. Наименьший возможный сдвиг имеет длину [math]|u| - |v|[/math] (его мы и называем турбо-сдвигом).
Tbm1.png

Применение турбо-сдвига в случае |v| < |u|

При [math]|v| \lt |u|[/math], если длина сдвига плохого символа больше, чем длина сдвига хорошего суффикса и длины турбо-сдвига, то длина фактического сдвига должна быть больше или равна [math]|u| + 1[/math]. Действительно, в этом случае два символа [math]c[/math] и [math]d[/math] различны, так как мы предположили, что предыдущий сдвиг был сдвигом хороший суффикса. Тогда сдвиг больший, чем турбо-сдвиг, но меньший, чем [math]|u| +1[/math] будет выравнивать [math]c[/math] и [math]d[/math] с таким же символом в [math]v[/math], в этом случае длина фактического сдвига должна быть по крайней мере равен [math]|u| +1[/math].

Tbm2.png

Нельзя совместить символы [math]c \neq d[/math] с одним и тем же символом [math]v[/math].

Описание алгоритма

В алгоритм Бойера-Мура дополнительно добавится запоминание длины [math]|u|[/math] сегмента текста, который соответствует суффиксу шаблона во время последней попытки, который мы не будем лишний раз рассматривать при сравнении суффиксов двух подстрок, а также запоминании размера сдвига [math]shift[/math], который мы совершили. Вычислять его будем следующим образом:

  • Если текущем шаге у нас подстрока совпала с шаблоном [math]x[/math], то [math]shift = bmGs[0][/math] ([math]bmGs[0][/math] равен периоду шаблона [math]x[/math]), [math]|u| = m - shift[/math].
  • Иначе возможны два случая:
    • Если сдвиг хорошего суффикса не меньше турбо-сдвига и сдвига плохого символа, тогда [math]shift = bmGs[j+1][/math], [math]|u| = min(m - shift, |v|)[/math] ([math]v[/math] текущая подстрока).
    • В противном случае, [math]|u| = 0)[/math], [math]shift = max(turboShift, bCShift)[/math]([math]turboShift[/math] длина турбо-сдвига, [math]bCShift[/math] длина сдвига плохого символа), если турбо-сдвиг меньше сдвига плохого символа, то [math]shift[/math] должен быть не больше [math]|u_0| + 1[/math] ([math]u_0[/math] сегмент текста, рассматриваемый на прошлом шаге).

Псевдокод

Стадия препроцессинга совпадает со стадией препроцессинга в алгоритме Бойера-Мура, функция вычислений сдвигов плохих символов и функция вычисления хороших суффиксов не меняются, меняется только сам алгоритм, в него добавляется обработка турбо-сдвигов. 

function TBM(char[] x, char[] y, int n, int m): List<int>
   int i = 0
   int u = 0
   int shift = m
   List<int> answer;

   if (m == 0)
        return
        
   //Предварительные вычисления
   int bmBc[] = preBmBc(x, m)
   int bmGs[] = preBmGs(x, m)

   while (i <= n - m) 
       int j = m - 1
       while (j >= 0 and x[j] == y[i + j])
           --j
           if (u != 0 and j == m - 1 - shift) 
               j -= u
       if (j < 0) 
           answer.add(i)
           shift = bmGs[0]
           u = m - shift
       else 
           int v = m - 1 - j
           int turboShift = u - v
           int bCShift = bmBc[y[i + j]] - m + j + 1
           shift = max(turboShift, bCShift, bmGs[j + 1])
           if (shift == bmGs[j + 1])
               u = min((m - shift), v)
           else 
               if (turboShift < bcShift) 
                   shift = min(shift, (u + 1))
               u = 0
       i += shift
   return answer

Асимптотика

Утверждение:
Фаза препроцессинга требует [math]O(m + \sigma)[/math] времени и памяти, где [math]\sigma[/math] — размер алфавита, [math]m[/math] — длина шаблона.
[math]\triangleright[/math]
Стадия препроцессинга совпадает со стадией препроцессинга в алгоритме Бойера-Мура, поэтому рассмотрим только стадию поиска.
[math]\triangleleft[/math]
Утверждение:
Фаза поиска требует [math]O(n)[/math] времени, где [math]n[/math] — длина строки, в которой выполняется поиск.
Утверждение:
В худшем случае поиск требует [math]O(2n)[/math] сравнений.
[math]\triangleright[/math]

Разобьём поиск на шаги, каждый из которых будет состоять из двух операций: сканирования и сдвига. На шаге [math]k[/math] мы будем называть [math]suf_k[/math] длину суффикса шаблона, что совпадает с текстом, перед суффиксом шаблона будет символ, который не совпадает с соответствующим символом в тексте (в случае когда [math]suf_k[/math] не соответствует длине шаблона). Мы также будем называть [math]shift_k[/math] длину сдвига, сделанного на шаге [math]k[/math].

Рассмотрим три типа шагов в зависимости от характера сканирования и сдвига. Мы говорим, что сдвиг на шаге [math]k[/math] короткий, если [math]2shift_k \lt suf_k + 1[/math]. Тогда эти три типа будут:

  1. Шаг с последующим шагом с прыжком.
  2. Шаг с длинным сдвигом, без последующего шага с прыжком.
  3. Шаг с коротким сдвигом, без последующего шага с прыжком.

Идея доказательства состоит в амортизации стоимости сравнения со сдвигами. Определим стоимость шага [math]cost_k[/math] следующим образом:

  • Если шаг [math]k[/math] имеет тип (1), [math]cost_k = 1[/math].
  • Если шаг [math]k[/math] имеет тип (2) или (3), стоимость [math]cost_k = suf_k + 1[/math].

Общее количество сравнений выполняемых алгоритмом это сумма стоимостей шагов. Мы хотим доказать, что [math] \sum cost \lt 2 \sum shifts[/math]. Во второй [math] \sum [/math] длину последнего сдвига заменим [math]m[/math]. В случае шага типа (1), стоимость соответствует единственному сравнению несовпадающих символов. Другие сравнения, проведенные в течение того же шага, являются стоимостью последующих шагов.

Рассмотрим каждый тип шага:

  1. [math]cost_k = 1[/math] очевидным образом меньше, чем [math]2shift_k[/math], так как [math]shift_k \gt 0[/math].
  2. [math]cost_k = suf_k + 1 \leqslant 2 shift_k[/math], по определению длинных сдвигов.
  3. Так как в этой ситуации мы имеем [math]shift_k \lt suf_k[/math], единственный вариант — обычный сдвиг применяется на шаге [math]k[/math]. Тогда мы должны это запомнить. На следующем шаге, [math]k + 1[/math], мы что-то запомнили, что приводит к возможному турбо-сдвигу. Ситуация на шаге [math]k + 1[/math], основная ситуация, когда турбо-сдвиг возможен. Прежде чем продолжить доказательство, мы сначала рассмотрим два случая и установим неравенства (по стоимости шага [math]k[/math]), которые используем позже.
    • Случай (а): [math]suf_k + shift_k \leqslant |p|[/math]. По определению турбо-сдвига, мы имеем [math]suf_k - suf_{k+1} \lt shift_{k + 1}[/math]. Таким образом, [math]cost_k = sufk + 1 \leqslant suf_{k+1} + shift_{k+1} + 1 \leqslant shift_k + shift_{k + 1}[/math].
    • Случай (б): [math]suf_k + shift_k \gt |p|[/math]. По определению турбо-сдвига, мы имеем [math]suf_{k+1} + shift_k + shift_{k + 1} \geqslant m[/math]. Тогда [math]cost_k \leqslant m \leqslant 2shift_k - 1 + shift_{k + 1}[/math].
Можно считать, что на шаге [math]k + 1[/math] случай (б) имеет место, потому что это дает нам верхнюю границу [math]cost_k[/math] (это верно, если [math]shift_k \geqslant 2[/math], случай [math]shift_k = 1[/math] можно обрабатывать напрямую). Если шаг [math]k + 1[/math] типа (1), то [math]cost_{k + 1} = 1[/math], а затем [math]cost_k + cost_{k+1} \leqslant 2shift_k + shift_{k+1}[/math], что даже лучше, чем ожидалось. Если на шаге [math]k + 1[/math] мы имеем [math]suf_{k + 1} \leqslant shift_{k + 1}[/math], то мы получим то, что ожидалось: [math]cost_k + cost_{k + 1} \leqslant 2shift_k + 2shift_{k + 1}[/math]. Последняя ситуация для рассмотрения, когда на шаге [math]k + 1[/math] мы имеем [math]suf_{k + 1} \gt shift_{k + 1}[/math]. Это означает, что, как уже упоминалось ранее, обычный сдвиг применяется на шаге [math]k + 1[/math]. Таким образом, приведенный выше анализ также применяется на шаге [math]k + 1[/math], и, так как только случай (а) может произойти тогда мы получаем [math]cost_{k + 1} \leqslant shift_{k + 1} + shift_{k + 2}[/math]. Мы, наконец, получаем [math]cost_k + cost_{k + 1} \leqslant 2shift_k + 2shift_{k + 1} + shift_{k + 2}[/math].

Покажем правильность шагов по индукции: если все шаги [math]k[/math] до [math]k + j[/math] таковы, что [math]suf_k \gt shift_k,... , suf_{k + j} \gt shift_{k + j}[/math], то [math]cost_k + ... + cost_{k + j} \leqslant 2shift_k + ... + 2shift_{k + j} + shift_{k + j + 1}[/math].
Пусть [math]k'[/math] первый этап после этапа [math]k[/math] такой, что [math]suf_{k'} \leqslant shift_{k'}[/math]. Целое число [math]k'[/math] существует потому, что иначе получим бесконечную последовательность сдвигов с уменьшающейся длиной. После этого мы получим [math]cost_k + ... + cost_{k'} \leqslant 2shift_k + ... + 2shift_{k'}[/math].

Это показывает нам, что [math] \sum cost_k \leqslant 2 \sum shift_k[/math], что и требовалось.
[math]\triangleleft[/math]

Пример работы

Пусть нам дана строка [math]y = GCATCGCAGAGAGTATACAGTACG[/math] и образец [math]x=GCAGAGAG[/math]

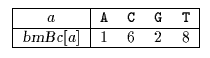
Построим массив [math]bmBc[/math]:

RaitaPre.png

Рассмотрим шаги алгоритма:

Изображение [math](j, bmBc[y[j]])[/math] Описание
Raita1.png [math](7, 1)[/math] Делаем сравнение последних символов, оно неудачно, сдвигаемся на [math]bmGs[7] = bmBc[A]-8+8 = 1[/math].
Tbme2.PNG [math](8, 2)[/math] Последние два символа совпали, сдвигаемся на [math]bmGs[5] = bmBc[C] - 8 + 6 = 4[/math].
Tbme3.PNG [math](12, 2)[/math] Все символы совпали, Продолжим работу (для примера, в обычном варианте на этом этапе мы можем выйти, если требуется найти только одно вхождение) и сдвинемся на [math]bmGs[0] = 7[/math].
Tbme4.PNG [math](19, 2)[/math] Последние два символа совпали, сдвигаемся на [math]bmGs[5] = bmBc[C] - 8 + 6 = 4[/math].
Tbme5.PNG [math](23, 1)[/math] Последние символы совпали, сравниваем предпоследние, сдвигаемся. Строка закончилась, выходим.

В итоге, чтобы найти одно вхождение образца длиной [math]m = 8[/math] в образце длиной [math]n = 24[/math] нам понадобилось [math]15[/math] сравнений символов

См. также

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Турбо-алгоритм_Бойера-Мура&oldid=53577»