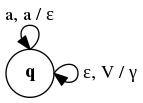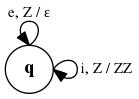Совпадение множества языков МП-автоматов и контекстно-свободных языков

Материал из Викиконспекты
Перейти к: навигация, поиск
НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.

Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.

Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.

Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.

Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Построение МП-автомата по заданной КС-грамматике

Теорема:
Класс контекстно-свободных языков [math](\mathrm{CFG})[/math] является подмножеством класса языков, задаваемых автоматами с магазинной памятью [math](\mathrm{PDA})[/math], то есть по любой КС-грамматике можно построить МП-автомат, задающий тот же язык, что и исходная грамматика.
Доказательство:
[math]\triangleright[/math]

Пусть дана КС-грамматика [math]\Gamma =\langle \Sigma, N, S, P\rangle[/math]. Поскольку классы языков, допускаемых МП-автоматами по допускающему состоянию и по пустому стеку, совпадают, достаточно построить автомат с допуском по пустому стеку.

Построим автомат из одного состояния [math]q[/math] с входным алфавитом [math]\Sigma[/math], стековым алфавитом [math]N \cup \Sigma[/math], маркером дна [math]S[/math] и функцией перехода [math]\delta[/math], определённой ниже. Формально [math]A = \langle \Sigma, N \cup \Sigma, \{q\}, q, S, \delta \rangle[/math], где [math]\delta[/math] задаётся следующим образом:

Добавим такие переходы для каждого терминала [math]a[/math] и правила вывода [math]V \rightarrow \gamma[/math]
  • для каждого правила вывода [math]V \rightarrow \gamma \in P[/math] определим [math]\delta(q, \varepsilon, V) = \{(q, \gamma)\}[/math];
  • для каждого терминала [math]a[/math] определим [math] \delta(q, a, a) = \{(q, \varepsilon)\} [/math].

Покажем, что язык, допускаемый автоматом [math]A[/math], совпадает с языком грамматики [math]\Gamma[/math], то есть что [math]S \Rightarrow^* w \iff (q, w, S) \vdash^* (q, \varepsilon, \varepsilon)[/math]:

Пусть [math]S \Rightarrow^* w[/math].
Рассмотрим левосторонний вывод [math]S = \gamma_0 \Rightarrow \gamma_1 \Rightarrow ... \Rightarrow \gamma_n=w[/math]. Обозначим как [math]v_i[/math] наибольший префикс [math]\gamma_i[/math], состоящий только из терминалов, а [math]\alpha_i[/math] — остаток [math]\gamma_i[/math], то есть [math]\gamma_i = v_i\alpha_i[/math], причём [math]v_i \in \Sigma^*[/math], а [math]\alpha_i[/math] начинается с нетерминала (либо пустая). С помощью индукции по [math]i[/math] докажем, что [math](q, w, S) \vdash^* (q, x_i, \alpha_i)[/math] для [math]i \leq n[/math], где [math]x_i[/math] — то, что остаётся после чтения [math]v_i[/math], то есть [math]v_ix_i = w[/math]. Иными словами, переходя по автомату по символам [math]v_i[/math], можно оставить на стеке [math]\alpha_i[/math].
  • База:
    Пусть [math]i = 0[/math].
    В этом случае [math]\gamma_0 = S[/math], поэтому [math]v_0 = \varepsilon, \alpha_0 = S, x_i = w[/math]. Очевидно, [math](q, w, S) \vdash^* (q, w, S)[/math].
  • Индукционный переход:
    Пусть [math](q, w, S) \vdash^* (q, x_i, \alpha_i)[/math] для [math]i \lt n[/math]. [math]\alpha_i[/math] по определению начинается с какого-то нетерминала [math]V[/math] (если [math]\alpha_i = \varepsilon[/math], то получена [math]\gamma_n[/math], а мы предположили, что [math]i \lt n[/math]), то есть [math]\alpha_i = Vq_i[/math] Поскольку мы рассматриваем левосторонний вывод, то переход [math]\gamma_i \Rightarrow \gamma_{i + 1}[/math] включает замену нетерминала [math]V[/math] на какую-то цепочку [math]\beta[/math] по правилу [math]V \rightarrow \beta[/math]. Так как [math]\gamma_i = v_i \alpha_i = v_i V q_i[/math], то [math]\gamma_{i + 1} = v_i \beta q_i = v_{i + 1} \alpha_{i + 1}[/math]. В автомате [math]A[/math] по построению присутствует правило перехода [math]\delta(q, \varepsilon, V) = \{(q, \beta)\}[/math], поэтому [math]\alpha_i[/math] на стеке можно заменить на [math]\beta q_i[/math]. Заметим, что [math]\beta q_i[/math] представляет собой конкатенацию нескольких терминалов из [math]w[/math] и [math]\alpha_{i + 1}[/math]. Считывая очередные символы строки [math]w[/math], будем переходить по автомату, убирая терминалы со стека, пока не встретим нетерминал. Таким образом, на стеке окажется [math]\alpha_{i+1}[/math]. Получили, что [math](q, x_i, \alpha_i) \vdash^* (q, x_{i + 1}, \alpha_{i + 1})[/math], а значит, [math](q, w, S) \vdash^* (q, x_{i + 1}, \alpha_{i + 1})[/math]. Индукционный переход доказан.
Заметим, что [math]\alpha_n = \varepsilon, v_n = w, x_n = \varepsilon[/math], поэтому [math](q, w, S) \vdash^* (q, \varepsilon, \varepsilon)[/math].
Пусть [math](q, w, S) \vdash^* (q, \varepsilon, \varepsilon)[/math].
Воспользуемся индукцией по числу переходов в автомате и докажем для любой строки [math]x[/math] и нетерминала [math]M \in N[/math], что если [math](q, x, M) \vdash^* (q, \varepsilon, \varepsilon)[/math], то [math]M \Rightarrow^* x[/math].
  • База:
    Пусть в автомате один переход.
    Если [math](q, x, M) \vdash^* (q, \varepsilon, \varepsilon)[/math], то [math]x = \varepsilon[/math] и в грамматике присутствует правило [math]M \rightarrow \varepsilon[/math], по которому выводится [math]\varepsilon = x[/math].
  • Индукционный переход:
    Предположим, что автомат [math]A[/math] совершает [math]n[/math] шагов ([math]n \gt 1[/math]). Изначально на вершине стеке находится [math]M[/math], поэтому первый переход совершается по какому-то правилу из первого пункта построения [math]\delta[/math], и на стеке оказывается последовательность из терминалов и нетерминалов [math]Y_1 Y_2 \ldots Y_k[/math]. В процессе следующих [math]n - 1[/math] переходов автомат прочитает строку [math]x[/math] и поочерёдно вытолкнет со стека [math]Y_1 Y_2 \ldots Y_k[/math]. Разобьём [math]w[/math] на подстроки [math]x_1 x_2 \ldots x_k[/math], где [math]x_1[/math] — порция входа, прочитанная до выталкивания [math]Y_1[/math] со стека, [math]x_2[/math] — следующая порция входа, прочитанная до выталкивания [math]Y_2[/math] со стека и так далее. Формально можно заключить, что [math](q, x_i x_{i + 1} \ldots x_k, Y_i) \vdash^* (q, x_{i + 1} \ldots x_k, \varepsilon)[/math], причём менее чем за [math]n[/math] шагов. Если [math]Y_i[/math] — нетерминал, то по индукционному предположению имеем, что [math]Y_i \Rightarrow^* x_i[/math]. Если же [math]Y_i[/math] — терминал, то должен совершаться только один переход, в котором проверяется совпадение [math]x_i[/math] и [math]Y_i[/math]. Значит, [math]Y_i \Rightarrow^* x_i[/math] за 0 шагов.
    Таким образом, получаем, что [math]M \Rightarrow Y_1 Y_2 \ldots Y_k \Rightarrow^* x_1 x_2 \ldots x_k = x[/math].
Подставляя [math]w[/math] вместо [math]x[/math] и [math]S[/math] вместо [math]M[/math], получаем, что [math]S \Rightarrow^* w. [/math]
[math]\triangleleft[/math]

Пример

Поскольку доказательство теоремы конструктивно, то используя правила перехода, описанные в ней, можно преобразовать любую КС-грамматику в МП-автомат. Рассмотрим грамматику слов над алфавитом [math]\{0, 1\}[/math], в которых одинаковое количество нулей и единиц:

[math] S \rightarrow 0S1 [/math]
[math] S \rightarrow 1S0 [/math]
[math] S \rightarrow \varepsilon [/math]

Множеством терминалов является [math]\Sigma = \{0, 1\}[/math], а нетерминалов — [math]N = \{S\}[/math]. Таким образом, стековый алфавит состоит из [math]0, 1, S[/math]. Функция переходов [math]\delta[/math] определена следующим образом:

[math]\delta(q, \varepsilon, S) = \{(q, 0S1), (q, 1S0), (q, \varepsilon)\}[/math] (в соответствии с первым пунктом построения [math]\delta[/math])
[math] \delta(q, 0, 0)= \{(q, \varepsilon)\}[/math]; [math] \delta(q, 1, 1)= \{(q, \varepsilon)\}[/math] (в соответствии со вторым пунктом построения [math]\delta[/math])

Получившийся автомат:

Example1.png

Построение КС-грамматики по МП-автомату

Теорема:
Класс языков, задаваемых автоматами с магазинной памятью [math](\mathrm{PDA})[/math], является подмножеством класса контекстно-свободных языков [math](\mathrm{CFG})[/math], то есть по любому МП-автомату можно построить КС-грамматику, задающую тот же язык, что и допускаемый автоматом.
Доказательство:
[math]\triangleright[/math]

Пусть дан МП-автомат с допуском по пустому стеку [math]A = \langle \Sigma, \Pi, Q, q_0 \in Q, z_0, \delta \rangle[/math]. Как отмечалось ранее, предположение о допуске по пустому стеку не умаляет общности. Построим эквивалентную ему КС-грамматику [math]\Gamma = \langle \Sigma, N, S, P \rangle[/math]. В качестве нетерминалов будем использовать конструкции вида [math][pXq][/math] (где [math] p, q \in Q[/math], [math]X \in \Pi[/math]), которая неформально означает, что в процессе изменения состояния автомата от [math]p[/math] до [math]q[/math] символ [math]X[/math] удаляется с вершины стека, не затрагивая то, что находится ниже. Также введём стартовый нетерминал [math]S[/math]. Таким образом, [math]N = Q \times \Pi \times Q \cup S[/math].

Правила вывода [math]P[/math] построим следующим образом:

  • для каждого состояния [math]p \in Q[/math] добавим правило [math]S \rightarrow [q_0 z_0 p][/math];
  • для каждого перехода [math](r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)[/math] сделаем следующее: для всех упорядоченных списков состояний [math][r_1, r_2 \ldots r_k] \in Q^k[/math] добавим правило [math][p X r_k] \rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k][/math], если [math]k \gt 0[/math], и [math][p X r_0] \rightarrow a[/math], если [math]k = 0[/math].

Нетерминал [math][pXq][/math] должен выводить только те строки [math]w[/math], которые переводят автомат из состояния [math](p, X)[/math] в [math](q, \varepsilon)[/math]. Формально это можно записать следующим образом: [math][pXq] \Rightarrow^* w \iff (p, w, X) \vdash^* (q, \varepsilon, \varepsilon)[/math]. Докажем это утверждение:

Пусть [math](p, w, X) \vdash^* (q, \varepsilon, \varepsilon)[/math].
Докажем, что [math][pXq] \Rightarrow^* w[/math], используя индукцию по числу переходов в автомате.
  • База:
    Пусть выполняется только один переход.
    Тогда длина [math]w[/math] не больше единицы и [math](q, \varepsilon) \in \delta(p, w, X)[/math], поэтому правило [math][pXq] \rightarrow w[/math] по построению должно присутствовать в [math]P[/math].
  • Индукционный переход:
    Предположим, что [math](p, w, X) \vdash^* (q, \varepsilon, \varepsilon)[/math] за [math]n \gt 1[/math] шагов. Первый переход имеет вид [math](p, w, X) \vdash (r_0, x, \gamma_1 \gamma_2 \ldots \gamma_k) \vdash^* (q, \varepsilon, \varepsilon)[/math], где [math]w = ax[/math] ([math]a[/math] — символ из [math]\Sigma[/math] или [math]\varepsilon[/math]). Значит, [math](r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)[/math]. По построению в грамматике должно присутствовать правило [math][p X r_k] \rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k][/math] для любой последовательности состояний [math][r_1, \ldots r_k][/math]. Пусть [math]x = w_1 w_2 \ldots w_k[/math], где [math]w_i[/math] — входная цепочка, которая прочитывается до удаления [math]\gamma_i[/math] со стека, то есть найдётся такая последовательность состояний [math][r_1, \ldots r_k][/math], что [math](r_{i - 1}, w_i, \gamma_i) \vdash^* (r_i, \varepsilon, \varepsilon)[/math], причём заканчивается всё в [math]q = r_k[/math]. Заметим, что все эти выводы содержат менее [math]n[/math] переходов, а значит, по индукционному предположению [math][r_{i - 1} \gamma_i r_i] \Rightarrow^* w_i[/math] для всех [math]i[/math].
    Собирая вышесказанное, получаем [math][p X r_k] \Rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k] \Rightarrow^* a w_1 w_2 \ldots w_k = w[/math]. Так как [math]r_k = q[/math], то [math][pXq] \Rightarrow^* w[/math], тем самым индукционный переход доказан.
Пусть [math][pXq] \Rightarrow^* w[/math].
Докажем, что [math](p, w, X) \vdash^* (q, \varepsilon, \varepsilon)[/math], используя индукцию по числу шагов в порождении.
  • База:
    Пусть [math][pXq] \Rightarrow^* w[/math] за один шаг.
    Тогда в [math]\Gamma[/math] должно быть правило вывода [math][pXq] \rightarrow w[/math], а значит, в автомате должен быть переход [math](q, \varepsilon) \in \delta(p, w, X)[/math] и [math]w[/math] не может иметь длину больше единицы. Таким образом, [math](p, w, X) \vdash^* (q, \varepsilon, \varepsilon)[/math].
  • Индукционный переход:
    Предположим, что [math][pXq] \Rightarrow^* w [/math] за [math]n \gt 1[/math] шагов. По построению вывод должен иметь вид [math][p X r_k] \Rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k] \Rightarrow^* w[/math], где [math]r_k = q[/math] и [math](r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)[/math]. Вновь представим [math]w[/math] в виде [math]w = a w_1 w_2 \ldots w_k[/math] так, что [math][r_{i - 1} \gamma_i r_i] \Rightarrow^* w_i[/math]. Так как все эти выводы содержат менее [math]n[/math] шагов, то по индукционному предположению для всех [math]i[/math] выполнено [math](r_{i - 1}, w_i, \gamma_i) \vdash^* (r_i, \varepsilon, \varepsilon)[/math]. Собирая всё вместе, получаем [math](r_0, w_1 w_2 \ldots w_k, \gamma_1 \gamma_2 \ldots \gamma_k) \vdash^* (r_1, w_2 w_3 \ldots w_k, \gamma_2 \gamma_3 \ldots \gamma_k) \vdash^* \ldots \vdash^* (r_k, \varepsilon, \varepsilon)[/math]. Так как [math](r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)[/math] и [math]r_k = q[/math], то в итоге [math](p, w, X) \vdash^* (q, \varepsilon, \varepsilon)[/math].
Таким образом, мы доказали, что [math][pXq] \Rightarrow^* w \iff (p, w, X) \vdash^* (q, \varepsilon, \varepsilon)[/math]. Заметим, что [math]S \Rightarrow^* w[/math] тогда и только тогда, когда найдётся [math]p[/math], что [math][q_0 z_0 p] \Rightarrow^* w[/math]. По доказанному выше это равносильно тому, что [math](q_0, w, z_0) \vdash^* (p, \varepsilon, \varepsilon)[/math], то есть что [math]A[/math] допускает [math]w[/math] по пустому стеку. Суммируя всё вышесказанное, получаем, что построенная грамматика [math]\Gamma[/math] порождает слово [math]w[/math] тогда и только тогда, когда оно допускается автоматом [math]A[/math].
[math]\triangleleft[/math]

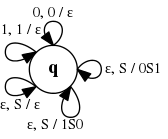
Пример

Пусть у нас имеется МП-автомат [math]A = \langle \{i,e\}, \{Z\}, \{q\}, q, Z, \delta \rangle[/math], функция [math]\delta[/math] задана следующим образом:

[math]\delta(q, i, Z) = \{(q, ZZ)\}[/math]
[math]\delta(q, e, Z) = \{(q, \varepsilon)\}[/math]

Example2.png

Так как стековый алфавит [math]A[/math] содержит лишь один символ и одно состояние, то в построенной грамматике будет лишь 2 нетерминала:

  • [math]S[/math] — стартовый нетерминал.
  • [math][qZq][/math] — единственная тройка, которую можно собрать из состояний автомата и символов стекового алфавита.

Также грамматика имеет следующие правила вывода:

  • Единственной продукцией для [math]S[/math] является [math]S \rightarrow [qZq][/math]. Но если бы у автомата было [math]n[/math] состояний, то тут бы имелось и [math]n[/math] продукций.
  • Из того факта, что [math]\delta(q, i, Z)[/math] содержит [math](q, ZZ)[/math], получаем правило вывода [math][qZq] \rightarrow i[qZq][qZq][/math]. Если бы у автомата было [math]n[/math] состояний, то такой переход порождал бы [math]n^2[/math] продукций.
  • Из [math]\delta(q,e,Z)=\{(q,\varepsilon)\}[/math] получаем правило вывода [math][qZq] \rightarrow e[/math]

Для удобства тройку [math][qZq][/math] можно заменить символом [math]A[/math], в таком случае правила вывода в грамматике будут следующие:

[math]S \rightarrow A[/math]
[math]A \rightarrow iAA[/math]
[math]A \rightarrow e[/math]

Упростим грамматику, заменив [math]A[/math] на [math]S[/math] (очевидно, она не поменяется), и получим в результате [math]\Gamma = \langle\{i,e\}, \{S\}, S, \{S \rightarrow iSS | e\}\rangle[/math]

Эквивалентность языков МП-автоматов и КС-языков

Теорема (об эквивалентности языков МП-автоматов и КС-языков):
Множество языков, допускаемых МП-автоматами, совпадает с множеством контекстно-свободных языков.
Доказательство:
[math]\triangleright[/math]
Первая теорема гласит, что [math] \mathrm{CFG} \subseteq \mathrm{PDA} [/math], а вторая — что [math] \mathrm{PDA} \subseteq \mathrm{CFG} [/math]. Таким образом, [math] \mathrm{PDA} = \mathrm{CFG} [/math].
[math]\triangleleft[/math]

Следствия

Утверждение:
Для любого МП-автомата с допуском по пустому стеку существует эквивалентный МП-автомат с одним состоянием.
[math]\triangleright[/math]
Построим КС-грамматику по данному автомату, затем по полученной грамматике построим МП-автомат, как указано выше. Заметим, что этот автомат будет иметь одно состояние, что и требовалось доказать.
[math]\triangleleft[/math]
Утверждение:
Для любого МП-автомата с допуском по пустому стеку существует эквивалентный МП-автомат, в любом переходе которого на стек кладётся не больше двух символов.
[math]\triangleright[/math]
Построим КС-грамматику по данному автомату и приведём её к нормальной форме Хомского. Затем по полученной грамматике построим МП-автомат, как указано выше. Заметим, что в нормальной форме Хомского правые части всех правил имеют длину не больше двух, поэтому в любом переходе в полученном автомате на стек кладётся не больше двух символов.
[math]\triangleleft[/math]
Утверждение:
Для любого МП-автомата существует эквивалентный МП-автомат с допуском по пустому стеку без [math]\varepsilon[/math]-переходов.
[math]\triangleright[/math]
Построим КС-грамматику по данному автомату, затем по полученной грамматике построим МП-автомат, как указано выше. Заметим, что этот автомат не будет иметь [math]\varepsilon[/math]-переходов, что и требовалось доказать.
[math]\triangleleft[/math]

См. также

Источники информации

  • Wikipedia — PDA and context-free languages
  • Введение в теорию автоматов, языков и вычислений / Хопкрофт Д., Мотвани Р., Ульман Д. — М.:Издательский дом «Вильямс», 2002. с. 251. — ISBN 5-8459-0261-4
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Совпадение_множества_языков_МП-автоматов_и_контекстно-свободных_языков&oldid=83024»