Материал из Викиконспекты
| НЕТ ВОЙНЕ
|
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
Антивоенный комитет России
|
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
|
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.
|
В троичной логике "лжи" и "истине" соответствует [math]-[/math] и [math]+[/math]. Третьему состоянию соответствует [math]0[/math].
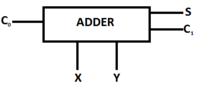
Мы будем рассматривать простую троичную функциональную схему — троичный сумматор. В нём используются такие обозначения: [math]\{0, 1, 2\}[/math] (несимметричная троичная система счисления).
Полусумматор состоит из двух частей: сложения по модулю [math]3[/math] и переноса в следующий разряд.
Логическое сложение по модулю [math]3[/math] при одном неполном слагаемом
Для сложения одного троичного разряда с разрядом переноса.
Результат не меняется при перемене мест операндов.
| [math]\bf{x_1=x}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_0=y}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{s}[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
Разряд переноса при сложении с неполным слагаемым
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
| [math]\bf{x_1=x}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_0=y}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{c}[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
Троичный полусумматор с одним неполным слагаемым
Первая ступень полного троичного сумматора.
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
| [math]\bf{x_1=x}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_0=y}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{sum}[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{transfer}[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
transfer содержит разряд переноса, sum содержит сумму по модулю [math]3[/math].
Троичный полусумматор в несимметричной троичной системе счисления
Троичное логическое сложение двух троичных разрядов с разрядом переноса в несимметричной троичной системе счисления.
Результат не изменяется при перемене мест операндов.
Троичный полусумматор можно рассматривать, как объединение двух бинарных троичных функций: «логического сложения по модулю [math]3[/math] в троичной несимметричной системе счисления» и «разряд переноса при сложении двух полных троичных разрядов в троичной несимметричной системе счисления».
| [math]\bf{x_1=x}[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_0=y}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{sum}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{c_{transfer}}[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]c_{transfer}[/math] — перенос в следующий разряд, несимметричный.
sum — сумма по модулю [math]3[/math], несимметричная.
Полное троичное логическое сложение с переносом в несимметричной троичной системе счисления
Полный троичный одноразрядный сумматор является неполной тернарной троичной логической функцией, так как в разряде переноса только два значения [math]0[/math] и [math]1[/math].
Результат не изменяется при перемене мест операндов.
| [math]\bf{x_0}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{x_1}[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_2}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{sum}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{transfer}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
См. такжеИсточники информации