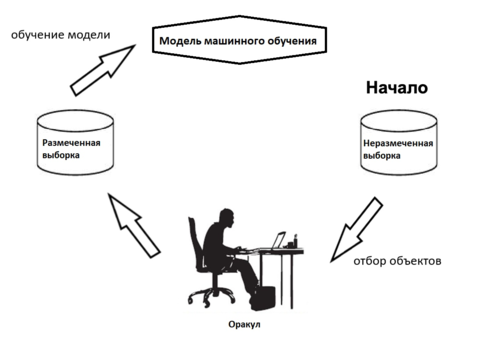
Активное обучение
Активное обучение (англ. active learning) — область машинного обучения, где алгоритм взаимодействует с некоторым источником информации, или оракулом, способным размечать запрошенные данные.
Зачастую обращение к оракулу затратно по времени или другим ресурсам, и требуется решить задачу, минимизируя количество обращений к оракулу.
Вызов оракула обычно сопровождается привлечением человека или даже группы людей. В этой роли может выступать эксперт, размечающий текстовые документы, изображения или видеозаписи. Помимо временных затрат могут возникнуть и значительные финансовые, например, исследование химического соединения или реакции.
В связи с этим одной из центральных задач активного обучения становится отбор объектов (англ. sampling) — выбор тех объектов, которые следует отправить оракулу для получения достоверной информации об их классификации. От грамотности отбора зависит время работы алгоритма, качество классификации и затраты на внешние ресурсы.
Ниже будет рассматриваться задача классификации для активного обучения, но следует отметить, что задача регрессии формализуется аналогично.
Содержание
Постановка задачи классификации для активного обучения
Дано множество неразмеченных данных:
$X = \{x_1, ..., x_n\}$,
Множество меток:
$Y = \{y_1, ..., y_m\}$,
Оракул:
$O : X \rightarrow Y$ — функция, которая по объекту возвращает его метку.
Требуется восстановить функцию $a : X \rightarrow Y$, минимизируя количество обращений к оракулу.
На каждой итерации алгоритм фиксирует три множества:
- $X_{unlabeled}$ — множество еще не размеченных объектов.
- $X_{labeled}$ — множество размеченных.
- $X_{query}$ — множество объектов, которые подаются на вход оракулу. Заметим, что не всегда $X_{query} \subset X_{unlabeled}$, поскольку алгоритм может сам синтезировать объекты.
Основные стратегии
- Отбор объектов из выборки (англ. pool-based active learning). Имеется некоторая выборка, и алгоритм использует объекты из нее в качестве запросов к оракулу. В данной стратегии каждому объекту присваивается степень информативности — сколько выгоды принесет информация об истинной метке объекта, и оракулу отправляются самые информативные объекты. Описанные ниже методы отбора объектов имеют отношение именно к этой стратегии.
- Отбор объектов из потока (англ. selective sampling). Алгоритм пользуется не статической выборкой, а потоком данных, и для каждого объекта из потока принимается решение, запрашивать оракула на этом объекте или нет. В случае, если принято решение запросить оракула, объект и его метка используются в дальнейшем обучении модели, в противном случае объект просто отбрасывается. В отличие от отбора объектов из выборки отбор из потока не строит никаких предположений насчет плотности распределения объектов, не хранит сами объекты и работает значительно быстрее.
- Синтез объектов (англ. query synthesis). Вместо использования заранее заданных объектов, алгоритм сам конструирует объекты и подает их на вход оракулу. Например, если объекты — это вектора в n-мерном пространстве, разделенные гиперплоскостью и решается задача бинарной классикации, имеет смысл давать оракулу на вход синтезированные вектора, близкие к границе.
Методы отбора объектов
Выбор по степени неуверенности
Выбор по степени неуверенности (англ. uncertainty sampling) — метод отбора объектов из выборки, где самыми информативными объектами считаются те, на которых текущий алгоритм меньше всего уверен в верности классификации. Для этого необходимо задать меру неуверенности в классификации на каждом объекте.
Зафиксируем модель на некотором этапе обучения и обозначим за $P(y | x)$ вероятность того, что объект $x$ принадлежит классу $y$. Приведем основные меры неуверенности для текущей классификации:
- Максимальная энтропия (англ. maximum entropy)
- Энтропия классификации на объекте $x$:
- $\Phi_{ENT}(x) = - \sum\limits_y{P(y | x) \log{P(y | x)}}$.
- Чем больше энтропия — тем больше неуверенность в классификации.
- Минимальный отступ (англ. smallest margin)
- Отступ (англ. margin) от $y_1$ — самого вероятного класса до $y_2$ — второго по вероятности класса:
- $\Phi_{M}(x) = P(y_1 | x) - P(y_2 | x)$.
- Очевидно, что если отступ велик, то велика и уверенность, потому что один класс заметно выигрывает у всех остальных. Поэтому имеет смысл запрашивать оракула на объектах с минимальным отступом.
- Минимальная уверенность (англ. least confidence)
- Функция неуверенности:
- $\Phi_{LC}(x) = 1 - P(y_1 | x)$,
- $y_1$ — наиболее вероятный класс. Интересующие нас объекты — объекты с минимальной уверенностью, то есть с максимальным $\Phi_{LC}$.
Заметим, что в случае бинарной классификации эти методы эквивалентны.
Взвешивание по плотности
Одной из проблем описанного выше метода может являться то, что алгоритм часто будет отдавать оракулу шумы — те объекты, которые не соответствуют основному распределению в выборке. Так как шумы являются нетипичными в контексте выборки объектами, модель может быть неуверена в их классификации, в то время как для решения основной задачи их классификация не очень полезна. Вокруг шумов плотность распределения мала, и вследствие этого применяется эвристика взвешивание по плотности где предпочтение отдается тем объектам, в которых плотность больше.
Таким образом, наиболее информативными объектами будут считаться:
$x_{informative} = arg \max\limits_x{\Phi(x) p(x)}$,
где $\Phi(x)$ — мера неуверенности, а $p(x)$ — эмпирическая плотность в точке $x$.
Отбор по несогласию в комитете
Отбор по несогласию в комитете (англ. query by comittee) — метод, в котором алгоритм оперирует не одной моделью, а сразу несколькими, которые формируют комитет. Каждая из моделей обучена на размеченном множестве и принимает участие в общем голосовании на неразмеченных объектах. Идея состоит в том, что те объекты, на которых модели более всего расходятся в своих решениях, являются самыми информативными.
Множество моделей — $A^T = \{a_1, .., a_T\}$.
Алгоритм выбирает те объекты, на которых достигается максимум энтропии:
$x_{informative} = arg \min\limits_x{P(y | x) \log{P(y | x)}}$.
Здесь $P(y | x) = \frac{1}{T} \sum\limits_{a \in A^T}{[a(x) = y]}$.
Сокращение размерности пространства решений
Сокращение размерности пространства решений (англ. version space reduction) подразумевает выбор объектов, которые максимально сокращают пространство возможных решений.
Рассмотрим простой частный случай: пусть имеется выборка точек на отрезке длины $l$, для которых требуется найти пороговый классификатор. Это означает, что заранее известна линейная разделимость выборки — то есть существует точка $t$, такая что точки $x < t$ принадлежат одному классу, а $x > t$ — другому. Наивным решением было бы разбиение отрезка на $k$ равных подотрезков, чтобы отправить оракулу по одной точке из каждого подотрезка и получить верный ответ с точностью $\dfrac{l}{k}$. Гораздо лучшим решением является бинарный поиск, который на каждой итерации сокращает пространство возможных решений вдвое, и необходимая точность $d$ достигается за $\log{\dfrac{l}{d}}$ запросов.
Максимизация ожидаемого влияния на модель
Пусть текущая модель имеет параметр $\theta$, который мы стремимся оптимизировать, чтобы уменьшить функцию потерь $L$. Тогда имеет смысл запрашивать те объекты, которые максимизируют влияние на модель (англ. expected model change). Степень влияния можно оценивать градиентом функционала потерь — $\nabla_\theta L$. Тогда мера информативности объекта:
$\Phi(x) = \sum\limits_y{P(y | x) \cdot || \nabla_\theta L_{+(x, y)} ||}$.
Здесь $L_{+(x, y)}$ обозначает функцию потерь на выборке дополненной парой $(x, y)$. При этом естественно предполагать, что на каждой итерации модель обучена, и параметр $\theta$ оптимален, что значит, что $\nabla_\theta L \simeq 0$. Заметим также, что если $L$ линейно зависит от одномерных функций потерь по каждому объекту, например $L$ — среднее квадратичное отклонение, тогда остается посчитать градиент $L$ всего в одной точке — $x$, поскольку $L_{+(x, y)} = L_T + L_{(x, y)} \simeq L_{(x, y)}$ вместо подсчета $L$ на всем тренировочном множестве $T$.
Ожидаемое сокращение ошибки
Идея данного метода (англ. expected error reduction) состоит в том, чтобы выбрать такой объект, после добавления которого в обучающее множество, максимизируется уверенность в классификации неразмеченной выборки. Уверенность в классификации выражается следующей функцией:
$\Phi(x) = \sum\limits_{y \in Y}{(P(y | x) \sum\limits_{u \in X}{P(a_{xy}(u) | u)})}$.
Формула выше может быть интерпретирована как матожидание уверенности нового классификатора (учитывающего метку объекта $x$) на оставшемся неразмеченном множестве. Существует мнение, что этот метод более устойчив, чем предыдущие, поскольку он не склонен подавать на вход оракулу шумы, и явно увеличивает уверенность классификатора.
Активное обучение с исследовательскими действиями
У рассмотренных выше стратегий отбора есть недостатки: в пространстве $X$ могут оставаться неисследованные области, вследствие чего снижается качество и увеличивается время обучения. Эвристикой, позволяющей решить эту проблему, является выбор случайных объектов, комбинированный с детерминированным выбором по степени информативности.
Есть два алгоритма обертки над любой стратегией отбора — алгоритм $\varepsilon$-active и алгоритм экспоненциального градиента (англ. exponential gradient). Алгоритм $\varepsilon$-active — это базовый вариант, в котором предлагается на каждой итерации производить следующие шаги:
- Выбрать неразмеченный объект $x$ случайно с вероятностью $\varepsilon$ или $x = arg \max\limits_{u \in X}{\Phi(u)}$ с вероятностью $1 - \varepsilon$.
Здесь $\Phi(u)$ обозначает степень неуверенности на объекте $u$. - Запросить оракула на объекте $x$ и получить его метку $y$.
- Дообучить текущую модель на еще одном примере $\langle x, y \rangle$.
Алгоритм экспоненциального градиента является улучшением $\varepsilon$-active. Идея состоит в том, что параметр $\varepsilon$ выбирается случайно из конечного множества, где каждому элементу присвоены вероятности. По ходу алгоритма экспоненциально увеличиваются вероятности наиболее успешных $\varepsilon$, что несколько напоминает алгоритм Adaboost по принципу работы.