Полином Жегалкина — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 58 промежуточных версий 15 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Полином Жегалкина''' — полином с коэффициентами вида 0 и 1, где в качестве произведения | + | '''Полином Жегалкина''' (англ. ''Zhegalkin polynomial'') — полином с коэффициентами вида <tex>0</tex> и <tex>1</tex>, где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве средства для представления [[Определение булевой функции|функций булевой логики]]. Полином Жегалкина имеет следующий вид: |
| + | <tex>P = a_{000\ldots000} \oplus a_{100\ldots0} x_1 \oplus a_{010\ldots0} x_2 \oplus \ldots \oplus a_{00\ldots01} x_n \oplus a_{110\ldots0} x_1 x_2 \oplus \ldots \oplus a_{00\ldots011} x_{n-1} x_n \oplus \ldots \oplus a_{11\ldots1} x_1 x_2 \ldots x_n </tex> | ||
| − | + | == Полнота == | |
| − | = | ||
| − | По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали | + | По [[Теорема Поста о полной системе функций|теореме Поста]], чтобы система булевых функций была полной, надо, чтобы в ней существовали |
| − | + | #Хотя бы одна функция, не сохраняющая <tex>0</tex>; | |
| − | + | #Хотя бы одна функция, не сохраняющая <tex>1</tex>; | |
| − | + | #Хотя бы одна нелинейная функция; | |
| − | + | #Хотя бы одна немонотонная функция; | |
| − | + | #Хотя бы одна несамодвойственная функция. | |
| − | + | Исходя из этого, система функций <tex>\bigl\langle \wedge, \oplus, 1 \bigr\rangle</tex> является полной: | |
| + | |||
| + | {| class="wikitable" style="width:8cm" border="1" | ||
| + | |-align="center" bgcolor=#EEEEFF | ||
| + | !<tex>x_0</tex>||<tex>x_1</tex>||<tex>\ldots</tex>||<tex>x_n</tex> | ||
| + | |<tex>1</tex>||<tex>\land</tex>||<tex>\oplus</tex> | ||
| + | |-align="center" | ||
| + | !<tex>0</tex>||<tex>0</tex>||<tex>\ldots</tex>||<tex>0</tex> | ||
| + | |<tex>1</tex>||<tex>0</tex>||<tex>0</tex> | ||
| + | |-align="center" | ||
| + | !<tex>1</tex>||<tex>0</tex>||<tex>\ldots</tex>||<tex>0</tex> | ||
| + | |<tex>1</tex>||<tex>0</tex>||<tex>1</tex> | ||
| + | |-align="center" | ||
| + | !<tex>\vdots</tex>||<tex>\vdots</tex>||<tex>\vdots</tex>||<tex>\vdots</tex> | ||
| + | |<tex>\vdots</tex>||<tex>\vdots</tex>||<tex>\vdots</tex> | ||
| + | |-align="center" | ||
| + | !<tex>1</tex>||<tex>1</tex>||<tex>\ldots</tex>||<tex>1</tex> | ||
| + | |<tex>1</tex>||<tex>1</tex>||<tex>0</tex> | ||
| + | |-align="center" | ||
| + | !colspan="4"|[[Полные_системы_функций._Теорема_Поста_о_полной_системе_функций#.D0.97.D0.B0.D0.BC.D0.BA.D0.BD.D1.83.D1.82.D1.8B.D0.B5_.D0.BA.D0.BB.D0.B0.D1.81.D1.81.D1.8B_.D0.B1.D1.83.D0.BB.D0.B5.D0.B2.D1.8B.D1.85_.D1.84.D1.83.D0.BD.D0.BA.D1.86.D0.B8.D0.B9|Сохраняет 0]] | ||
| + | |<tex>0</tex>||<tex>1</tex>||<tex>1</tex> | ||
| + | |-align="center" | ||
| + | !colspan="4"|[[Полные_системы_функций._Теорема_Поста_о_полной_системе_функций#.D0.97.D0.B0.D0.BC.D0.BA.D0.BD.D1.83.D1.82.D1.8B.D0.B5_.D0.BA.D0.BB.D0.B0.D1.81.D1.81.D1.8B_.D0.B1.D1.83.D0.BB.D0.B5.D0.B2.D1.8B.D1.85_.D1.84.D1.83.D0.BD.D0.BA.D1.86.D0.B8.D0.B9|Сохраняет 1]] | ||
| + | |<tex>1</tex>||<tex>1</tex>||<tex>0</tex> | ||
| + | |-align="center" | ||
| + | !colspan="4"|[[Полные_системы_функций._Теорема_Поста_о_полной_системе_функций#.D0.97.D0.B0.D0.BC.D0.BA.D0.BD.D1.83.D1.82.D1.8B.D0.B5_.D0.BA.D0.BB.D0.B0.D1.81.D1.81.D1.8B_.D0.B1.D1.83.D0.BB.D0.B5.D0.B2.D1.8B.D1.85_.D1.84.D1.83.D0.BD.D0.BA.D1.86.D0.B8.D0.B9|Самодвойственная]] | ||
| + | |<tex>0</tex>||<tex>0</tex>||<tex>0</tex> | ||
| + | |-align="center" | ||
| + | !colspan="4"|[[Полные_системы_функций._Теорема_Поста_о_полной_системе_функций#.D0.97.D0.B0.D0.BC.D0.BA.D0.BD.D1.83.D1.82.D1.8B.D0.B5_.D0.BA.D0.BB.D0.B0.D1.81.D1.81.D1.8B_.D0.B1.D1.83.D0.BB.D0.B5.D0.B2.D1.8B.D1.85_.D1.84.D1.83.D0.BD.D0.BA.D1.86.D0.B8.D0.B9|Монотонная]] | ||
| + | |<tex>1</tex>||<tex>1</tex>||<tex>0</tex> | ||
| + | |-align="center" | ||
| + | !colspan="4"|[[Полные_системы_функций._Теорема_Поста_о_полной_системе_функций#.D0.97.D0.B0.D0.BC.D0.BA.D0.BD.D1.83.D1.82.D1.8B.D0.B5_.D0.BA.D0.BB.D0.B0.D1.81.D1.81.D1.8B_.D0.B1.D1.83.D0.BB.D0.B5.D0.B2.D1.8B.D1.85_.D1.84.D1.83.D0.BD.D0.BA.D1.86.D0.B8.D0.B9|Линейная]] | ||
| + | |<tex>1</tex>||<tex>0</tex>||<tex>1</tex> | ||
| + | |} | ||
| − | + | На основе этой системы и строятся полиномы Жегалкина. | |
| − | |||
| + | == Существование и единственность представления (теорема Жегалкина) == | ||
| + | {{Теорема | ||
| + | |author=Жегалкина | ||
| + | |statement= | ||
| + | Каждая булева функция единственным образом представляется в виде полинома Жегалкина. | ||
| + | |proof= | ||
| + | Заметим, что различных булевых функций от <tex>n</tex> переменных <tex>2^{2^n}</tex> штук. При этом конъюнкций вида <tex>x_{i_1} \ldots x_{i_k}</tex> существует ровно <tex>2^n</tex>, так как из <tex>n</tex> возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит <tex>0</tex> или <tex>1</tex>, то есть существует <tex>2^{2^n}</tex> различных полиномов Жегалкина от <tex>n</tex> переменных. | ||
| + | |||
| + | Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом. | ||
| + | }} | ||
== Построение полинома Жегалкина == | == Построение полинома Жегалкина == | ||
| Строка 23: | Строка 65: | ||
Существует несколько способов построения полинома Жегалкина. | Существует несколько способов построения полинома Жегалкина. | ||
| − | + | === По таблице истинности === | |
| + | Пусть для функции <tex>f(x_1,x_2,\ldots,x_n)</tex> задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что <tex> a \oplus 1 = \bar{a}</tex>, а <tex> a \oplus 0 = a</tex>. За каждую подстановку находим только один коэффициент. | ||
| + | |||
| + | '''Пример:''' | ||
| + | Дана функция <tex>f(x_1,x_2,x_3,x_4)</tex> и её таблица истинности: | ||
| + | |||
| + | {| class="wikitable" style="width:8cm" border="1" | ||
| + | |- | ||
| + | !class="dark" style="font-weight:normal"| <tex>x_1</tex> | ||
| + | !class="dark" style="font-weight:normal"| <tex>x_2</tex> | ||
| + | !class="dark" style="font-weight:normal"| <tex>x_3</tex> | ||
| + | !class="dark" style="font-weight:normal"| <tex>x_4</tex> | ||
| + | !class="dark" style="font-weight:normal"| <tex>f(x_1,x_2,x_3,x_4)</tex> | ||
| + | |- align="center" | ||
| + | ||0||0||0||0||0 | ||
| + | |- align="center" | ||
| + | ||0||0||0||1||0 | ||
| + | |- align="center" | ||
| + | ||0||0||1||0||0 | ||
| + | |- align="center" | ||
| + | ||0||0||1||1||0 | ||
| + | |- align="center" | ||
| + | ||0||1||0||0||0 | ||
| + | |- align="center" | ||
| + | ||0||1||0||1||0 | ||
| + | |- align="center" | ||
| + | ||0||1||1||0||1 | ||
| + | |- align="center" | ||
| + | ||0||1||1||1||0 | ||
| + | |- align="center" | ||
| + | ||1||0||0||0||1 | ||
| + | |- align="center" | ||
| + | ||1||0||0||1||0 | ||
| + | |- align="center" | ||
| + | ||1||0||1||0||0 | ||
| + | |- align="center" | ||
| + | ||1||0||1||1||1 | ||
| + | |- align="center" | ||
| + | ||1||1||0||0||1 | ||
| + | |- align="center" | ||
| + | ||1||1||0||1||0 | ||
| + | |- align="center" | ||
| + | ||1||1||1||0||1 | ||
| + | |- align="center" | ||
| + | ||1||1||1||1||0 | ||
| + | |} | ||
| + | Построим для неё полином Жегалкина: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = a_{0000} \oplus a_{1000} x_1 \oplus a_{0100} x_2 \oplus a_{0010} x_3 \oplus a_{0001} x_4 \oplus a_{1100} x_1 x_2 \oplus a_{1010} x_1 x_3 \oplus a_{1001} x_1 x_4 \oplus a_{0110} x_2 x_3 \oplus a_{0101} x_2 x_4 \oplus a_{0011} x_3 x_4 \oplus a_{1110} x_1 x_2 x_3 \oplus a_{1101} x_1 x_2 x_4 \oplus a_{1011} x_1 x_3 x_4 \oplus a_{0111} x_2 x_3 x_4 \oplus a_{1111} x_1 x_2 x_3 x_4</tex> | ||
| + | |||
| + | Так как <tex>f(0,0,0,0) = 0</tex>, то <tex>a_{0000} = 0</tex>. | ||
| + | Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы: | ||
| + | |||
| + | <tex>f(1,0,0,0) = a_{0000} \oplus a_{1000} = 1,</tex> следовательно <tex>a_{1000} = 1</tex> | ||
| + | |||
| + | <tex>f(0,1,0,0) = a_{0000} \oplus a_{0100} = 0,</tex> следовательно <tex>a_{0100} = 0</tex> | ||
| + | |||
| + | <tex>f(0,0,1,0) = a_{0000} \oplus a_{0010} = 0,</tex> следовательно <tex> a_{0010} = 0</tex> | ||
| + | |||
| + | <tex>f(0,0,0,1) = a_{0000} \oplus a_{0001} = 0,</tex> следовательно <tex> a_{0001} = 0</tex> | ||
| + | |||
| + | <tex>f(1,1,0,0) = a_{0000} \oplus a_{1000} \oplus a_{0100} \oplus a_{1100} = 1,</tex> следовательно <tex> a_{1100} = 0</tex> | ||
| + | |||
| + | <tex>f(1,0,1,0) = a_{0000} \oplus a_{1000} \oplus a_{0010} \oplus a_{1010} = 0, </tex> следовательно <tex> a_{1010} = 1</tex> | ||
| + | |||
| + | <tex>f(1,0,0,1) = a_{0000} \oplus a_{1000} \oplus a_{0001} \oplus a_{1001} = 0, </tex> следовательно <tex> a_{1001} = 1</tex> | ||
| + | |||
| + | <tex>f(0,1,1,0) = a_{0000} \oplus a_{0100} \oplus a_{0010} \oplus a_{0110} = 1, </tex> следовательно <tex> a_{0110} = 1</tex> | ||
| + | |||
| + | <tex>f(0,1,0,1) = a_{0000} \oplus a_{0100} \oplus a_{0001} \oplus a_{0101} = 0, </tex> следовательно <tex> a_{0101} = 0</tex> | ||
| + | |||
| + | <tex>f(0,0,1,1) = a_{0000} \oplus a_{0010} \oplus a_{0001} \oplus a_{0011} = 0, </tex> следовательно <tex> a_{0011} = 0</tex> | ||
| + | |||
| + | <tex>f(1,1,1,0) = a_{0000} \oplus a_{1000} \oplus a_{0100} \oplus a_{0010} \oplus a_{1100} \oplus a_{1010} \oplus a_{0110} \oplus a_{1110} = 1, </tex> следовательно <tex> a_{1110} = 0</tex> | ||
| + | |||
| + | <tex>f(1,1,0,1) = a_{0000} \oplus a_{1000} \oplus a_{0100} \oplus a_{0001} \oplus a_{1100} \oplus a_{1001} \oplus a_{0101} \oplus a_{1101} = 0, </tex> следовательно <tex> a_{1101} = 0</tex> | ||
| + | |||
| + | <tex>f(1,0,1,1) = a_{0000} \oplus a_{1000} \oplus a_{0010} \oplus a_{0001} \oplus a_{1010} \oplus a_{1001} \oplus a_{0011} \oplus a_{1011} = 1, </tex> следовательно <tex> a_{1011} = 0</tex> | ||
| + | |||
| + | <tex>f(0,1,1,1) = a_{0000} \oplus a_{0100} \oplus a_{0010} \oplus a_{0001} \oplus a_{0110} \oplus a_{0101} \oplus a_{0011} \oplus a_{0111} = 0, </tex> следовательно <tex> a_{0111} = 1</tex> | ||
| + | |||
| + | <tex>f(1,1,1,1) = a_{0000} \oplus a_{1000} \oplus a_{0100} \oplus a_{0010} \oplus a_{0001} \oplus a_{1100} \oplus a_{1010} \oplus a_{1001} \oplus a_{0110} \oplus a_{0101} \oplus a_{0011} \oplus a_{1110} \oplus a_{1101} \oplus a_{1011} \oplus a_{0111} \oplus a_{1111} = 0, </tex> следовательно <tex> a_{1111} = 1</tex> | ||
| + | |||
| + | Таким образом, полином Жегалкина выглядит так: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = x_1 \oplus x_1 x_3 \oplus x_1 x_4 \oplus x_2 x_3 \oplus x_2 x_3 x_4 \oplus x_1 x_2 x_3 x_4</tex> | ||
| + | |||
| + | === Преобразование [[Определение_булевой_функции#Дизъюнктивная нормальная форма (ДНФ)|дизъюнктивной нормальной формы]] === | ||
| + | Этот способ основан на том, что <tex> X \oplus 1 = \bar{X} </tex>. Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило де Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю (так как <tex> X \oplus X = 0 </tex>), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу: | ||
| + | <tex> A \lor B = AB \oplus A \oplus B </tex> <tex> (1) </tex>. | ||
| + | |||
| + | Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ. | ||
| + | |||
| + | '''Пример:''' | ||
| + | Дана функция в ДНФ <tex> f(x_1,x_2,x_3,x_4) = (x_1 \land x_2 \land \neg x_3 \land x_4) \lor (\neg x_1 \land \neg x_4) \lor (x_1 \land x_2) \lor x_2 </tex>, построим полином Жегалкина. | ||
| + | |||
| + | Запишем функцию так: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = x_1 x_2 \neg x_3 x_4 + \neg x_1 \neg x_4 + x_1 x_2 + x_2</tex>; | ||
| + | |||
| + | Сгруппируем слагаемые и воспользуемся преобразованием (1): | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = (x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4 \oplus x_1 x_2 \neg x_3 x_4 \neg x_1 \neg x_4) + (x_1 x_2 \oplus x_2 \oplus \oplus x_1 x_2 x_2)</tex> | ||
| + | |||
| + | Воспользуемся свойствами конъюнкции <tex>A \land A = A</tex> и <tex>\neg A \land A = 0</tex>, а также тем, что <tex>A \oplus A = 0</tex>, и упростим выражение: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = (x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4) + x_2</tex> | ||
| + | |||
| + | Ещё раз воспользуемся преобразованием (1): | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4 \oplus x_2 \oplus (x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4) x_2</tex> | ||
| + | |||
| + | Раскроем скобку по алгебраическим правилам: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = x_1 x_2 \neg x_3 x_4 \oplus \neg x_1 \neg x_4 \oplus x_2 \oplus x_1 x_2 x_2 \neg x_3 x_4 \oplus \neg x_1 x_2 \neg x_4</tex> | ||
| + | |||
| + | Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = \neg x_1 \neg x_4 \oplus x_2 \oplus \neg x_1 x_2 \neg x_4</tex> | ||
| + | |||
| + | Заменим отрицание на прибавление <tex>1</tex>: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = (x_1 \oplus 1) (x_4 \oplus 1) \oplus x_2 \oplus (x_1 \oplus 1) x_2 (x_4 \oplus 1)</tex> | ||
| + | |||
| + | Раскроем скобки: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = x_1 x_4 \oplus x_1 \oplus x_4 \oplus 1 \oplus x_2 \oplus x_1 x_2 x_4 \oplus x_1 x_2 \oplus x_2 x_4 \oplus x_2</tex> | ||
| + | |||
| + | Выкинем парные слагаемые и получим окончательную формулу: | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = x_1 x_2 x_4 \oplus x_1 x_2 \oplus x_1 x_4 \oplus x_2 x_4 \oplus x_1 \oplus x_4 \oplus 1</tex> | ||
| + | |||
| + | === Метод треугольника === <!-- Да, копипаста с википедии, и что? Метод же прост и удобен --> | ||
| + | Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами: | ||
| + | # Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от <tex>000\ldots00</tex> до <tex>111\ldots11</tex>. | ||
| + | # Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности. | ||
| + | # Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже. | ||
| + | # Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности. | ||
| + | # Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке <tex>111</tex> соответствует член <tex>ABC</tex>, ячейке <tex>101</tex> — член <tex>AC</tex>, ячейке <tex>010</tex> — член <tex>B</tex>, ячейке <tex>000</tex> — член <tex>1</tex> и т.д. | ||
| + | # Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина. | ||
| + | |||
| + | Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций. | ||
| + | |||
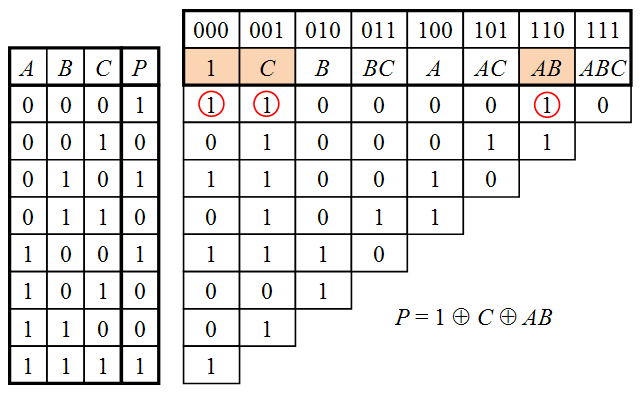
| + | Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных <tex>P(A,B,C)</tex> показан на рисунке. | ||
| + | |||
| + | [[Файл:Преобразование таблицы истинности в полином Жегалкина методом треугольника.gif]] | ||
| + | |||
| + | Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца <tex>''P''</tex> таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2. | ||
| + | |||
| + | Таким образом, в первом столбце сверху записан коэффициент <tex> a_0 = P(0,0,0) </tex>, | ||
| + | |||
| + | во втором — <tex> a_1 = P(0,0,0) \oplus P(0,0,1) </tex>, | ||
| + | |||
| + | в третьем — <tex> a_2 = P(0,0,0) \oplus P(0,0,1) \oplus P(0,0,1) \oplus P(0,1,0) = P(0,0,0) \oplus P(0,1,0) </tex>, | ||
| + | |||
| + | в четвёртом — | ||
| + | |||
| + | <tex> a_3 = P(0,0,0) \oplus P(0,0,1) \oplus P(0,0,1) \oplus P(0,0,1) \oplus P(0,1,0) \oplus P(0,1,0) \oplus P(0,1,0) \oplus P(0,1,1) = P(0,0,0) \oplus P(0,1,0) \oplus P(0,0,1) \oplus P(0,1,1), </tex> | ||
| + | |||
| + | и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически. | ||
| + | |||
| + | === Преобразование Мёбиуса === | ||
| + | Пусть задана [[Определение булевой функции|булева функция]] <tex>f: B^n \rightarrow B, \;\; B=\{ 0; 1 \}</tex>. | ||
| + | Любая булева функция представима в виде полинома Жегалкина, притом единственным образом. | ||
| + | |||
| + | Пусть <tex> i = (i_1, i_2, \ldots i_n), \;\; i_k \in \{0 ; 1\}</tex>, и введем обозначение <tex> x ^{i_k} \sim \left\{\begin{matrix} x, \;\; i_k=1 | ||
| + | \\ 1, \;\; i_k=0 | ||
| + | \end{matrix}\right. </tex> | ||
| + | |||
| + | Тогда полином Жегалкина можно записать как: | ||
| + | <tex> f(x) = \bigoplus\limits_i \alpha_i \cdot x_1^{i_1} \cdot x_2^{i_2} \cdot</tex> <tex>\ldots</tex> <tex>\cdot x_n^{i_n}</tex>, где <tex>\alpha_i \in \{ 0; 1 \}</tex>. | ||
| + | |||
| + | Множество коэффициентов <tex>\{\alpha _i\}</tex> можно рассматривать как функцию <tex>\alpha</tex>, заданной на множестве индексов <tex> i = (i_1, i_2, \ldots i_n)</tex>, то есть <tex>\alpha: i \mapsto \alpha_i</tex>. | ||
| + | |||
| + | Очевидно, функцию <tex> f </tex> можно записать и следующим образом: <tex> f(x) = \bigoplus \limits_i \alpha_i \cdot [x_1 , \; </tex> если <tex> \;\; i_1] \cdot [x_2 , \; </tex> если <tex> \;\; i_2] \cdot</tex> <tex>\ldots</tex> <tex>\cdot [x_n , \; </tex> если <tex> \;\; i_n]</tex>. | ||
| + | |||
| + | Тут запись <tex>[x_k , \; </tex> если <tex> \; i_k]</tex> означает, что элелемент <tex> x_k </tex> присутствует в соответствующем члене полинома только если <tex> i_k = 1 </tex>. | ||
| + | Тогда если для какого-то <tex>x</tex>, <tex>i \succ x*</tex> ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. | ||
| + | Отсюда ясно, что <tex> f(x) = \bigoplus \limits_{i \preceq x} \alpha_i </tex> <tex> (2) </tex> | ||
| + | Найдем отображение <tex> f \mapsto \alpha</tex> (То есть такое, которое по заданной функции вычисляет значения всех коэффициентов). | ||
| + | |||
| + | <tex>*</tex> <tex>i \succ x</tex> обозначает, что <tex>x</tex> "меньше" <tex>i</tex> как последовательность бит | ||
| + | |||
| + | {{Теорема | ||
| + | |statement=Пусть задана функция <tex> f </tex>. Тогда функцию <tex> \alpha_x </tex> можно найти по формуле: <tex>\alpha_x = \bigoplus \limits_{j\preceq x} f(j)</tex> <tex> (3) </tex>. | ||
| + | ||proof=Докажем при помощи индукции по количеству единиц в векторе <tex> x </tex> ( иначе говоря, по сумме <tex>x_1+x_2+</tex><tex>\ldots</tex><tex>+x_n</tex> ) и для удобства обозначим это количество единиц(сумму) <tex> wt(x) </tex>. | ||
| + | |||
| + | '''1)''' База: если <tex> x = 0 </tex>, то, очевидно <tex> f(0) = \alpha_0 </tex> | ||
| + | |||
| + | '''2)''' Пускай теорема справедлива для всех сумм <tex>wt(x) < k</tex>. Покажем, что в таком случае она верна и для <tex>wt(x) = k</tex>. По <tex> (2) </tex>, а далее по предположению индукции видим: <tex> f(x) = \bigoplus \limits_{i \preceq x} \alpha_i = \left [ \bigoplus \limits_{i \prec x} \bigoplus \limits_{j\preceq i} f(j) \right ] \oplus \alpha_x</tex> . | ||
| + | |||
| + | Рассмотрим сумму <tex> \left [ \bigoplus \limits_{i \prec x} \bigoplus \limits_{j\preceq i} f(j) \right ] </tex>. Каждый элемент <tex> f(j) </tex> содержится в ней, только если <tex> j \prec x </tex>, и для фиксированных <tex> j</tex> и <tex> x </tex> элемент <tex> f(j)</tex> встречается ровно столько раз, сколько существует <tex> i </tex> , таких, что <tex> j \preceq i \prec x</tex>. Несложно увидеть, что таких <tex> i </tex> существует ровно <tex> 2^{wt(x)-wt(j)}-1 </tex>, то есть нечетное количество раз. Тогда <tex> \left [ \bigoplus \limits_{i \prec x} \bigoplus \limits_{j\preceq i} f(j) \right ] = \bigoplus \limits_{j\prec x} f(j) </tex>. | ||
| + | Но тогда <tex> f(x) = \left [ \bigoplus \limits_{j\prec x} f(j) \right ] \oplus \alpha_x \Leftrightarrow f(x) \oplus \bigoplus \limits_{j\prec x} f(j) = \alpha_x \Leftrightarrow \alpha_x = \bigoplus \limits_{j\preceq x} f(j)</tex>. | ||
| + | То есть при <tex>wt(x) = k</tex> формула также выполняется, значит при любых <tex> x </tex> выполняется <tex>\alpha_x = \bigoplus \limits_{j\preceq x} f(j)</tex>. | ||
| + | |||
| + | }} | ||
| + | Отображение <tex> f \rightarrow \alpha</tex> также называется преобразованием Мёбиуса. | ||
| + | |||
| + | Видно, что <tex> (2) </tex> и <tex> (3) </tex> — это одно и тоже преобразование. Значит, если применить преобразование Мёбиуса к функции, а затем вновь применить то же преобразование к получившейся функции, тогда вновь получим исходную функцию <tex>f</tex>. То есть преобразование Мёбиуса обратно самому себе, иными словами, является инволюцией. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Определение_булевой_функции|Булевы функции]] | ||
| + | * [[Полные_системы_функций._Теорема_Поста_о_полной_системе_функций|Полные системы функций, теорема Поста]] | ||
| + | * [[СДНФ|ДНФ]] | ||
| + | * [[СКНФ|КНФ]] | ||
| + | == Источники информации == | ||
| − | + | * [http://www.stat-mat.com/?p=330 Cтатистика | Математика НГУ] | |
| + | * [http://ru.wikipedia.org/wiki/Полином_Жегалкина Википедия {{---}} Полином Жегалкина] | ||
| + | * [http://dvo.sut.ru/libr/himath/w163rabk/index.htm Е.Л Рабкин, Ю.Б. Фарфоровская, дискретная математика] | ||
| + | * Логачёв О.А, Сальников А.А., Ященко В.В. Булевы фунции в теории кодирования и криптологии — МЦНМО, 2004. - 470с. — ISBN 5-94057-117-4. | ||
| − | + | [[Категория: Дискретная математика и алгоритмы]] | |
| + | [[Категория: Булевы функции]] | ||
Текущая версия на 19:36, 4 сентября 2022
Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида и , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве средства для представления функций булевой логики. Полином Жегалкина имеет следующий вид:
Содержание
Полнота
По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали
- Хотя бы одна функция, не сохраняющая ;
- Хотя бы одна функция, не сохраняющая ;
- Хотя бы одна нелинейная функция;
- Хотя бы одна немонотонная функция;
- Хотя бы одна несамодвойственная функция.
Исходя из этого, система функций является полной:
| Сохраняет 0 | ||||||
|---|---|---|---|---|---|---|
| Сохраняет 1 | ||||||
| Самодвойственная | ||||||
| Монотонная | ||||||
| Линейная | ||||||
На основе этой системы и строятся полиномы Жегалкина.
Существование и единственность представления (теорема Жегалкина)
| Теорема (Жегалкина): |
Каждая булева функция единственным образом представляется в виде полинома Жегалкина. |
| Доказательство: |
|
Заметим, что различных булевых функций от переменных штук. При этом конъюнкций вида существует ровно , так как из возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит или , то есть существует различных полиномов Жегалкина от переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом. |
Построение полинома Жегалкина
Существует несколько способов построения полинома Жегалкина.
По таблице истинности
Пусть для функции задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что , а . За каждую подстановку находим только один коэффициент.
Пример: Дана функция и её таблица истинности:
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Построим для неё полином Жегалкина:
Так как , то . Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
следовательно
Таким образом, полином Жегалкина выглядит так:
Преобразование дизъюнктивной нормальной формы
Этот способ основан на том, что . Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило де Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю (так как ), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу: .
Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.
Пример: Дана функция в ДНФ , построим полином Жегалкина.
Запишем функцию так:
;
Сгруппируем слагаемые и воспользуемся преобразованием (1):
Воспользуемся свойствами конъюнкции и , а также тем, что , и упростим выражение:
Ещё раз воспользуемся преобразованием (1):
Раскроем скобку по алгебраическим правилам:
Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:
Заменим отрицание на прибавление :
Раскроем скобки:
Выкинем парные слагаемые и получим окончательную формулу:
Метод треугольника
Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:
- Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от до .
- Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
- Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
- Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
- Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке соответствует член , ячейке — член , ячейке — член , ячейке — член и т.д.
- Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.
Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций.
Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных показан на рисунке.
Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2.
Таким образом, в первом столбце сверху записан коэффициент ,
во втором — ,
в третьем — ,
в четвёртом —
и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически.
Преобразование Мёбиуса
Пусть задана булева функция . Любая булева функция представима в виде полинома Жегалкина, притом единственным образом.
Пусть , и введем обозначение
Тогда полином Жегалкина можно записать как: , где .
Множество коэффициентов можно рассматривать как функцию , заданной на множестве индексов , то есть .
Очевидно, функцию можно записать и следующим образом: если если если .
Тут запись если означает, что элелемент присутствует в соответствующем члене полинома только если . Тогда если для какого-то , ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. Отсюда ясно, что Найдем отображение (То есть такое, которое по заданной функции вычисляет значения всех коэффициентов).
обозначает, что "меньше" как последовательность бит
| Теорема: |
Пусть задана функция . Тогда функцию можно найти по формуле: . |
| Доказательство: |
|
Докажем при помощи индукции по количеству единиц в векторе ( иначе говоря, по сумме ) и для удобства обозначим это количество единиц(сумму) . 1) База: если , то, очевидно 2) Пускай теорема справедлива для всех сумм . Покажем, что в таком случае она верна и для . По , а далее по предположению индукции видим: . Рассмотрим сумму . Каждый элемент содержится в ней, только если , и для фиксированных и элемент встречается ровно столько раз, сколько существует , таких, что . Несложно увидеть, что таких существует ровно , то есть нечетное количество раз. Тогда . Но тогда . То есть при формула также выполняется, значит при любых выполняется . |
Отображение также называется преобразованием Мёбиуса.
Видно, что и — это одно и тоже преобразование. Значит, если применить преобразование Мёбиуса к функции, а затем вновь применить то же преобразование к получившейся функции, тогда вновь получим исходную функцию . То есть преобразование Мёбиуса обратно самому себе, иными словами, является инволюцией.
См. также
Источники информации
- Cтатистика | Математика НГУ
- Википедия — Полином Жегалкина
- Е.Л Рабкин, Ю.Б. Фарфоровская, дискретная математика
- Логачёв О.А, Сальников А.А., Ященко В.В. Булевы фунции в теории кодирования и криптологии — МЦНМО, 2004. - 470с. — ISBN 5-94057-117-4.