Простейшие методы синтеза схем из функциональных элементов — различия между версиями
м |
(Исправил ошибки) |
||
| Строка 16: | Строка 16: | ||
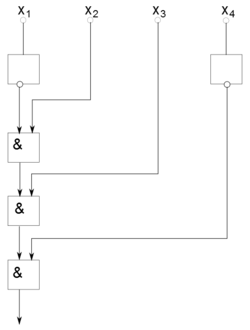
Построим данную схему следующим образом: возьмем <tex> n </tex> элементов отрицания, присоединенных к выходам, и цепочки из элементов конъюнкции, имеющих <tex> n </tex> "свободных" входов. | Построим данную схему следующим образом: возьмем <tex> n </tex> элементов отрицания, присоединенных к выходам, и цепочки из элементов конъюнкции, имеющих <tex> n </tex> "свободных" входов. | ||
| − | + | Если <tex> i </tex>-й множитель равен <tex> x_{i} </tex>, то <tex> i </tex>-й вход этой цепочки присоединяется к входу схемы. А если <tex> i </tex>-й множитель равен <tex> \bar{x}_{i} </tex>,то присоединяется к выходу <tex> i </tex>-го элемента отрицания.(рис. 1) | |
| − | Очевидно, что сложность построенной схемы | + | Очевидно, что сложность построенной схемы <tex> size_{B}(f)= n+n-1 = 2n-1 </tex>. |
Поэтому <tex> size_{B}(f)\le 2n-1 </tex>. | Поэтому <tex> size_{B}(f)\le 2n-1 </tex>. | ||
| Строка 30: | Строка 30: | ||
|statement = Для любой функции <tex> f(x_{1}, ..., x_{n}) </tex> имеет место неравенство <tex> size_{B}(f)\le n2^{n+1} </tex> | |statement = Для любой функции <tex> f(x_{1}, ..., x_{n}) </tex> имеет место неравенство <tex> size_{B}(f)\le n2^{n+1} </tex> | ||
|proof = [[Файл:Synschemes Theorem1.png|250px|thumb|right|Рис. 2]] | |proof = [[Файл:Synschemes Theorem1.png|250px|thumb|right|Рис. 2]] | ||
| − | Пусть <tex> f(x_{1},...,x_{n}) </tex> {{---}} произвольная [[Определение булевой функции|булева функция]]. Если <tex> f \ne 0 </tex>, то <tex> f </tex> может быть задана [[ДНФ|дизъюнктивной нормальной формой]] | + | Пусть <tex> f(x_{1},...,x_{n}) </tex> {{---}} произвольная [[Определение булевой функции|булева функция]]. |
| + | |||
| + | Если <tex> f = 0 </tex>, то схема строится в соответствии с представлением <tex> 0=x_{1}\wedge\overline{x}_{1} </tex>, то есть <tex> size_{B}(0) \le 2</tex>. | ||
| + | |||
| + | Если <tex> f \ne 0 </tex>, то <tex> f </tex> может быть задана [[ДНФ|дизъюнктивной нормальной формой]] | ||
::<tex> f(x_{1},...,x_{n}) = K_{1} \vee K_{2} \vee ... \vee K_{s} </tex>, | ::<tex> f(x_{1},...,x_{n}) = K_{1} \vee K_{2} \vee ... \vee K_{s} </tex>, | ||
| Строка 38: | Строка 42: | ||
::<tex> K_{j}=x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{i} </tex> | ::<tex> K_{j}=x_{1}\wedge\overline{x}_{2}\wedge{x}_{3}\wedge ... \wedge{x}_{i} </tex> | ||
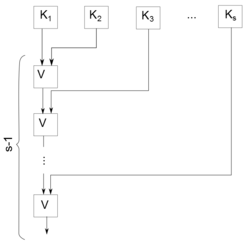
| − | Схема <tex> S </tex> для <tex> f </tex> состоит из конъюнкций <tex> K_{j} </tex> (каждая из них в соответствии с [[#Lemma1| | + | Схема <tex> S </tex> для <tex> f </tex> состоит из конъюнкций <tex> K_{j} </tex> (каждая из них в соответствии с [[#Lemma1|леммой 1]] имеет сложность не более <tex> 2n-1 </tex>) и цепочки из <tex> s-1 </tex> элемента дизъюнкции с <tex> s </tex> свободными входами. Свободные входы этой цепочки присоединяются к выходам схем для конъюнкций <tex> K_{j} </tex>.(рис. 2) Имеем |
::<tex> size_{B}(f)\le s\cdot(2n-1)+s-1 < s\cdot(2n-1)+s = 2ns \le n2^{n+1} </tex>. | ::<tex> size_{B}(f)\le s\cdot(2n-1)+s-1 < s\cdot(2n-1)+s = 2ns \le n2^{n+1} </tex>. | ||
| − | |||
| − | |||
Таким образом, для любой функции <tex> f(x_{1},...,x_{n}) </tex> выполняется неравенство | Таким образом, для любой функции <tex> f(x_{1},...,x_{n}) </tex> выполняется неравенство | ||
| Строка 58: | Строка 60: | ||
{{Определение | {{Определение | ||
| − | |definition= <tex> f(n) \sim g(n) </tex> означает, что <tex>f</tex> асимптотически эквивалентна <tex>g</tex>, то есть <tex>\ | + | |definition= <tex> f(n) \sim g(n) </tex> означает, что <tex>f</tex> асимптотически эквивалентна <tex>g</tex>, то есть <tex>\lim\limits_{n \to \infty}\frac{f(n)}{g(n)} = 1</tex> |
}} | }} | ||
{{Определение | {{Определение | ||
| − | |definition= <tex> f(n) \lesssim g(n) </tex> означает, что <tex>\ | + | |definition= <tex> f(n) \lesssim g(n) </tex> означает, что <tex>\varlimsup\limits_{n \to \infty}\frac{f(n)}{g(n)} \le 1</tex> |
}} | }} | ||
| Строка 79: | Строка 81: | ||
::<tex> size_{B}(K_{n}) \le size_{B}(K_{k}) + size_{B}(K_{n-k}) + 2^n </tex>. | ::<tex> size_{B}(K_{n}) \le size_{B}(K_{k}) + size_{B}(K_{n-k}) + 2^n </tex>. | ||
| − | Так как по [[#Th1| | + | Так как по [[#Th1|теореме 1]] <tex> size_{B}(K_{k}) \le k2^{k+1} </tex> , <tex> size_{B}(K_{n-k}) \le (n-k)2^{n-k+1} </tex>,то |
::<tex> size_{B}(K_{n}) \le k2^{k+1} + (n-k)2^{n-k+1} + 2^n </tex>. | ::<tex> size_{B}(K_{n}) \le k2^{k+1} + (n-k)2^{n-k+1} + 2^n </tex>. | ||
| Строка 117: | Строка 119: | ||
|statement =Для любой функции <tex> f(x_{1}, ..., x_{n}) </tex> имеет место соотношение <tex> size_{B}(f)\lesssim 12\frac {2^{n}}{n} </tex>. | |statement =Для любой функции <tex> f(x_{1}, ..., x_{n}) </tex> имеет место соотношение <tex> size_{B}(f)\lesssim 12\frac {2^{n}}{n} </tex>. | ||
|proof = [[Файл:Synschemes-Theorem2.png|300px|thumb|right|Рис. 4]] | |proof = [[Файл:Synschemes-Theorem2.png|300px|thumb|right|Рис. 4]] | ||
| − | Пусть <tex> f(x_{1},...,x_{n}) </tex> {{---}} произвольная булева функция. Рассмотрим разложение <tex> f </tex> по переменным <tex> x_{1},...,x_{ | + | Пусть <tex> f(x_{1},...,x_{n}) </tex> {{---}} произвольная булева функция. Рассмотрим разложение <tex> f </tex> по переменным <tex> x_{1},...,x_{m} </tex>, где <tex> 1 \le m \le n </tex>: |
| + | |||
| + | Введем функцию | ||
| + | |||
| + | <tex> x^{\sigma} = \begin{cases} | ||
| + | x, \sigma =1;\\ | ||
| + | \overline{x}, \sigma =0 | ||
| + | \end{cases}</tex> | ||
| + | |||
| + | Тогда | ||
| − | <tex> f(x_{1},...,x_{n})= \ | + | <tex>f(x_{1},...,x_{n})=\displaystyle\bigvee_{(\sigma_{1},\dotsc,\sigma_{m})}x_{1}^{\sigma_{1}}\wedge\dotsc\wedge x_{m}^{\sigma_{m}}\wedge f(\sigma_{1},\dotsc,\sigma_{m},x_{m+1},\dotsc,x_{n}) </tex>. (Дизъюнкция берется по всевозможным наборам значений переменных <tex> (x_{1},\dotsc,x_{m}) </tex>. |
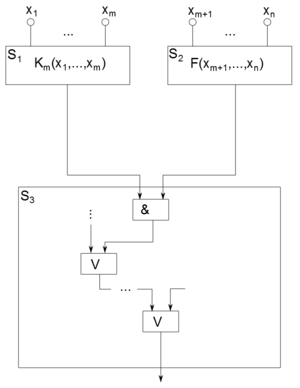
| − | Схема для функции <tex> f </tex> строится из трех подсхем: <tex> S_{1},S_{2},S_{3} </tex>. (рис. 4) | + | '''Схема для функции <tex> f </tex> строится из трех подсхем: <tex> S_{1},S_{2},S_{3} </tex>. (рис. 4)''' |
| − | :1. Схема <tex> S_{1} </tex> реализует все конъюнкции из множества <tex> K_{m} (x_{1},...,x_{m}) </tex>. В силу [[#Lemma2| | + | :1. Схема <tex> S_{1} </tex> реализует все конъюнкции из множества <tex> K_{m} (x_{1},...,x_{m}) </tex>. В силу [[#Lemma2|леммы 2]] выполняется неравенство |
::<tex> size_{B}(S_{1}) \le size_{B}(K_{m}) \lesssim 2^{m} </tex>. | ::<tex> size_{B}(S_{1}) \le size_{B}(K_{m}) \lesssim 2^{m} </tex>. | ||
| − | :2. Схема <tex> S_{2} </tex> реализует систему <tex> F(x_{m+1},...,x_{n}) </tex> всех булевых функций от переменных <tex> x_{m+1},...,x_{n} </tex>. Другими словами, подсхема <tex> S_{2} </tex> вычисляет все булевы функции, зависящие от последних <tex> n - m </tex> переменных. В силу [[#Th1| | + | :2. Схема <tex> S_{2} </tex> реализует систему <tex> F(x_{m+1},...,x_{n}) </tex> всех булевых функций от переменных <tex> x_{m+1},...,x_{n} </tex>. Другими словами, подсхема <tex> S_{2} </tex> вычисляет все булевы функции, зависящие от последних <tex> n - m </tex> переменных. В силу [[#Th1|теоремы 1]] |
::<tex> size_{B}(S_{2}) \le (n-m)2^{n-m+1}2^{2^{n-m}} </tex>. | ::<tex> size_{B}(S_{2}) \le (n-m)2^{n-m+1}2^{2^{n-m}} </tex>. | ||
Версия 23:54, 17 ноября 2013
| Определение: |
| Синтезом схемы из функциональных элементов называется процедура получения логической схемы, реализующей заданную логическую функцию. |
Приведем несколько простейших алгоритмов синтеза схем, реализующих произвольную функцию от аргументов , в случае когда базис .
Содержание
Метод синтеза, основанный на совершенной ДНФ
| Лемма (1): |
Для любой функции , реализующей конъюнкцию аргументов, |
| Доказательство: |
|
Построим данную схему следующим образом: возьмем элементов отрицания, присоединенных к выходам, и цепочки из элементов конъюнкции, имеющих "свободных" входов. Если -й множитель равен , то -й вход этой цепочки присоединяется к входу схемы. А если -й множитель равен ,то присоединяется к выходу -го элемента отрицания.(рис. 1) Очевидно, что сложность построенной схемы . Поэтому . Лемма доказана. |
| Теорема (1): |
Для любой функции имеет место неравенство |
| Доказательство: |
|
Пусть — произвольная булева функция. Если , то схема строится в соответствии с представлением , то есть . Если , то может быть задана дизъюнктивной нормальной формой
где и каждая конъюнкция имеет вид Схема для состоит из конъюнкций (каждая из них в соответствии с леммой 1 имеет сложность не более ) и цепочки из элемента дизъюнкции с свободными входами. Свободные входы этой цепочки присоединяются к выходам схем для конъюнкций .(рис. 2) Имеем
Таким образом, для любой функции выполняется неравенство
Поэтому . Теорема доказана. |
Метод синтеза, основанный на более компактной реализации множества всех конъюнкций
| Определение: |
| означает, что асимптотически эквивалентна , то есть |
| Определение: |
| означает, что |
| Лемма (2): |
Для функции , реализующей конъюнкцию элементов, имеет место соотношение |
| Доказательство: |
|
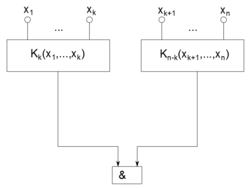
Разделим цепочки конъюнкций на две части. Каждая конъюнкция может быть представлена в виде конъюнкции двух конъюнкций длины и :
Поэтому схема для может быть образована из схем для и и системы из элементов конъюнкции, осуществляющих вышеприведенную операцию.(рис. 3) Следовательно,
Так как по теореме 1 , ,то
Положим . Тогда , и
С другой стороны, при каждая конъюнкция реализуется на выходе некоторого элемента, то есть при выполняется неравенство . Таким образом,
|
| Теорема (2): |
Для любой функции имеет место соотношение . |
| Доказательство: |
|
Пусть — произвольная булева функция, . Заменим в схеме (рис. 2) верхнюю часть схемы, реализующую конъюнкции , схемой, реализующей все конъюнкции из . Тогда для любой такой функции (не равной нулю) имеем Таким образом, |
Метод синтеза схем К.Э.Шеннона
| Теорема (3): |
Для любой функции имеет место соотношение . |
| Доказательство: |
|
Пусть — произвольная булева функция. Рассмотрим разложение по переменным , где : Введем функцию
Тогда . (Дизъюнкция берется по всевозможным наборам значений переменных . Схема для функции строится из трех подсхем: . (рис. 4)
Поэтому выполняется неравенство . Таким образом,
Положим (для упрощения дальнейших выкладок) . Тогда
Заметим, что второе слагаемое "очень быстро" растет с ростом , а первое слагаемое убывает с ростом медленней. Поэтому следует взять такое значение , при котором первое и второе слагаемые приблизительно равны, и потом немного уменьшить . Тогда второе слагаемое "сильно" уменьшится, а первое "не очень сильно" возрастет. Возьмем, например, . Тогда
то есть получили "слишком много". Возьмем на единицу меньше: . Тогда
Вспомним теперь, что должно быть целым числом, и положим . Тогда ,
При этом выборе окончательно имеем
|
Литература
- Яблонский С.В. Введение в дискретную математику. — 4-е изд. — М.: Высшая школа, 2003. — 384 с. — ISBN 5-06-004681-8