Участник:AntonM3135
| Определение: |
| Числа Фибоначчи -- числовая последовательность первые два члена которой равны 0 и 1, либо 1 и 1, а каждый последующий равен сумме двух предыдущих |
$F_1=1, F_2=1, F_n=F_{n-1} + F_{n-2}$,
где $n>=2$
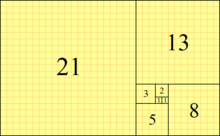
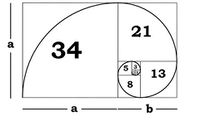
пример: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …
также числа Фибоначчи можно обобщить на произвольные начальные значения $F_1$ и $F_2$ например Числа Люка
Содержание
Числа Фибоначчи и золотое сечение
Золотое сечение может быть выражено, с помощью чисел Фибоначчи: $$\Phi=\lim\limits_{x \to \infty} \dfrac{F_{n+1}}{F_n}$$
Формула Бине
Формула $Бине$ выражает в явном виде значение $F_{n}$ как функцию от $n$:
$F_n=\dfrac{\phi^n - (-\phi)^{-n}}{2\phi - 1}$,где
$\phi=\dfrac{\sqrt5 + 1}{2}$ - золотое сечение
Доказательство
- $\psi=\dfrac{1-\sqrt{5}}{2}=-\dfrac{1}{\phi}$
Докажем формулу по индукции. Для этого нужно доказать равенство $\phi^n - \psi^n + \phi^{n+1} - \psi^{n+1}= \psi^{n+2} - \phi^{n+2}$, которое после преобразования превращается в $\phi^n(1 - \phi - \phi^2) = \psi^n(1 - \psi - \psi^2)$. Осталось заметить, что оба числа, $\phi$ и $\psi$, служат корнями многочлена $1 - a - a^2$, так что выражения в скобках в обеих частях равенства обращаются в ноль одновременно. Вот и доказан индуктивный переход. Что же касается базы индукции, то она совершенно очевидна при n=0 и n=1.
Тождества
| Теорема: |
$\displaystyle\sum_{i=1}^{n} F_i=F_{n+2} - 1$ |
| Доказательство: |
|
Будем доказывать по индукции
База
Шаг индукции предположи что для $n$ верно
Тогда нужно доказать для $n+1$
упрощая получается
|
| Теорема: |
$\displaystyle F_{1}+F_{3}+F_{5}+\dots +F_{2n-1}=F_{2n}$ |
| Теорема: |
$\displaystyle F_{2}+F_{4}+F_{6}+\dots +F_{2n}=F_{2n+1}-1$ |
| Теорема: |
$\displaystyle\sum_{i=1}^{2n -1} F_i^2=F_{n}F_{n+1}$ |
| Теорема: |
$F_n^2 + F_{n+1}^2=F_{2n+1}$ |
| Теорема: |
$\displaystyle F_{2n}=F_{n+1}^{2}-F_{n-1}^{2}$ |
| Теорема: |
$\displaystyle F_{3n}=F_{n+1}^{3}+F_{n}^{3}-F_{n-1}^{3}$ |
| Теорема: |
$\displaystyle F_{5n}=25F_{n}^{5}+25(-1)^{n}F_{n}^{3}+5F_{n}$ |
| Теорема: |
$\displaystyle F_{n+1}=\sum_{i=0}^{n} \binom{n-1}{i}$ |
- Из этой формулы следует, что сумма биномиальный коэффициентов на диагонали
треугольника паскаля есть число Фибоначчи
Фибоначева Система счисления
Фибоначчива Система счисления - позиционная система счисления для целых чисел на основе чисел Фибоначчи.
Представление натуральных чисел
| Теорема: | ||||||
Любое неотрицательное целое число $\displaystyle a$ можно единственным образом представить последовательностью битов $…ε_k…ε_4ε_3ε_2$ $\varepsilon _{k}\in \{0,1\}$ так, что $\displaystyle a=\sum _{k}\varepsilon _{k}F_{k}$, причём последовательность ${ε_k}$ содержит лишь конечное число единиц, и не имеет пар соседних единиц:$\displaystyle \forall k\geq 2\colon (\varepsilon _{k}=1)\Rightarrow (\varepsilon _{k+1}=0)$. | ||||||
| Доказательство: | ||||||
|
Докажем существование представления
Докажем единственность представления
Теперь возьмем два непустых множества из различных непоследовательных чисел Фибоначчи S и T с одной и той же суммой элементов. Рассмотрим множества S′ и T′, равные S и T, из которых удалены общие элементы (т. е. S′ = S \ T и T′ = T \ S). Поскольку S и T имеют одну и ту же сумму элементов, и из них удалены одни и те же элементы (а именно элементы из S ∩ T), S′ и T′ также должны иметь одну и ту же сумму элементов. Докажем от противного, что хотя бы одно из множеств S′ и T′ пусто. Предположим, что это не так, т. е. что S′ и T′ оба непусты, и пусть наибольший элемент S′ есть $F_s$, а наибольший элемент T′ есть $F_t$. Поскольку S′ и T′ не содержат общих элементов, $F_s ≠ F_t$. Без потери общности предположим, что $F_s < F_t$. Тогда по лемме сумма элементов S′ строго меньше, чем $F_{s+1}$, т. е. строго меньше, чем $F_t$, поскольку сумма элементов T′ не меньше, чем $F_t$. А это противоречит тому, что S′ и T′ имеют одинаковую сумму элементов. Следовательно, либо S′, либо T′ пусто. Пусть (без потери общности) пусто S′. Тогда сумма элементов S′ равна нулю, значит, сумма элементов T′ также равна нулю, значит, T′ — также пустое множество (оно содержит только натуральные числа). Значит, S′ = T′ = ∅, т. е. S = T, что и требовалось доказать. | ||||||
Наихудший случай алгоритма Евклида
Если для алгоритма Евклида требуются N шагов для пары натуральных чисел $a > b > 0$, наименьшие значения a и b, для которых это выполняется — числа Фибоначчи $F_{N+2}$ и $F_{N+1}$ соответственно. Тогда, если алгоритм Евклида требует N шагов для пары чисел $(a,b)$, где $a > b$, выполняются следующие неравенства $a ≥ F_{N+2}$ и $b ≥ F_{N+1}$. Доказать это можно по математической индукции. Если N = 1, тогда a делится на b без остатка. Наименьшие натуральные числа, для которых это верно, равны b = 1 и a = 2, соответственно F2 и F3. Предположим теперь, что результат выполняется для всех значений N до M − 1. Первый шаг алгоритма Евклида с M шагами $a = q_0b + r_0$, и алгоритм Евклида для пары чисел $(b,r_0)$, где b > r0, требует M − 1 шагов. По предположению индукции имеем $b ≥ F_{M+1}$ и $r_0 >= F_M$. Следовательно, $a = q_0b + r_0 ≥ b + r_0 ≥ F_{M+1} + F_M = F_{M+2}$, что является искомым неравенством. Это доказательство, опубликованное Габриэлем Ламе в 1844 году