Формула включения-исключения — различия между версиями
GR1n (обсуждение | вклад) (→Формула включения-исключения) |
GR1n (обсуждение | вклад) (→Формула включения-исключения) |
||
| Строка 49: | Строка 49: | ||
Тогда | Тогда | ||
| − | <tex> | A |=| A_n |+\Bigg( \sum \limits_{I_{n-1}} (-1)^{|I_{n-1}|+1} \Big| \bigcap \limits_{ j \in I_{n-1} } A_j \Big| \Bigg) + \Bigg( \sum \limits_{I_{n-1}} (-1)^{|I_{n-1}|+2} \Big| \bigcap \limits_{ j\in I_{n-1} \cup \{ n \} } A_j \Big| \Bigg) = \sum \limits_{I_n} (-1)^{|I_n|+1} \Big| \bigcap \limits_{ j \in I_n } A_j \Big| )</tex> | + | <tex> | A |=| A_n |+\Bigg( \sum \limits_{I_{n-1}} (-1)^{|I_{n-1}|+1} \Big| \bigcap \limits_{ j \in I_{n-1} } A_j \Big| \Bigg) + \Bigg( \sum \limits_{I_{n-1}} (-1)^{|I_{n-1}|+2} \Big| \bigcap \limits_{ j\in I_{n-1} \cup \{ n \} } A_j \Big| \Bigg) = \sum \limits_{I_n} (-1)^{|I_n|+1} \Big| \bigcap \limits_{ j \in I_n } A_j \Big| )</tex> . |
| + | Равенство справедливо, потому что все наборы <tex> I_n </tex> можно разбить на три группы : | ||
| + | |||
| + | 1) <tex> (n) </tex> | ||
| + | |||
| + | 2) <tex> (I_{n-1})</tex> Это означает, что в наборе точно '''не''' будет присутствовать индекс <tex> n </tex>, а будут все различные варианты индексов остальных множеств, т.е. <tex> I_{n-1} </tex> | ||
| + | |||
| + | 3) <tex> (n; I_{n-1}) </tex> Аналогично предыдущему, только в наборе будет индекс <tex> n </tex> | ||
| + | |||
| + | Как видно из равенства, каждое слагаемое "отвечает" за соответствующие группы. Значит равенство истинно. | ||
Значит для <tex>~l=n</tex> мы доказали, что равенство верно. Значит индукционный переход доказан, то теорема доказана. | Значит для <tex>~l=n</tex> мы доказали, что равенство верно. Значит индукционный переход доказан, то теорема доказана. | ||
}} | }} | ||
Версия 04:16, 19 октября 2011
Формула включения-исключения
Формула включения-исключения - это комбинаторная формула, которая позволяет определить мощность объединения конечных множеств, если известны их мощности и мощности всех их возможных пересечений.
Например, в случае двух множеств формула включения-исключения имеет вид:
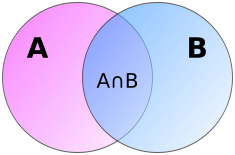
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
| Теорема: |
Пусть , тогда по формуле включения-исключения: |
| Доказательство: |
|
Будем доказывать теорему, опираясь на метод математической индукции. Пусть — это количество множеств, мощность пересечения которых мы ищем. Для случая и теорема, очевидно, верна. Таким образом, — база индукции. Предположим, что для теорема верна, то есть равенство выполняется. Докажем, что равенство истинно для
Заметим, что Тогда . Равенство справедливо, потому что все наборы можно разбить на три группы : 1) 2) Это означает, что в наборе точно не будет присутствовать индекс , а будут все различные варианты индексов остальных множеств, т.е. 3) Аналогично предыдущему, только в наборе будет индекс Как видно из равенства, каждое слагаемое "отвечает" за соответствующие группы. Значит равенство истинно. Значит для мы доказали, что равенство верно. Значит индукционный переход доказан, то теорема доказана. |