Формула включения-исключения — различия между версиями
GR1n (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
| − | '''Формула | + | '''Формула включения–исключения''' {{---}} это комбинаторная формула, которая позволяет определить мощность объединения конечных множеств, если известны их мощности и мощности всех их возможных пересечений. |
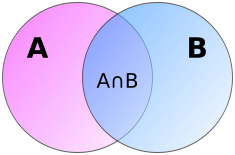
[[Файл:пересечение двух множеств.svg.png|thumb|right|Случай для двух множеств]] | [[Файл:пересечение двух множеств.svg.png|thumb|right|Случай для двух множеств]] | ||
| Строка 7: | Строка 7: | ||
<tex> | A \cup B | = | A | + | B | - | A \cap B |</tex> | <tex> | A \cup B | = | A | + | B | - | A \cap B |</tex> | ||
</center> | </center> | ||
| − | В сумме <tex>~| A | + | B |</tex> элементы пересечения <tex>A \cap B</tex> учтены дважды, и, чтобы компенсировать это, мы вычитаем <tex> | A \cap B |</tex> из правой части формулы. Справедливость этого рассуждения видна из диаграммы | + | В сумме <tex>~| A | + | B |</tex> элементы пересечения <tex>A \cap B</tex> учтены дважды, и, чтобы компенсировать это, мы вычитаем <tex> | A \cap B |</tex> из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера–Венна для двух множеств, приведенной на рисунке справа. |
Таким же образом и в случае <tex>~n>2</tex> множеств процесс нахождения количества элементов объединения <tex>A_1 \cup A_2 \cup \ldots \cup A_n</tex> состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы. | Таким же образом и в случае <tex>~n>2</tex> множеств процесс нахождения количества элементов объединения <tex>A_1 \cup A_2 \cup \ldots \cup A_n</tex> состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы. | ||
{{Теорема | {{Теорема | ||
| − | |statement=Пусть <tex> A = \bigcup \limits_{i=1}^{n}A_i </tex> , тогда по формуле | + | |statement=Пусть <tex> A = \bigcup \limits_{i=1}^{n}A_i </tex> , тогда по формуле включения–исключения: <center> <tex> | A | = \sum \limits_{I \in 2^N} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| </tex> </center> |
Причем <tex> N = \{ 1,2, \ldots ,n \} </tex>, <tex> I </tex> {{---}} подмножество множества <tex> 2^N </tex>(Прим. для множества <tex> X </tex> запись <tex> 2^X </tex> означает множество всех подмножеств <tex> X </tex>). За <tex> j </tex> примем индекс текущего множества (причем <tex> j \in I </tex>), которое будет входить в пересечение в текущем слагаемом. | Причем <tex> N = \{ 1,2, \ldots ,n \} </tex>, <tex> I </tex> {{---}} подмножество множества <tex> 2^N </tex>(Прим. для множества <tex> X </tex> запись <tex> 2^X </tex> означает множество всех подмножеств <tex> X </tex>). За <tex> j </tex> примем индекс текущего множества (причем <tex> j \in I </tex>), которое будет входить в пересечение в текущем слагаемом. | ||
| Строка 24: | Строка 24: | ||
| − | Пусть | + | Пусть <tex> A </tex> {{---}} пересечение <tex>~n</tex> множеств. Тогда очевидно, что <tex> A = \bigcup \limits_{i=1}^{n}A_i = \left( {\bigcup \limits_{i=1}^{n-1}A_i} \right) \cup A_n </tex>. Пусть <tex> B = \bigcup \limits_{i=1}^{n-1}A_i </tex>; <tex>N_{-1} = \{ 1,2, \ldots ,n-1 \} </tex>. |
| − | Тогда исходя из предположения индукции имеем, что | + | Тогда, исходя из предположения индукции, имеем, что |
<tex> | B | = \sum \limits_{I \in 2^{N_{-1}}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| </tex> | <tex> | B | = \sum \limits_{I \in 2^{N_{-1}}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| </tex> | ||
| Строка 55: | Строка 55: | ||
# <tex> \{ n \} </tex> | # <tex> \{ n \} </tex> | ||
| − | # <tex> I \in 2^{ | + | # <tex> I \in 2^{N\setminus \{n\}} </tex> Это означает, что в наборе точно '''не''' будет присутствовать индекс <tex> n </tex>, а будут все различные варианты индексов остальных множеств, т.е. <tex> I \in 2^{N\setminus \{n\}}</tex> |
| − | # <tex> \{ n \} \cup I \in 2^{ | + | # <tex> \{ n \} \cup I \in 2^{N\setminus \{n\}} </tex> Аналогично предыдущему, только в наборе будет индекс <tex> n </tex> |
| − | Как видно из равенства, каждое слагаемое "отвечает" за соответствующие группы. Значит равенство истинно. | + | Как видно из равенства, каждое слагаемое "отвечает" за соответствующие группы. Значит, равенство истинно. |
| − | + | Таким образом, для <tex>~l=n</tex> мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана. | |
}} | }} | ||
Версия 22:47, 19 октября 2011
Формула включения–исключения — это комбинаторная формула, которая позволяет определить мощность объединения конечных множеств, если известны их мощности и мощности всех их возможных пересечений.
Например, в случае двух множеств формула включения—исключения имеет вид:
В сумме элементы пересечения учтены дважды, и, чтобы компенсировать это, мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера–Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
| Теорема: |
Пусть , тогда по формуле включения–исключения: |
| Доказательство: |
|
Доказываем теорему по индукции. Пусть — это количество множеств, мощность пересечения которых мы ищем. Для случая и теорема, очевидно, верна. Таким образом, — база индукции. Предположим, что для равенство верно. Докажем, что равенство истинно для
В силу того, что Имеем в предыдущей формуле . Равенство справедливо, потому что все наборы можно разбить на три группы :
Как видно из равенства, каждое слагаемое "отвечает" за соответствующие группы. Значит, равенство истинно. Таким образом, для мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана. |