Straight skeleton

Существует целый класс структур типа [math]\mathrm{skeleton}[/math], которые описывают базовые топологические свойства объектов. Структура была придумала Oswin Aichholzer. Она используются в различных практических задачах (проектирование крыш для зданий) и для доказательства некоторых теорем^[1].

Топологические свойства

Определение:

Straight skeleton (Angular Bisector Network, ABN) полигона без самопересечений называется планарный граф, определяющий разбиение полигона на регионы, границами которых являются стороны полигона, биссектрисы углов и отрезки, соединяющие вершины straight skeleton, образовавшиеся в результате сжатия полигона.

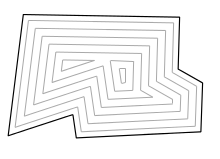
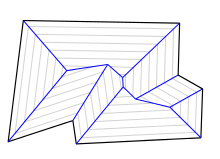
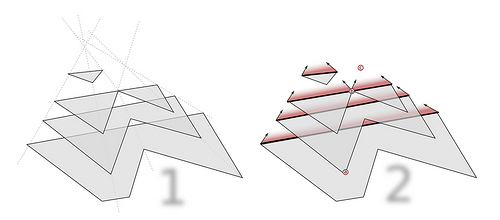
Опишем подробней, как получается такое разбиение. Мы можем представить, будто все стороны прямоугольника параллельно двигаются внутрь с одинаковой постоянной скоростью, то есть многоугольник как бы сжимается внутрь. Тогда вершины будут двигаться вдоль биссектрис , а точки пересечения биссектрис будут являться точками, в которых рёбра полностью сократились (выродились в точку). В каждый момент времени от начала движения рёбер мы получаем слоистую структуру (рис 1.). На рис. 2 синим цветом выделен — множество отрезков, образованных точками пересечения при движении сторон полигона. Чем-то структура похожа на строение крыши в домах (рис. 3). И для решения этой задачи как раз и может применяться: по стенам здания необходимо спроектировать его крышу.

Рис. 1 — слои в разные моменты времени

Рис. 2 — дерево

Рис. 3 — пример крыши по

Проектирование крыши здания по готовым стенам

Процесса стягивания многоугольника продолжается до тех пор, пока происходят его топологические изменения, то есть меняется число вершин в стянутом многоугольнике, и таким образом появляются новые вершины дерева . Существуют два типа изменений, в ходе которых образуются новые вершины дерева:

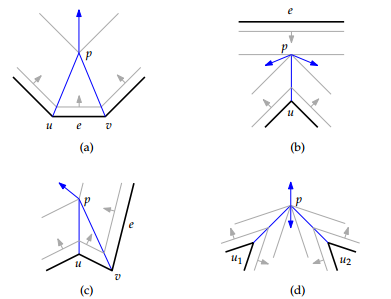
[math] Edge\ event [/math] — данное изменение происходит, когда сторона многоугольника полностью стягивается, делая соседние стороны инцидентными.
[math] Split\ event [/math] — происходит, когда ребро разбивается на два новых ребра, исходящих из точки преломления старого. Такое событие происходит на биссектрисе вогнутой вершины многоугольника. И тогда стягиваемая многоугольником область может разбивться на две непересекающиеся многоугольные области.

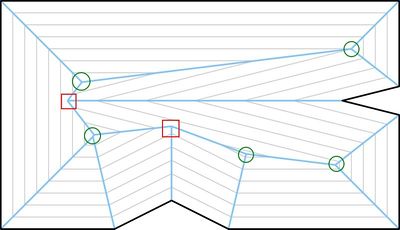
На рисунке [math]edge\ event'[/math]ы изображены зелёным кругом, а [math]split\ event'[/math]ы — красным прямоугольником.

Таким образом, [math] event' [/math]ы соответствуют внутренним вершинам , гранями являются области многоугольника, заметаемые сторонами многоугольника в процессе стягивания, дуги соединяют либо две внутренние вершины либо внутреннюю вершину с листом — вершиной многоугольника.

Стоит также отметить, что в общем случае [math] split\ event'[/math]ы могут быть нетривиальными. На рисунке ниже в случае [math] (c) [/math] в вершине [math] p [/math] совпали [math]split\ event[/math] из вершины [math] u [/math] и ребра [math] e [/math] и [math] edge\ event[/math] ребра [math] uv [/math], а в случае [math] (d) [/math] совпали два [math] split\ event'[/math]а вершин [math] u_1 [/math] и [math] u_2 [/math]. Случаи [math] (a) [/math] и [math] (b) [/math] — простые [math] edge [/math] и [math] split\ event'[/math]ы.

Задача построения такого является частным случаем задачи построения , где каждому ребру можно задавать вес, то есть скорость движения ребра. И эта скорость может быть даже отрицательной. Таким образом можно оффсетить полигоны и решать задачу motion planning. Задача является более сложной, и здесь рассматриваться не будет.

Свойства Straight skeleton

Из процесса построения следует, что он является планарным графом. Ранее уже упоминалось, что он также является деревом. Будем обозначать простого полигона без самопересечений [math] P [/math], в котором [math] n [/math] вершин, как [math] S(P) [/math]. Тогда справедливы следующие леммы:

Лемма (1):

является деревом, содержит граней, не более внутренние вершины и не более рёбер.

Доказательство:

Каждая грань [math] f(e) [/math] начинает образовываться во время стягивания ребра [math] e [/math], и даже если на ребре произошёл [math] split\ event [/math], сама грань не могла разделиться. Построение грани [math] f(e) [/math] завершается, когда ребро [math] e [/math] полностью стягивается. И это ребро дальше не может появиться снова, поэтому граней в [math] S(P) [/math] столько, сколько сторон в многоугольнике, то есть ровно [math] n [/math].

То, что [math] S(P) [/math] является деревом, легко доказывается по индукции. База верна, когда внутренняя вершина всего одна. Тогда у листьями будут вершины многоугольника. Такой граф очевидным образом будет деревом. Если в внутренних вершин, то рассмотрим самый первый [math] edge\ event[/math]. Он закончился в какой-то внутренней вершине , у неё есть смежные листья — вершины, инцидентные этому ребру, — и из неё достижимы другие ы, с не более чем [math] k - 1 [/math] внутренними вершинами, и они являются деревьями по предположению индукцию. Тогда получаем, что [math] S(P) [/math] для [math] k [/math] вершин тоже будет деревом.

Внутренние вершины в имеют степень не меньше — простой перебор всех случаев ов (степень будет больше, если в одной вершине совпало несколько событий). Так как имеет листьев, то внутренних вершин будет не больше , а так как является деревом, то рёбер у него будет не более .

Замечание: если мы рассмотрим в какой-то момент времени, то он вполне может содержать циклы (это видно на рисунке ниже). Однако его конечная структура будет деревом.

Алгоритм с изпользованием SLAV

Далее будет описан алгоритм, придуманный Petr Felkel, который строит за время , или просто [math] \mathcal{O}(n^2)[/math], где [math] n [/math] — общее число вершин в полигоне, [math] m [/math] — число вогнутых вершин в полигоне. Немного модифицированный этот алгоритм используется в открытой библиотеке вычислительной геометрии CGAL^[2]. Однако этот алгоритм всё равно ещё достаточно медленный. В реальной жизни используют его модификации или более сложные алгоритмы.

Сначала алгоритм будет рассмотрен на простом случае — выпуклом многоугольнике, — а потом на невыпуклом многоугольнике.

Выпуклый полигон

В случае выпуклого многоугольника возникают только [math] edge\ event'[/math]ы по определению. Поэтому просто алгоритм можно описать следующим образом: найдём точки пересечения биссектрис многоугольника для каждой вершины со всеми соседними вершинами, возьмём такую точку, в которой произойдёт самый первый [math] edge\ event[/math], добавим полученную вершину в , соеденим её с вершинами ребра, которое исчезло в процессе текущего [math] edge\ event'[/math]а, а потом перестроим полигон, создав новую вершину и подвинув все остальные вдоль биссектрис на одинаковое расстояние. Будем продолжать этот процесс до тех пор, пока многоугольник не превратится в треугольник.

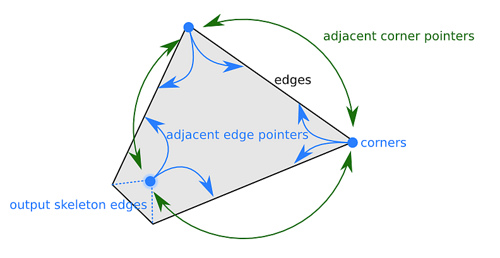
Теперь реализуем этот алгоритм более эффективно. Для этого мы будем использовать специальную структуру данных — [math] \mathrm{SLAV}[/math] (set of circular lists of active vertices). Эта структура хранит цикл всех вершин для внешней грани, а так же цикл для каждой дыры многоугольника и для всех многоугольников, возникающих в процессе построения [math] S(P) [/math]. В данном случае у нас будет просто [math] \mathrm{LAV}[/math] — циклический список всех вершин многоугольника.

В таком списке частично найденного вершины имеют указатели на следующую и предыдущую вершину в порядке обхода контура, а так же указатели на инцидентные рёбра. Если представить процесс стягивания многоугольника, как будто у нас уже построена для него крыша, а мы двигаем вверх некоторую заметающую плоскость, где пересечение крыши и плоскости будет обозначать текущий слой, то можно заметить, что область полигона разбивается на несколько частей. Каждой части будет соответствовать свой [math] \mathrm{LAV}[/math], отсюда нам и нужен [math] \mathrm{SLAV}[/math].

Алгоритм для выпуклых полигонов

Далее считаем, что полигон представлен рёбрами вдоль движения по контуру полигона против часовой стрелки.

Шаг 1. Инициализация:

Поместим все вершины многоугольника в двусвязный циклический список в порядке обхода вдоль контура. Все вершины в считаются активными сейчас.

Для каждой вершины в добавим указатели на инцидентные рёбра и , а также найдём луч биссектрисы .

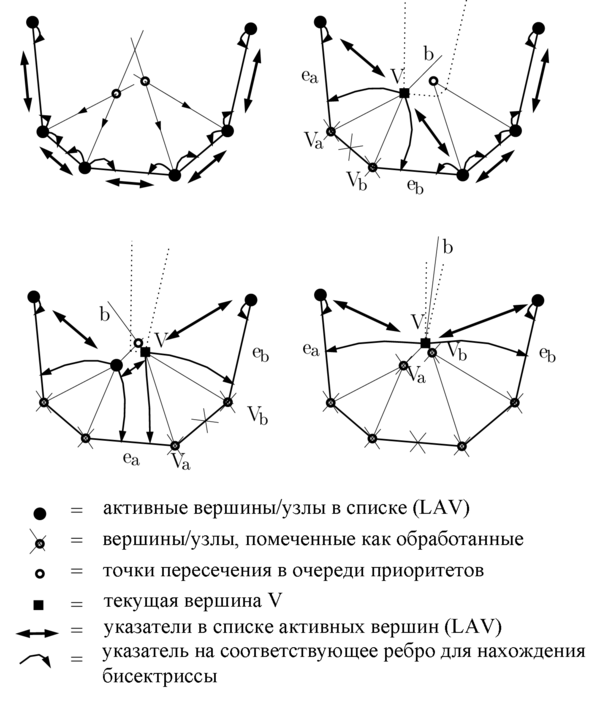
Для каждой вершины найдём ближайшее пересечение биссектрисы с лучами и . Если это пересечение существует, то положим его в приоритетную очередь согласно — расстоянию от точки пересечения до одного из рёбер, инцидентных вершине . Для каждой точки пересечения будем так же хранить два указателя на вершины и — начала лучей биссектрис, которые пересекаются в точке . Эти указатели понадобятся в будущем, когда нужно будет определять соответствующие вершинам рёбра (см. рисунок ниже).

Шаг 2. Следующие действия выполняются в цикле, пока приоритетная очередь не пустая:

Извлечём точку пересечения из приоритетной очереди.

Если вершины и , соответствующие данной точке пересечения помечены как обработанные, то переходим к следующей итерации цикла шага 2. Это означает, что ребро между данными вершинами полностью стянулось (обработанные вершины и стянутые рёбра помечены крестом на рисунке ниже).

Если осталось всего три вершины , то добавим в рёбра . В случае выпуклого многоугольника в этом месте можно завершить алгоритм. Но в общем случае нужно будет перейти к началу цикла снова.

Добавим в рёбра .

Теперь необходимо модифицировать (детали на рисунке ниже):

пометим вершины [math] V_a [/math] и [math] V_b [/math] как обработанные (напомню, что они обозначаются крестом на рисунке к данному алгоритму),
создадим новую вершину [math] V [/math] в точке пересечения [math] I [/math] (отмечена квадратиком на рисунке),
добавим вершину [math] V [/math] в [math] \mathrm{LAV}[/math], то есть между предыдущем к [math] V_a [/math] и следующим к [math] V_b [/math] узлами,
добавим вершине [math] V [/math] указатели на соответствующие рёбра [math] e_a [/math] и [math] e_b [/math].

Посчитаем дополнительные величины для вершины :

луч биссектрисы [math] b [/math] между рёбрами [math] e_a [/math] и [math] e_b [/math],
точки пересечения луча b с соседями [math] V [/math] в [math] \mathrm{LAV}[/math], как в шаге [math] 1c [/math]
сохраним ближайшие точки пересечения в приоритетной очереди.

Заметим, что нам не нужно пересчитывать все расстояния в очереди приоритетов. Если мы стянем полигон до первого события исчезания ребра, то относительный порядок остальных событий не изменится. Нам необходимо только вставить новые точки пересечения в правильные места. Это можно эффективно сделать, если использовать структуру данных типа skip list.

В этом случае асимптотика алгоритма составляет [math] \mathcal{O}(n \log n)[/math], так как на каждой итерации цикла нам нужно положить константное число элементов в очередь, а итераций цикла не больше [math] n [/math].

Частные случаи

Частным случаем в алгоритме может быть совпадение нескольких [math] edge\ event'[/math]ов в одной точке. Эти совпадения добавляются в шагах [math] 1c [/math] и [math] 2f [/math], но могут быть относительно легко обработаны в шаге [math] 2b [/math].

Также может случиться, что какие-то рёбра не стянулись в итоге в одну вершину, а слились. Такое возможно, если какие-то стороны полигона были изначально параллельны (этот случай легко увидеть на прямоугольнике, не являющемся квадратом). С этим частным случаем можно разобраться в шаге [math] 2c [/math], проверив, не совпала ли одна из трёх вершин с другой. В выпуклом многоугольнике слияние двух рёбер может произойти только один раз (что неправда для невыпуклого многоугольника), поэтому здесь несложно разобраться с таким случаем.

Невыпуклый полигон

Основной принцип для невыпуклых полигонов такой же. Только с вершиной ещё хранится дополнительный атрибут, обозначающий событие, которое в ней произошло: [math] edge\ event[/math] или [math] split\ event[/math].

Наличие невыпуклой вершины может привести (а может и не привести) к разделению внутренней области. Невыпуклая вершина может так же участвовать в обычном [math] edge\ event'[/math]е (точка [math] A [/math] на рисунке выше). В таком случае [math] edge\ event'[/math]ы обрабатываются так же, как и в алгоритме с выпуклым многоугольником.

Посмотрим теперь, что делать с точкой [math] B [/math], в которой возникает [math] split\ event[/math].

Нахождение координат точки B

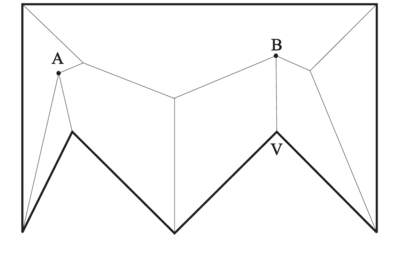
В простейшем случае точка [math] B [/math] появляется, когда "волновой фронт" распространения движения рёбер от невыпуклой вершины натыкается на встречный фронт противолежащего ребра. В такой момент возникает [math] split\ event[/math]. Поэтому точка [math] B [/math] может быть изначально охарактеризована, как точка, находящаяся на одном расстоянии от противолежащего угла и прямых, содержащих рёбра невыпуклой вершины. Задача состоит в том, чтобы найти это самое противолежащее ребро (случай [math] a) [/math] на рисунке выше). Но как показывает случай [math] b) [/math], простой тест на пересечение ребра и биссектрисы невыпуклой вершины не может быть использован (в этом случае луч биссектрисы пересекает сразу два ребра, непонятно, с каким из них произойдёт [math] split\ event[/math]). Поэтому необходимо ещё проверять, что точка [math] B [/math] лежит между лучами [math] b_i [/math] и [math] b_{i+1} [/math], идущих из вершин, инцидентных противолежащему ребру [math] e_i [/math].

Замечание: простой тест на пересечение биссектрисы вершины [math] V [/math] и целой линии, содержащей ребро, отсекает случаи тех рёбер, которые лежат позади вершины [math] V [/math].

Координаты возможной точки кандидата [math] B_i [/math] вычисляются следующим образом: это точка пересечения биссектрисы вершины [math] V [/math] и биссектрисы угла, который образуется в точке пересечения прямой, содержащей одно из рёбер, инцидентных [math] V [/math], и прямой, содержащей противолежащее ребро [math] e_i [/math]. Итоговая точка пересечения [math] B [/math] выбирается как ближайшая среди всех найденных точек [math] B_i [/math].

Частный случай: в этом месте также должна быть проверка на то, что противолежащее ребро не будет параллельно ни одному ребру вершины [math] V [/math]. Тогда рёбра могут накладываться друг на друга. TODO: И что делать?(

Работа с LAV в момент возникновения split event'a

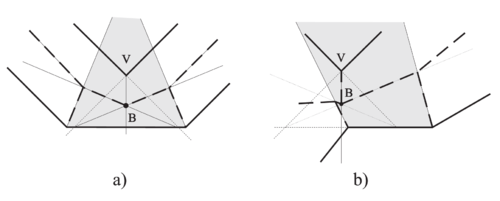
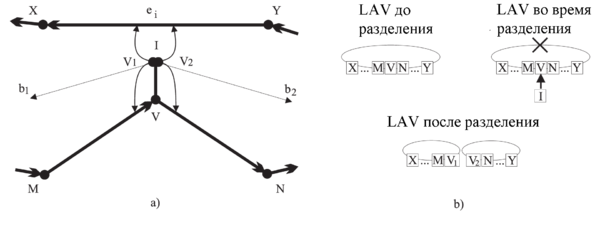
Когда происходит работа с точкой [math] B\ split\ event'[/math]а, то необходимо разбить соответствующий полигон на две части, что соответствует разделению [math] \mathrm{LAV} [/math] данного полигона на два списка. И в каждый новый список нужно вставить новую вершину [math] X [/math], образующуюся в точке пересечения [math] B [/math]. Обе вершины [math] X [/math] указывают на разделяющее ребро [math] e_i [/math] (см. рисунок выше).

Частный случай множественных split event'ов на одном ребре

Уже должно было стать понятно, что алгоритм не строит промежуточного представления , а работает исключительно с рёбрами исходного полигона. Это приводит к ситуации (см. рисунок выше), когда одно ребро является общим для нескольких новых полигонов в промежуточном представлении (то есть одно ребро меняет свою топологию несколько раз), образовавшихся после разделения старого полигона. В случае, когда ребро уже разбито, и происходит следующий за ним [math]event[/math], необходимо правильно определить концы противолежащего ребра (то есть вершины/узлы, которые активный в текущем уровне конструирования крыши, как например вершины [math] X [/math] и [math] Y [/math] на рисунке ниже).

Например, в данном случае ребро [math] SY [/math] является частью ребра [math] e_i = ZY [/math], которое стягивается и должно теперь указывать на вершину [math] X [/math]. Когда произойдёт следующее событые в точке пересечения [math] B [/math], то нам необходимо правильно указать ребро новой вершине в этой точке в [math] \mathrm{LAV} [/math]. Реальный конец ребра [math] e_i [/math] — точка [math] Z [/math], но мы хотим указать на ребро [math] XY [/math]. Это необходимо для поддержания корректности структуры [math] \mathrm{SLAV} [/math]. Ниже будет представлено два способа решения этой проблемы.

Первый способ

Можно физически разделить исходное ребро на два, вставив новую точку [math] S [/math]. Это решает проблему, так как никакое ребро не будет разделено дважды, а определение концов разделяемого ребра выполняется просто. Вставка вершины для точки [math] B [/math] в [math] \mathrm{LAV} [/math] тоже происходит относительно просто, потому что мы знаем точно, с каким ребром эта вершина связана. Но такой подход требует отдельно рассматривать вершины типа [math] S [/math], чтобы не добавить их случайно в .

Второй способ (используемый в авторском решении)

Идея заключается в том, чтобы хранить только вершины, которые реально будут в , а указатели на разделямое ребро хранятся во всех подполигонах, для которых это ребро является общим. Это приводит к множественным попаданиям [math] split\ event'[/math]ов на одно ребро.

Для примера, два полигона на рисунке выше разделяют общую ссылку на ребро [math] e_i [/math]. Во время процесса обработки вершины [math] B [/math] многоугольник [math] XMVNY [/math] разбивается на две части [math] XMB [/math] и [math] BNY [/math], а вершина [math] V [/math] помечается как обработанная.

Всё это нужно для того, чтобы правильно связать [math] B [/math] с вершинами [math] X [/math] и [math] Y [/math], а не с [math] Z [/math] и [math] Y [/math]. Во время обхода [math] \mathrm{SLAV} [/math] выбирается правильная часть ребра [math] e_i [/math] (в данном случае она определяется вершинами [math] X [/math] и [math] Y [/math]). Определяется следующим образом: вершина [math] B [/math] лежит справа от биссектрисы посещённой вершины [math] Y [/math] и слева от биссектрисы предка посещённой вершины [math] X [/math].

Алгоритм для невыпуклых полигонов

Шаг 1. Инициализация:

Положим все вершины в , как это делается в алгоритме для выпуклых многоугольников, а потом поместим в .

Найдём биссектрисы как в случае с выпуклым многоугольником.

Для каждой биссектрисы выпуклой вершины найдём ближайшую точку пересечения с биссектрисой соседней вершины, а для невыпуклых вершин найдём также точки пересечения с противолежащими рёбрами (как это описывалось раньше), и положим в приоритетную очередь ближайшую точку пересечения . Будем также с этой точкой хранить её тип — или .

Шаг 2. Пока очередь не пуста:

Извлечём точку пересечения из приоритетной очереди. Если она имеет тип , то её надо обработать так же, как в шагах алгоритма для невыпуклых полигонов. Иначе выполнять шаги ниже.

Если точка пересечения указывает на уже обработанные вершины, то продолжить со следующей итерации цикла шага 2, как в случае с выпуклым полигоном.

Нужно сделать примерно то же самое, что и шаге алгоритма для выпуклых многоугольников. Только на этом цикл не завершается, а продолжается с новой итерации, так как многоугольник мог разделиться на несколько частей, и, возможно, мы обработали лишь один подпалигон и не последний.

Добавим в ребро , где точка указывает на вершину . Для ов точки пересечения указывают ровно на одну вершину в .

Модифицируем теперь :

пометим вершину [math] V [/math] как обработанную,
создадим две новые вершины [math] V_1 [/math] и [math] V_2 [/math] с одинаковыми координатами точки пересечения [math] I [/math],
найдём для каждой вершины [math] V_1 [/math] и [math] V_2 [/math] противолежащее ребро в своём подпалигоне,
разделим [math] \mathrm{LAV}[/math] с вершиной [math] V [/math] на две части (как показано на рисунке выше), вставим в части вершины [math] V_1 [/math] и [math] V_2 [/math], а затем обе части добавим в [math] \mathrm{SLAV}[/math]. Вершина [math] V_1 [/math] будет следующей для предыдующего к [math] V [/math] узлу в [math] \mathrm{LAV}[/math] и предыдущей для конца противолежащего ребра. Аналогично для вершины [math] V_2 [/math]. Этот шаг в действительно разбивает полигон на две части,
Добавим указатели вершинам [math] V_1 [/math] и [math] V_2 [/math] на соответствующие рёбра.

Для обеих вершин и :

найдём биссектрисы между рёбрами, на которые эти вершины слинковались в шаге [math]2e[/math],
найдём точки пересечения лучей с биссектрисами соседних вершин как в шаге [math] 1c [/math] (тут могут получиться точки пересечения обоих типов),
сохраним ближайшие точки пересечения в приоритетной очереди.

Обработка событий обоих типов выполняется с такой же асимптотикой, что и в алгоритме для выпуклых полигонов. Основной вклад в асимптотику вносит вычисление [math] split\ event'[/math]ов, когда нам нужно пробежаться по всем рёбрам и найти противолежащее. Отсюда и получается итоговая асимптотика [math] \mathcal{O}(n^2) [/math].

Случай полигонов с дырами

Данный алгоритм может работать и с многоугольниками, содержащими дыры, если они ориентированы по часовой стрелке, чтобы внутренняя область многоугольника лежала слева от рёбер. И в самом начале алгоритма каждый замкнутый контур помещается в свой [math] \mathrm{LAV} [/math] в множестве [math] \mathrm{SLAV} [/math].

Пример не для слабонервных

Особенности реализации и другие частные случаи

TODO: Совпадение нескольких split event'ов в одной точке

TODO: Накладывание рёбер друг на друга

Алгоритм построения с помощью Motorcycle graph

Рассмотрим алгоритм построения на основе мотографов.

TODO: Алгоритм на мотографах

Другие алгоритмы

Существует простой в понимании и реализации алгоритм для построения на основе триангуляции, который работает за время [math] \mathcal{O}(n^3 \log n)[/math]^[3]. Aichholzer смог обобщить этот алгоритм для построения произвольного планарного графа^[4]. Также автором в его оригинальной статье был представлен алгоритм построения данной структуры, базирующийся на понятии волнового фронта (англ. wavefront). Этот алгоритм может быть реализован за время [math] \mathcal{O}(n^3)[/math] с использованием [math] \mathcal{O}(n)[/math] памяти либо с использованием приоритетной очереди за время [math] \mathcal{O}(n^2 \log n)[/math] и [math] \mathcal{O}(n^2)[/math] памяти^[5]. Известен алгоритм построения для монотонных полигонов за время [math] \mathcal{O}(n \log n)[/math] с использованием [math] \mathcal{O}(n)[/math] памяти^[6].

В данном конспект был (P.S. точнее, ещё будет) представлен алгоритм на основе мотографов, который придумали Stefan Huber и Martin Held. Они говорят, что даже смогли реализовать этот алгоритм, но код нигде не выкладывали.

См. также

Примечания

Источники информации

[1] Wikipedia — Fold-and-cut theorem

[2] Stepan Obdrazalek, "The Angular bisector network Implementation and the CGAL library"

[3] Stefan Huber, Martin Held, "Straight Skeletons and their Relation to Triangulations"

[4] Oswin Aichholzer, Franz Aurenhammera, "Straight Skeletons for General Polygonal Figures in the Plane"

[5] Oswin Aichholzer, Franz Aurenhammera, "A Novel Type of Skeleton for Polygons"

[6] Therese Biedl, Martin Held, Stefan Huber, Dominik Kaaser, Peter Palfrader, "Straight Skeletons of Monotone Polygons"

[1]

[2]

[3]

[4]

[5]

[6]