Теорема о гигантской компоненте. Поиск в ширину в случайном графе

Теорема о гигантской компоненте

Перед формулировкой основной теоремы данного раздела дадим определение некоторых понятий, которые будут использованы в дальнейшем, а также приведем необходимые далее утверждения.

Определение:

Простейший ветвящийся процесс. Пусть [math]Z_1,\dotsc Z_n,\dotsc [/math] — независимые пуассоновские величины с одним и тем же математическим ожиданием [math]\lambda[/math]. Положим [math]Y_0 = 1, Y_i = Y_{i - 1} + Z_i - 1[/math].

Представлять себе описанный только что процесс можно так: в начальный момент времени есть одна активная частица. Затем она создает [math]Z_1 \geq 0[/math] (может быть достигнуто, так как величина [math]Z_1[/math] равна нулю с положительной вероятностью) активных потомков и перестает быть активной. На следующем шаге все повторяется: какая-то частица (порядок роли не играет) порождает [math]Z_2[/math] новых частиц, а сама перестает быть активной, и так далее. Данный процесс может как завершиться (частицы перестанут быть активными), так и продолжаться бесконечно.
Говоря в терминах данного выше определения, [math]Y_i[/math] и [math]Z_i[/math] — количество активных и порожденных частиц в момент времени [math]t[/math], соответственно.

Теорема (1):

Пусть [math]\lambda \leq 1[/math]. Тогда с вероятностью 1 процесс [math]Y_t[/math] вырождается, т.е. [math]P(\exists t: Y_t = 0) = 1[/math].

Теорема (2):

Пусть [math]\lambda \ge 1[/math]. Пусть [math]\gamma \in (0, 1)[/math] — единственное решение уравнения [math]1 - \gamma = e^{-\lambda \gamma}[/math]. Тогда процесс [math]Y_t[/math] вырождается с вероятностью [math]1 - \gamma[/math], т.е. [math]P(\exists t: Y_t \leq 0) = 1 - \gamma[/math].

Определение:

Ветвящийся процесс на случайном графе. Пусть [math]Z_1,\dotsc Z_n,\dotsc [/math] — независимые пуассоновские величины с одним и тем же математическим ожиданием [math]\lambda[/math]. Положим [math]Y_0 = 1, Y_i = Y_{i - 1} + Z_i - 1[/math].

В произвольном графе [math]G = (V,E)[/math] зафиксируем [math]v_1 \in V[/math]. Пометим ее как активную, а все остальные вершины — нейтральными. Выберем среди нейтральных вершин всех соседей вершины [math]v_1[/math]. После этого пометим вершину [math]v_1[/math] как неактивную , а смежных с ней — как активных, а все остальные вершины — нейтральными.

Снова зафиксируем какую-нибудь активную вершину [math]v_2[/math], и повторим процесс, не меняя статус остальных уже активных вершин.

Продолжая этот ветвящийся процесс, мы в конце концов получим лишь неактивные (образующие компоненту, содержащую [math]v_1[/math]) и нейтральные вершины.
Данный процесс очень похож на поиск в ширину, этим свойством мы воспользуемся позднее.

Обозначим число активных вершин в момент времени [math]t[/math] через [math]Y_t[/math], число нейтральных вершин — через [math]N_t[/math], а число соседей вершины, которую собираемся пометить как неактивную, — через [math]Z_t[/math]. Тогда [math]Y_0 = 1,Y_t = Y_{t − 1} + Z_t − 1[/math]. Все введенные величины зависят от графа [math]G[/math] и от последовательности выбираемых вершин [math]v_1,\dotsc[/math].

Если [math]G[/math] посчитать случайным, то при любом выборе вершин [math]v_1,\dotsc[/math] получатся случайные величины [math]Y_t, N_t, Z_t[/math] на пространстве [math]G(n, p)[/math].

Теорема о гигантской компоненте

Теорема (о гигантской компоненте):

Рассмотрим модель [math]G(n, p)[/math]. Пусть [math]p = \dfrac{ c }{n}[/math]. Если [math]c \lt 1[/math], то найдется такая константа [math]\beta[/math], зависящая от [math]c[/math], что а.п.н. (асимптотически почти наверное) размер каждой связной компоненты случайного графа не превосходит [math]\beta \ln n[/math]. Если же [math]c \gt 1[/math], то найдется такая константа [math]\gamma[/math], зависящая от [math]c[/math], что а.п.н. в случайном графе есть ровно одна компонента размера [math]\geq\gamma n[/math]. Размер остальных компонент не превосходит [math]\beta \ln n[/math].

Доказательство:

[math]\triangleright[/math]

Приведем здесь идеи, изложенные А.М. Райгородским, основанные на доказательстве Р. Карпа. Такой формат позволит понять основные идеи и логику рассуждений. Строгий вариант приведен в . Здесь и далее: [math]Binomial[/math] — биномиальное распределение. Случай [math]c \lt 1[/math]. Положим [math]t_0=[\beta \ln n][/math], где [math]\beta[/math] — константа, которая будет подобрана далее. Нам хочется доказать, что с большой вероятностью каждая из компонент случайного графа имеет размер, меньший или равный [math]t_0[/math]. Но размер компоненты — это момент вырождения процесса [math]Y_t[/math] на случайном графе. Значит, интересующее нас утверждение можно записать в следующем виде: [math]P_{n, p}(\exists v_1 : Y_{t_0} \gt 0) \rightarrow 0, n \rightarrow \infty[/math] Поскольку [math]P_{n, p}(\exists v_1 : Y_{t_0} \gt 0) \le nP_{n, p}(Y_{t_0} \ge 0)[/math], достаточно найти такое [math]\beta[/math], при котором [math]P_{n, p}(Y_{t_0} \gt 0) = o\left(\frac{1}{n}\right).[/math] [math]P_{n, p}(Y_{t_0} \gt 0) = P_{n, p}(\xi_{t_o} \geq t_0) \thickapprox P_{n, p}(Binomial(n, 1 - (1 - p)^{t_0}) \geq t_0) \thickapprox[/math] (с учетом асимптотики [math]1 - (1 - p)^{t_0} \thicksim pt_0) [/math] [math]\thickapprox P_{n, p}(Binomial(n, pt_0) \geq t_0) \thickapprox[/math] (с учетом центральной предельной теоремы) [math] \thickapprox \int\limits_{\frac{t_0 - npt_0}{\sqrt{npt_0(1 - pt_0)}}}^\infty \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx[/math]. Поскольку [math]c \lt 1[/math], нижний предел интегрирования имеет порядок [math]\sqrt{t_0}[/math]. Таким образом, весь интеграл не превосходит величины [math]e^{−\delta t_0}[/math]. Выберем [math]\beta[/math] таким, чтобы [math]e^{−\delta t_0}[/math] оказалось меньше, чем [math]e^{-2 \ln n} = \dfrac{1}{n^2}[/math], и в случае [math]c \lt 1[/math] теорема доказана. Случай [math]c \gt 1[/math]. В данном случае ветвящийся процесс на графе нужно «запускать» не один раз, а многократно. Только так удается доказать, что а.п.н. хотя бы в одном запуске возникнет гигантская компонента. Подробности можно найти в , мы же лишь поясним, откуда в текущей ситуации появляется [math]\gamma[/math] из формулировки теоремы 2 и почему она совпадает с одноименной константой из той же теоремы. Чтобы доказать, что есть гигантская компонента, необходимо, чтобы ветвящийся процесс на графе не вырождался даже при [math]t \thickapprox \gamma n[/math], то есть: [math]P_{n, p}(Y_{t} \le 0)\rightarrow 0, t \thickapprox \gamma n, n \rightarrow \infty[/math] Так как по условию [math]p = \dfrac{ c }{n}[/math], то при [math]t \thicksim \alpha n[/math] выполнено: [math] 1 - (1 - p)^t \thicksim 1 - e^{-pt} \thicksim 1 - e^{-c\alpha}[/math] Применим центральную предельную теорему к [math]P_{n, p}(Y_{t} \le 0)\thickapprox P_{n, p}(Binomial(n, 1 - e^{-c\alpha}) \le \alpha n).[/math] Пределы интегрирования в данном случае: от [math]-\infty[/math] до [math]\dfrac{\alpha n - n(1 - e^{-c\alpha})}{\sqrt{n(1 - e^{-c\alpha})e^{-c\alpha}}}[/math]. Если [math]\alpha \lt 1 - e^{-c\alpha}[/math], то мы получим искомое стремление вероятности к нулю. Если [math]\alpha \gt 1 - e^{-c\alpha}[/math], то вероятность, напротив, будет стремиться к единице. Таким образом, критическое значение [math]\alpha[/math], вплоть до которого есть именно стремление к нулю, — это решение уравнения [math]\alpha = 1 - e^{-c\alpha}[/math] или, что равносильно, [math]1 - \alpha = e^{-c\alpha}[/math]. А это и есть уравнение из теоремы 2, если заменить [math]\lambda[/math] на [math]c[/math].

[math]\triangleleft[/math]

Обход случайного графа

Приведем ряд утверждений, которые будут использованы в дальнейшем. Их доказательство, а также более детальный рассказ можно найти здесь.

Лемма (1):

Пусть [math]d \gt 1[/math]. Тогда вероятность [math]p[/math], что [math]size(cc(v)) = O(\log n)[/math] ([math]cc[/math] — компонента связности, содержащая [math]v[/math]): [math]p \lt 1[/math] — константа.

Доказательство:

[math]\triangleright[/math]

Главная идея доказательства, которую мы будем использовать в дальнейшем — изменение алгоритма поиска в ширину таким образом, чтобы только что открытые вершины были выбраны из множества фиксированного размера. Такая модификация превращает поиск в ширину в ветвящийся процесс.

[math]\triangleleft[/math]

Теорема (4):

Пусть [math]p = \frac{d}{n}, d \gt 1[/math]. [math] \begin{equation*} \begin{cases} & \text{1) Найдутся такие $c_1, c_2$, что с $p \leq \frac{1}{n}$ $\exists cc: size(cc) \in (c_1\log n; c_2n)$;} \\ & \text{2) Число вершин в компонентах размера $O(\ln n)$ а.п.н. $\leq cn, c \lt 1$.} \\ & \quad\:\text{Тогда с $p = 1 - o(1)$ существует компонента связности размера $\Omega (n)$;} \\ \end{cases} \end{equation*} [/math]

Поиск в ширину

Рассмотрим граф [math]G(n, p)[/math]. Проанализируем его структуру по мере роста [math]p[/math]:

• [math]p = 0:[/math] граф состоит только из изолированных вершин. С ростом [math]p[/math] в нем появляются ребра, компоненты связности получающегося леса объединяются.
  
• [math]p = o\left(\frac{1}{n}\right):[/math] граф а.п.н. является лесом;
  
• [math]p = \frac{d}{n}:[/math] появляются циклы. При [math]d \lt 1[/math] размер каждой из компонент связности равен [math]\Omega(\log n)[/math]. Число компонент связности, содержащих только один цикл — константа, зависящая от [math]n[/math]. Таким образом, граф состоит из леса и компонент, содержащих единственный цикл без компонент размера [math]\Omega(\log n)[/math];
  
• [math]p = \frac{1}{n}:[/math] начинает образовываться гигантская компонента. Этот процесс происходит в два этапа:
  
  • [math]p = \frac{1}{n}: [/math] возникают компоненты из [math]n^{\frac{2}{3}}[/math] вершин, а.п.н. являющиеся деревьями;
    
  • [math]p = \frac{d}{n}, d \gt 1: [/math] появляется гигантская компонента размером, пропорциональным количеству вершин во всем графе;
    
• [math]p \geq \frac{d}{n}:[/math] все неизолированные вершины оказываются в гигантской компоненте;
  
• [math]p \geq \frac{\ln n}{2n}:[/math] в графе остаются только изолированные плюс гигантская компонента;
  
• [math]p = \frac{\ln n}{n}:[/math] граф становится связным;
  
• [math]p = \frac{1}{2}:[/math] [math]\forall \varepsilon \gt 0\;\exists C\subseteq G,\quad C[/math] — клика [math]: |C| = (2 - \varepsilon )\log n[/math];
  

Чтобы вычислить размер компоненты связности, пройдемся с помощью поиска в ширину по ней, стартуя из произвольной вершины и переходя к очередной неисследованной вершине, только если ребро между ними существует (данный факт необходимо установить независимо от других ребер, с вероятностью [math]p = \frac{d}{n}[/math]). Если ребро существует, пометим следующую вершину как "открытую". Алгоритм закончит свою работу (обойдет всю компоненту связности), когда множество неисследованных "открытых" вершин станет пустым.

Проблема поиска в ширину

Проблема поиска в ширину на случайном графе

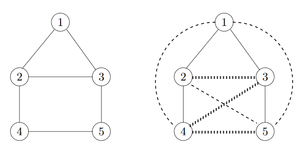
На данном изображении представлены результаты работы поиска в ширину , начавшемся в вершине [math]1[/math] на двух графах: в первом у всех ребер [math]p = 1[/math], во втором же факт существования ребра определялся по ходу работы алгоритма — ребра, отмеченные пунктиром, не существуют. Проблема возникает, когда алгоритм просто не доходит до каких-то ребер, не выясняя, существуют они или нет: находясь в вершине [math]2[/math], алгоритм не делал запрос о ребре [math](2, 3)[/math], так как у этому моменту вершина [math]3[/math] уже была исследована. Ребра, которые потенциально могли быть не изученными, помечены на рисунке точечным пунктиром.

Неоткрытые вершины

Будем считать шагом алгоритма поиска открытие новой вершины. После первых [math]i[/math] шагов алгоритма, любая из вершин, кроме стартовой, может быть неоткрытой с вероятностью [math]p = (1 - \frac{d}{n})^i[/math]. Пусть [math]z_i[/math] — число вершин, открытых за первые [math]i[/math] шагов алгоритма поиска. [math]z_i[/math] распределены как [math]Binomial(n − 1,1 − (1 - \frac{d}{n})^i)[/math].

Вероятность исчезновения

От поиска в ширину к ветвящимся процессам

Пользуясь идеями, изложенными в доказательстве леммы 1, перейдем от модифицированного поиска в ширину к ветвящемуся процессу. Этот процесс используется для генерации случайных деревьев, возможно, бесконечного размера.

Определение:

Вероятность исчезновения (extinction probability) — вероятность, того, что дерево ветвящегося процесса будет конечным (процесс завершится через конечное время).

Рассмотрим натуральное случайное число [math]y[/math], обозначающее количество потомков у очередной исследованной вершины. Каждый раз это значение выбирается случайно и независимо.
Процесс построения дерева заканчивается, образуя конечное дерево, когда у каждой вершины построены все ее потомки. Данный процесс может продолжаться бесконечно.
Пусть:

• [math]y \thicksim Binomial(s = n−c_1\log n, \frac{d}{n})[/math].
  
• [math]p′[/math] — вероятность того, что [math]size(cc(v)) = O(\log n)[/math] в модифицированном поиске в ширину.
  
• [math]q[/math] — вероятность окончания процесса.
  

Тогда [math]q \geq p′[/math], поскольку поиск в ширину, заканчивающийся с [math] \le c_1\log n[/math] вершинами, приводит к окончанию построения дерева.

[math]p_i = \binom{s}{i}(\frac{d}{n})^i(1 − \frac{d}{n})^{s − i}[/math] — вероятность, что [math]y[/math] производит [math]i[/math] потомков, а значит:
[math]\sum_{i = 0..s}p_i = 1[/math] и [math]\sum_{i = 0..s}ip_i = E(y) = \frac{ds}{n} \gt 1[/math].

Глубина дерева не меньше количества вершин, поэтому вероятность того, что процесс закончится с деревом глубины [math]t[/math], вычисляется по следующей формуле:
[math]a_t = p_0 + \sum_{i = 1..s}p_ia^i_{t - 1}[/math]

Вычисление вероятности исчезновения

Лемма (2):

Пусть [math]m \gt 1[/math]. Пусть [math]q[/math] — единственный корень [math]f(x) = x[/math] на [math][0, 1)[/math]. Тогда [math]f_j(x) = \lim_{j \to \infty}p(j) = q[/math] для [math]x\in [0,1)[/math].

Теорема (5):

Рассмотрим дерево, сгенерированное ветвящимся процессом. Пусть [math]f(x)[/math] — производящая функция числа потомков каждой вершины, а [math]k[/math] — ожидаемое количество потомков в каждой вершине. Тогда верно следующее: [math] \begin{equation*} \begin{cases} k \le 1 &\text{—$\;$ вероятность исчезновения равна 1, если вероятность} \\ & \;\;\;\;\;\,\text{появления ровно одного ребенка равна $1$;}\\ k \gt 1 &\text{—$\;$ вероятность исчезновения является }\\&\;\;\;\;\;\,\text{единственным решением $f(x) = x,\; x \in [0, 1)$;} \end{cases} \end{equation*} [/math].

В данной статье нами рассматривается простой случай ветвящегося процесса, в котором распределение количества потомков одинаково для каждой вершины.
Обозначим:

• [math]q[/math] — вероятность исчезновения;
  
• [math]y \thicksim Binomial(s = n−c_1\log n, \frac{d}{n})[/math] — количество потомков у очередной исследованной вершины;
  
• [math]p_i = \binom{s}{i}(\frac{d}{n})^i(1 − \frac{d}{n})^{s − i}[/math] — вероятность, что [math]y[/math] производит [math]i[/math] потомков.
  

Для того, чтобы вычислить вероятность исчезновения, воспользуемся производящей функцией:
[math]f(x) = \sum_{i = 0..\infty}p_ix^i,[/math] где [math]p_i[/math] — вероятность того, что [math]y = i[/math]

Так как [math]q[/math] — вероятность конечности алгоритма, то, если у корневой вершины [math]i[/math] потомков, построение каждого из поддеревьев должно завершиться, и это произойдет с вероятностью [math]q^i[/math]:
[math]q = \sum_{i = 0..\infty}p_iq^i[/math]
Благодаря чему, [math]q[/math] является корнем уравнения:
[math]x = \sum_{i = 0..\infty}p_ix^i \Leftrightarrow f(x) = x[/math]

Решение уравнения f(x)=x

Рассмотрим решение данного уравнения на [math][0; 1][/math].
[math]x = 1[/math] — всегда решение данного уравнения, так как [math]\sum_{i = 0..\infty}p_i1^i = \sum_{i = 0..\infty}p_i = 1 = x[/math].
Введем обозначения: [math]k[/math] — количество потомков вершины, а [math]m = f'(1)[/math], тогда [math]m = f'(1) = \sum_{i = 1..\infty}ip_i = E(k)[/math].
Кажется, что при [math]m \gt 1[/math] дерево будет расти вечно, так как каждая вершина в момент времени [math]j[/math] должна иметь потомков, однако при [math]p_0 \gt 0[/math] с положительной вероятностью у корня может вообще не быть потомков. В исходном [math]G(n,\frac{d}{n})[/math] [math]m[/math] играет роль [math]d[/math], ввиду того, что [math]d = E(k)[/math].
Пользуясь леммой 2 и теоремой 5, можно доказать, что:

1. [math]m \lt 1 \vee m = 1 \wedge p_1 \lt 1[/math] — вероятность исчезновения [math] = 1[/math];
   
2. [math]m = 1 \wedge p_1 = 1[/math] — вероятность исчезновения [math] = 0[/math];
   
3. [math]m \gt 1[/math] — вероятность исчезновения [math] \lt 1[/math], но, если [math]p_0 = 0[/math], процесс не завершится, так как у каждой вершины найдется по крайней мере один потомок;
   

Подробное описание доказательства данного факта, а также самих утверждений можно найти здесь.

Вывод

Используя результаты, полученные в предыдущей части, сделаем вывод о вероятности окончания работы поиска в ширину на случайном графе [math]G(n, \frac{d}{n})[/math]. Рассчитав [math]p_0[/math] и [math]p_1[/math], можно сделать следующие выводы:
[math] \begin{equation*} \begin{cases} d \lt 1\;\vee\; d = 1\;\wedge\; p_1 \lt 1&\text{—$\;$ процесс завершится с вероятностью один;}\\ d = 1\;\wedge\; p_1 = 1&\text{—$\;$ процесс будет протекать бесконечно;}\\ d \gt 1&\text{—$\;$ вероятность исчезновения меньше единицы, но, если $p_0 = 0$, процесс не завершится, так как у каждой вершины}\\&\;\;\;\;\;\,\text{найдется по крайней мере один потомок;}\\ \end{cases} \end{equation*} [/math]

См. также

• Случайная величина
• Случайные графы
• Обход в ширину
• Производящая функция