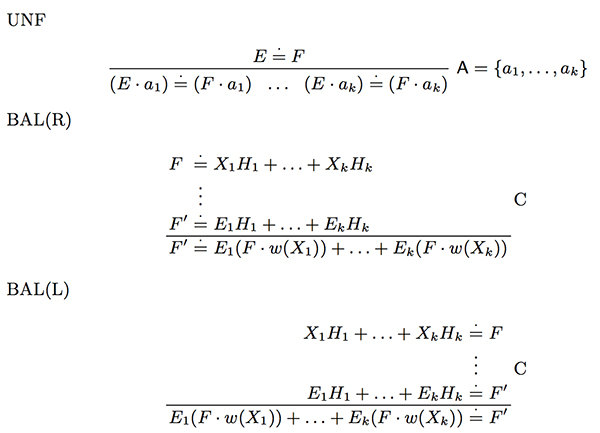Предположим детерминированный строгий автомат с единственным состоянием с элементами, представленный тройкой:
- входной алфавит на ленте [math]\Sigma[/math],
- стековым алфавит [math]\Gamma[/math],
- множеством переходов [math]\Delta[/math].
Мы предполагаем наличие полного порядка на [math]\Sigma[/math],и говорим, что слово [math]u[/math] короче слова [math]v[/math] если [math]|u| \lt |v|[/math] или [math]|u| = |v|[/math] и [math]u[/math] лексикографически меньше [math]v[/math]. Пусть [math]E, F, G,\dotsc[/math] — допустимые конфигурации.
| Определение: |
| Конфигурация [math]E[/math] после слова [math]u[/math], обозначается [math]E \cdot u[/math] — единственная допустимая конфигурация [math]F[/math] такая что [math](E, u) \rightarrow F[/math], которая может быть и [math]\emptyset[/math]. |
| Определение: |
| Язык, задаваемой конфигурацией [math]E[/math] — [math]L(E) = \{ E \mid (E \cdot u) = \varepsilon \}[/math]. |
| Определение: |
| Две конфигурации [math]E[/math] и [math]F[/math] эквивалентны — [math]L(E) = L(F)[/math], обозначается [math]E \sim F[/math]. |
Равенство задаваемых языков также может быть приблизительным.
| Определение: |
Конфигурафии [math]E[/math] и [math]F[/math] [math]n[/math]-эквивалентны, обозначается [math]E \sim_n F, n \geqslant 0[/math] — они принимают одни и те же слова, длина которых не больше [math]n[/math]:
для всех слов [math]w[/math], таких что [math]|w| \leqslant n, (E \cdot w) = \varepsilon[/math] тогда и только тогда, когда [math](F \cdot w) = \varepsilon[/math]. |
| Утверждение: |
Справедливы следующие факты:
- [math]E \sim F[/math] тогда и только тогда, когда для любого [math] n \geqslant 0[/math] выполняется [math]E \sim_n F[/math].
- Если [math]E \nsim F[/math], то существует [math] n \geqslant 0[/math] такой, что [math]E \sim_n F[/math] и [math]E \nsim_{n+1} F[/math].
- Если [math]E \sim F[/math], то для любого [math]u \in \Sigma^*[/math], [math](E \cdot u) \sim (F \cdot u)[/math].
- [math]E \sim_{n} F[/math], тогда и только тогда, когда для любого [math]u \in \Sigma^*[/math], где [math]|u| \leqslant n[/math], [math](E \cdot u) \sim_{n-|u|} (F \cdot u)[/math].
- Если [math]E \sim_{n} F[/math] и [math]0 \leqslant m \lt n[/math], то [math]E \sim_{m} F[/math].
- Если [math]E \sim_{n} F[/math] и [math]F \nsim_{n} G[/math], то [math]E \nsim_{n} G[/math].
|
| Определение: |
| Для каждого стекового символа [math]X[/math] словом [math]w(X)[/math] называется самое короткое слово в множестве [math]\{u \mid (X \cdot u) = \varepsilon \}[/math]. |
| Определение: |
| [math]E = E_1G_1 + \ldots + E_nG_n[/math] находится в форме голова/хвост, если голова [math]E_1 + \ldots +E_n[/math] допустима и хотя бы один [math]E_i= \emptyset[/math], и каждый хвост [math]G_i = \emptyset[/math]. |
Приведём некоторые свойства формы голова/хвост. Эквивалентность и [math]n[/math]-эквивалентность языков согласуются с операцией суммы. Следовательно, форма голова/хвост позволяет подставить эквивалентное выражение в хвост (т.к. допустимость сохраняется).
| Утверждение: |
Пусть [math]E = E_1G_1 + \ldots + E_nG_n[/math], тогда справедливы следующие факты:
- Если [math](E_i \cdot u) = \varepsilon[/math], то для всех [math]j \neq i[/math] выполняется [math](E_j \cdot u) = \emptyset[/math] и [math](E \cdot u) = G_i[/math].
- Если [math](E_i \cdot u) = \emptyset[/math], то [math](E \cdot u) = (E_1 \cdot u)G_1 + \ldots + (E_n \cdot u)G_n[/math].
- Если [math]H_i \neq \emptyset, 1 \leqslant i \leqslant n[/math], то [math]E_1H_1 + \ldots + E_nH_n[/math] в форме голова/хвост.
- Если каждая [math]H_i \neq \emptyset[/math] и каждая [math]E_i \neq \varepsilon[/math] и для каждого [math]j[/math] такого, что [math]E_j \neq \emptyset[/math] выполняется [math]H_j \sim_m G_j[/math], то [math]E \sim{m+1} E_1H_1 + \ldots + E_nH_n[/math].
- Если [math]H_i \sim G_i, 1 \leqslant i \leqslant n[/math], то [math]E \sim E_1H_1 + \ldots + E_nH_n[/math].
|
Две конфигурации могут иметь одинаковые головы и разные хвосты, или одинаковые хвосты и различие в головах. Если [math]E[/math] представлена в форме голова/хвост[math]E_1G_1 + \ldots + E_nG_n[/math] и [math]F[/math] имеет схожую форму голова/хвост [math]F_1G_1 + \ldots + E_nF_n[/math], имеющая тот же самый хвост. Несоответствие между [math]E[/math] и [math]F[/math], соответственное этому представлению — это [math] \max_{1 \leqslant i \leqslant n} \{|E_i|, |F_i| \}[/math]. Если несоответствие равно 0, то конфигурации одинаковы.
Замечание: любая пара конфигураций [math]E[/math] и [math]F[/math] имеет форму голова/хвост включающую в себя одинаковые хвосты: [math] E = EG[/math] и [math]F = FG[/math], где [math]G = \varepsilon[/math].
| Определение: |
| Если [math]E = E_1G_1 + \ldots + E_nG_n[/math] и [math]F = F_1F_1 + \ldots + F_nF_n[/math], тогда [math]F[/math] в его форме голова/хвост — хвостовое дополнение [math]E[/math] в его форме голова/хвост обеспечивается [math]H_i = K^i_1G_1 + \ldots + K^i_nG_n, 1 \leqslant i \leqslant m[/math]. Когда [math]F[/math] — хвостовое дополнение [math]E[/math], относящиеся к нему дополнение [math]e[/math] — кортеж из m элементов [math](K^1_1+ \ldots +K_n^1, \ldots ,K_1^m + \ldots +K_n^m)[/math] без [math]G_is[/math], и говорится, что [math]F[/math] дополняет [math]E[/math] с помощью [math]e[/math]. |
Можно рассматривать дополнения как матрицы. Если [math]E''[/math] расширяет [math]E'[/math] с помощью [math]e[/math] и [math]E'[/math] расширяет [math]E[/math] с помощью [math]f[/math], то [math]E''[/math] расширяет [math]E[/math] с помощью [math]ef[/math](в смысле умножения матриц).
Особый случай расширения возникает когда хвосты одинаковы. Если [math]E = E_1G_1 + \ldots + E_nG_n[/math] и [math]F = F_1G_1+ \ldots +F_nG_n[/math], тогда [math]F[/math] расширяет [math]E[/math] с помощью [math]e = ( \varepsilon + \emptyset + \ldots + \emptyset , \ldots , \emptyset + \emptyset + \ldots + \varepsilon)[/math]. Расширение [math]e[/math] сокращается до тождества [math]\varepsilon[/math] (аналог единичной матрицы).
Процедура проверки
Процедура для проверки [math]E \sim F[/math] — направленное дерево доказательства из выражений, имеющие графическое представление, со стартовой целью [math]E \doteq F[/math]. Чтобы проверить конфигурации на эквивалентность мы будем разбивать выражения на подвыражения используя правила вывода. Существует всего три правила вывода:
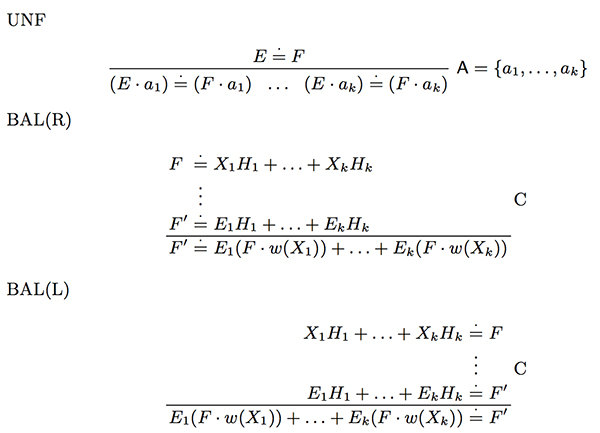
где [math]C[/math] — это условие:
- Каждая [math]E_i \neq \varepsilon[/math] и хотя бы одна [math]H_i \neq \varepsilon[/math].
- Имеется ровно [math] \max_{1 \leqslant i \leqslant k } \{ |w(X_i)| : E_i \neq \emptyset \}[/math] применений [math]UNF[/math] между верхним и нижним выражением, и не применяются другие правила.
- Если [math]u[/math] — это слово относящиеся к полседовательности операция [math]UNF[/math], то [math]E_i = (X_i \cdot u)[/math] для каждого [math]i : 1 \leqslant i \leqslant k \[/math].
[math]UNF[/math] — означает развертывание(англ. unfold), редуцирует выражение [math]E \doteq F[/math] на подвыражения [math](E \cdot a) \doteq (F \cdot a)[/math] для каждого [math]a[/math] из алфавита. Если исходное выражение истинно, то истинны и его подвыражения. Более строгая версия этого факта зафиксирована в следующих фактах:
- Если [math]E \sim F[/math] и [math]a \in \sigma[/math], то [math](E \cdot a) \sim (F \cdot a)[/math].
- Если [math]E \nsim_{m+1} F[/math], то для какого-то [math]a \in \sigma[/math] выполняется [math](E \cdot a) \nsim_m (F \cdot a)[/math].
Применение [math]BAL[/math] использует [math]F[/math], если [math]F[/math] — конфигурация в исходном выражении правила вывода. Если есть успешное представление, корень которого является ложным, то существует ветвь таблицы, внутри которой каждое подвыражение является ложной. Если два исходных выражения принадлежат последующей ветке, то подвыражение сохраняет уровень ложности второй предпосылки. Запишем это более строго:
| Утверждение: |
Справедливы следующие факты о [math]BAL[/math]:
- Если [math]X_1H_1+ \ldots +X_kH_k \sim F[/math] и [math]E_1H_1+ \ldots +E_kH_k \sim F'[/math], тогда [math]E_1(F \cdot w(X_1))+ \ldots +X_k(F \cdot w(X_k)) \sim F'[/math].
- Если [math]X_1H_1+ \ldots +X_kH_k \sim_{n+m} F[/math] и [math]E_1H_1+ \ldots +E_kH_k \nsim_{n+1} F'[/math] и каждая [math]E_i \neq \varepsilon[/math] и [math]m \geqslant \max \{ |w(X_i)| \mid E_i \neq \emptyset \}[/math], то [math]E_1(F \cdot w(X_1))+ \ldots +E_k(F \cdot w(X_k)) \nsim_{n+1} F'[/math].
|
| Теорема (о расширении): |
Пусть есть два семейства выражений [math]g(i), h(i), 1 \leqslant i \leqslant 2^n[/math], и каждое выражение [math]g(i)[/math] имеет форму [math]E_1G^i_1+ \ldots +E_nG^i_n=F_1G^i_1+ \ldots +F_nG^i_n[/math] и каждое выражение [math]h(i)[/math] имеет форму [math]E_1H^i_1+ \ldots +E_nH^i_n=F_1H^i_1+ \ldots +F_nH^i_n[/math].
Пусть расширения [math]e_1, \ldots ,e_n[/math] такие, что для каждого [math]e_j[/math] и [math]i \geqslant 0, g(2^j i + 2^{j-1} + 1)[/math] расширяет [math]g(2^j i + 2^{j-1})[/math] с помощью [math]e_j[/math] и [math]h(2^j i + 2^{j-1} + 1)[/math] расширяет [math]h(2^j i + 2^{j-1})[/math] с помощью [math]e_j[/math].
Если для каждое выражение [math]g(i)[/math] верно на уровне [math]m, i: 1 \leqslant i \leqslant 2^n[/math], и для каждого выражения [math]h(j),j: 1 \leqslant j \lt 2^n[/math] верно на уровне [math]m[/math],
то [math]h(2^n)[/math] верно на уровне [math]m[/math]. |
| Определение: |
| Пусть ветка доказательства состоит из выражений [math]d(0), \ldots ,d(l)[/math]. Выражение [math]d(l)[/math] удовлетворяет теореме о расширении если существеют выражения [math]g(i),h(i),1 \leqslant i \leqslant 2^n[/math], и расширения [math]e_1, \ldots ,e_n[/math] как описано в теормере о расширении, и выражения принадлежат [math]\{d(0), \ldots ,d(l)\}[/math], и [math]h(2^n)[/math] — это [math]d(l)[/math] и есть хотя бы одно применение [math]UNF[/math] между выражением [math]h(2^n-1)[/math] и [math]d(l)[/math]. |
| Определение: |
Пусть ветка доказательства состоит из выражений [math]g(0), \ldots ,g(n)[/math], где [math]g(0)[/math] — корневое выражение. Выражение [math]g(n)[/math] — это финальное выражние находящиеся одном из следующих условий:
- Если [math]g(n)[/math] — это тождество [math]E \doteq E[/math], то [math]g(n)[/math] — это успешное финальное выражение.
- Если [math]g(n)[/math] удовлетворяет теореме о расширении, то [math]g(n)[/math] — это успешное финальное выражение.
- Если [math]g(n)[/math] имеет форму [math]E \doteq \emptyset[/math] или [math]\emptyset \doteq E[/math] (и [math]E \neq \emptyset[/math]), тогда [math]g(n)[/math] — это неуспешное финальное выражение.
|
| Лемма: |
В бесконечной ветке доказательств состоящей из выражений [math]g(0), \ldots ,g(n), \ldots [/math] где [math]g(0)[/math] — корневое выражение, существует такое [math]n[/math], что [math]g(n)[/math] — финальное выражение. |
Введём несложную процедуру проверки [math]E \sim F[/math], и зададим её пошагово.
- Шаг [math]0[/math]: начинаем с корневого выражение [math]g(0)[/math], [math]E \doteq F[/math], что является вершиной ветвления ветки [math]g(0)[/math].
- Шаг [math]n+1[/math]: Если текущая вершина ветвления [math]g(n)[/math] ветки [math]g(0), \ldots ,g(n)[/math] — это неуспешное финальное выражение, то прерываемся и возвращаем "некорректное представление";
Если каждая вершина ветвления [math]g(n)[/math] ветки [math]g(0), \ldots ,g(n)[/math] — успешное финальное выражение, тогда возвращаем "корректное представление";
Иначе для каждой вершины ветвления [math]g(n)[/math] ветки [math]g(0), \ldots ,g(n)[/math], которая не является финальной целью, применяем следующие правило, и подвыражения, получившиеся в результате, — новые вершины ветвления расширенных веток.
| Теорема: |
Справедливы следующие факты:
- Если [math]E \nsim F[/math], то процедура проверки вернёт "некорректное представление".
- Если [math]E \sim F[/math], то процедура проверки вернёт "корректное представление".
|
См. также
Источники информации