|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | {{ | | {{ |
| | Теорема|statement= | | Теорема|statement= |
| Теорема: |
Любая булева функция от [math]n[/math] аргументов [math]f(x_1, x_2, \ldots, x_n)[/math] в базисе [math]B = \{\neg, \lor, \land\}[/math] имеет схемную сложность [math]size_B (f) = O\left(\dfrac{2^n}{n}\right)[/math]. |
Представление функции
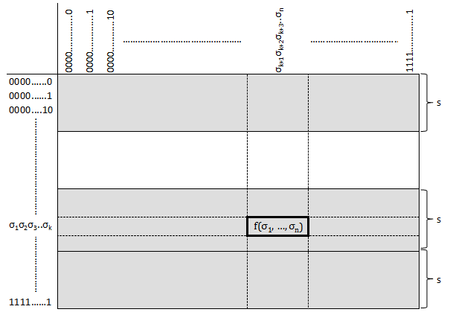
Рис.
[math]1[/math]. Описываемая таблица истинности, разделённая на полосы
Поделим аргументы функции на два блока: первые [math]k[/math] и оставшиеся [math](n - k)[/math].
Для удобства дальнейших рассуждений представим булеву функцию в виде таблицы, изображённой на рис. [math]1[/math]. Строки индексируются значениями первых [math]k[/math] переменных, столбцы — значениями оставшихся [math](n - k)[/math]; таким образом, на пересечении столбца и строки находится значение функции для соответствующего набора аргументов.
Разделение на полосы
Разделим таблицу на горизонтальные полосы шириной [math]s[/math] (последняя полоса, возможно, будет короче остальных; её ширину обозначим [math]s'[/math]). Пронумеруем полосы сверху вниз от [math]1[/math] до [math]p=\left\lceil\dfrac{2^k}{s}\right\rceil[/math].
Рассмотрим независимо некоторую полосу. Заметим, что среди её столбцов при небольшом [math]s[/math] будет много повторений; далее про одинаковые столбцы, находящиеся в одной полосе, будем говорить, что они одного сорта.
| Определение: |
| Сорт некоторого столбца данной полосы — его класс эквивалентности по отношению поэлементного равенства столбцов данной полосы. |
Число сортов столбцов [math]i[/math]-й полосы обозначим как [math]t(i)[/math]. Понятно, что для любой полосы [math]t(i) \leqslant 2^s[/math] (для последней [math]t(p) \leqslant 2^{s'}[/math]).
Функция для одной полосы
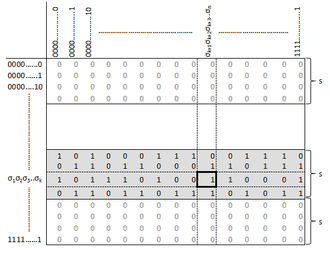
Рис.
[math]2[/math]. Значения, возвращаемые функцией
[math]g_{ij}[/math]Пусть для некоторого [math]i[/math]
- [math]\beta_{j}[/math] — произвольный столбец [math]i[/math]-й полосы [math]j[/math]-го сорта (точное положение столбца далее не будет иметь значения, по определению сорта)
- [math](\sigma_1^l, \sigma_2^l, \ldots, \sigma_k^l)[/math] — аргументы функции, соответствующие [math]l[/math]-й строке [math]i[/math]-й полосы.
Тогда введём булеву функцию
[math]g_{ij}(x_1, x_2, \ldots, x_k) = \begin{cases}
\beta_{jl}, \mbox{ if } \exists l \in [1; s]~(x_1, x_2, \ldots, x_k) = (\sigma_1^l, \sigma_2^l, \ldots, \sigma_k^l) \\
0, \mbox{ otherwise}
\end{cases}[/math]
Другими словами, если строка, соответствующая аргументам функции [math]x_1, x_2, \ldots, x_k[/math], находится в [math]i[/math]-й полосе, то функция возвращает значение, записанное в столбце сорта [math]j[/math] для этой строки. Если же эта строка находится в другой полосе, то функция вернёт [math]0[/math]. Иллюстрация принципа работы функции [math]g_{ij}[/math] приведена на рис. [math]2[/math].
Вывод исходной функции для фиксированной части параметров
Поскольку изначальный столбец [math](\sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_{n})[/math] складывается из столбцов соответствующих сортов в полосах,
[math]f(x_1, x_2, \ldots, x_k, \sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_{n}) = \bigvee\limits_{i = 1}^p g_{ij_i}(x_1, x_2, \ldots, x_k)[/math],
где [math]j_i[/math] — номер сорта столбца полосы [math]i[/math], являющегося соответствующей частью столбца [math](\sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_{n})[/math].
Мультиплексор и демультиплексор
Для упрощения доказательства теоремы будем использовать элементы мультиплексор и демультиплексор.
| Определение: |
Мультиплексор (англ. multiplexer) — логический элемент, получающий на вход
- [math]2^n[/math] булевых значений;
- [math]n[/math]-значное число [math]x[/math] в двоичном представлении
и возвращающий значение на [math]x[/math]-м входе. |
| Определение: |
Демультиплексор (англ. demultiplexer) — логический элемент, получающий на вход
- булево значение [math]z[/math];
- [math]n[/math]-значное число [math]x[/math] в двоичном представлении
и выводящий [math]z[/math] на [math]x[/math]-й из своих [math]2^n[/math] выходов. На все остальные выходы элемент выдаёт [math]0[/math]. |
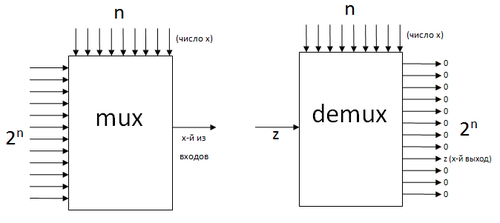 Мультиплексор слева, демультиплексор справа |
Оба элемента представимы схемами с числом элементов [math]O(2^n)[/math] с помощью базиса [math]B[/math].
Доказательство
В качестве доказательства ниже будет предложен вариант такой схемы для произвольной функции [math]f(x_1, x_2, \ldots, x_n)[/math] (представление Лупанова, англ. Lupanov [math](k, s)[/math]-representation).
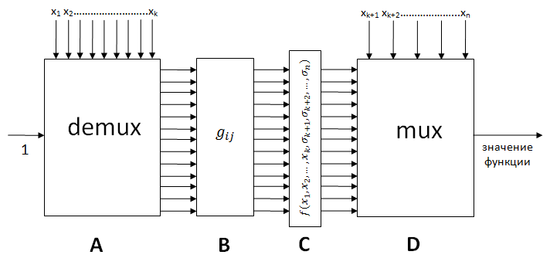
Для удобства поделим схему на блоки:
- Блок A — демультиплексор, которому на вход подали [math]1[/math] и [math](x_1, x_2, \ldots, x_k)[/math] в качестве двоичного представления числа.
- Блок B — схемная реализация всех [math]g_{ij}[/math]. Функцию [math]g_{ij}[/math] можно реализовать как [math]\bigvee\limits_{\beta_l = 1} y_{il}[/math], где [math]y_{il}[/math] — выдал ли демультиплексор [math]1[/math] на [math]l[/math]-м выходе [math]i[/math]-й полосы.
- Блок C — схемная реализация всех [math]f(x_1, x_2, \ldots, x_k, \sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_n)[/math]. (здесь [math]\sigma_i[/math] - фиксированные параметры, см. п. [math]3.1[/math])
- Блок D — мультиплексор, получающий на вход все [math]f(x_1, x_2, \ldots, x_k, \sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_n)[/math] и параметры функции [math]x_{k + 1}, x_{k + 2}, \ldots, x_n[/math] в качестве двоичного представления числа. Результат работы схемы — вывод мультиплексора.
Положим [math]s = \lfloor n - 2\log_2 n\rfloor[/math]; [math]k = \lfloor\log_2 n\rfloor[/math]. Тогда число элементов в блоках
- [math]L_A = O(2^k) = O(2^{\log_2 n}) = O(n)[/math]
- [math]L_B \leqslant (s - 1) \cdot (t(1) + t(2) + \ldots + t(p)) \lt sp \cdot 2^s = n \cdot \dfrac{2^n}{n^2} = \dfrac{2^n}{n}[/math]
- [math]L_C = O(p \cdot 2^{n - k}) = O\left(\dfrac{p}{n} \cdot 2^n\right) = O\left(\dfrac{2^n}{s}\right) = O\left(\dfrac{2^n}{n - 2\log_2 n}\right)[/math]
- [math]L_D = O(2^{n - k}) = O\left(\dfrac{2^n}{n}\right)[/math]
Итого, имеем схему c числом элементов [math]L_A + L_B + L_C + L_D = O(n) + O\left(\frac{2^n}{n}\right) + O\left(\dfrac{2^n}{n - 2\log_2 n}\right) + O\left(\dfrac{2^n}{n}\right) = O\left(\dfrac{2^n}{n}\right)[/math], откуда следует, что [math]size_B (f) = O\left(\dfrac{2^n}{n}\right)[/math], что и требовалось доказать.
См. также
Источник информации



