Теорема Поша — различия между версиями
(Новая страница: «{{Теорема |id = Th1 |about = Поша |statement = Пусть граф <tex> G </tex> имеет <tex>n \geqslant 3</tex> вершин. *Если дл...») |
м (rollbackEdits.php mass rollback) |
||
| (не показано 19 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| + | ==Теорема== | ||
| + | |||
{{Теорема | {{Теорема | ||
|id = Th1 | |id = Th1 | ||
| Строка 4: | Строка 6: | ||
Поша | Поша | ||
| − | |statement = Пусть граф <tex> G </tex> имеет <tex>n \geqslant 3</tex> вершин | + | |statement = Пусть граф <tex> G </tex> имеет <tex>n \geqslant 3</tex> вершин и выполнены следующие два условия: |
| − | * | + | *<tex> \forall </tex> <tex>k,\, 1 \leqslant k < (n-1)/2</tex>, число вершин со степенями, не превосходящими <tex>k</tex>, меньше чем <tex>k</tex> |
| − | * | + | *для нечетного <tex>n</tex> число вершин степени <tex>(n-1)/2</tex> не превосходит <tex>(n-1)/2</tex> |
| − | + | тогда <tex> G </tex> {{---}} [[Гамильтоновы графы|гамильтонов]] граф. | |
|proof = | |proof = | ||
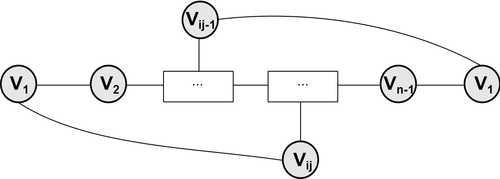
| + | [[Файл: Graph-Posha.png|500px|thumb|right|Гамильтонов цикл <tex> v_{1} v_{2} \dotsc v_{{i}_{j-1}} v_{n} v_{n-1} \dotsc v_{{i}_{j}} v_{1} </tex>]] | ||
Предположим, что теорема неверна. Пусть <tex> G </tex> {{---}} максимальный негамильтонов граф с <tex> n </tex> вершинами, удовлетворяющий условиям теоремы. | Предположим, что теорема неверна. Пусть <tex> G </tex> {{---}} максимальный негамильтонов граф с <tex> n </tex> вершинами, удовлетворяющий условиям теоремы. | ||
| − | Легко видеть, что добавление любого ребра в граф, обладающий указанными свойствами, приводит к графу, который также обладает этими свойствами. Таким образом, поскольку добавление к <tex> G </tex> произвольного ребра приводит к гамильтонову | + | Легко видеть, что добавление любого ребра в граф, обладающий указанными свойствами, приводит к графу, который также обладает этими свойствами. Таким образом, поскольку добавление к <tex> G </tex> произвольного ребра приводит к гамильтонову графу, любые две несмежные вершины соединимы простым гамильтоновым путем. |
| − | Покажем сначала, что всякая вершина, степень которой не меньше <tex> (n-1)/2 </tex>, смежна с каждой вершиной со степенью, большей чем <tex> (n-1)/2 </tex>. Не умаляя общности, допустим, что <tex> \deg v_{1} \geqslant (n-1)/2 </tex> и <tex> \deg v_{n} \geqslant n/2 </tex>, но вершины <tex> v_{1} </tex> и <tex> v_{n} </tex> не смежны. Тогда существует | + | Покажем сначала, что всякая вершина, степень которой не меньше <tex> (n-1)/2 </tex>, смежна с каждой вершиной со степенью, большей чем <tex> (n-1)/2 </tex>. Не умаляя общности, допустим, что <tex> \deg v_{1} \geqslant (n-1)/2 </tex> и <tex> \deg v_{n} \geqslant n/2 </tex>, но вершины <tex> v_{1} </tex> и <tex> v_{n} </tex> не смежны. Тогда существует простой гамильтонов путь <tex> v_{1} v_{2} \dotsc v_{n} </tex>, соединяющий <tex> v_{1} </tex> и <tex> v_{n} </tex>. Обозначим вершины, смежные с <tex> v_{1} </tex>, через <tex> v_{{i}_{1}}, \dotsc,v_{{i}_{k}} </tex>, где <tex> k = \deg v_{1} </tex> и <tex> 2=i_{1} < i_{2} < \dotsc < i_{k} </tex>. Ясно, что вершина <tex> v_{n} </tex> не может быть смежной ни с одной вершиной из <tex> G </tex> вида <tex> v_{{i}_{j-1}} </tex>, поскольку тогда в <tex> G </tex> был бы гамильтонов цикл <tex> v_{1} v_{2} \dotsc v_{{i}_{j-1}} v_{n} v_{n-1} \dotsc v_{{i}_{j}} v_{1} </tex>. |
Далее, так как <tex> k \geqslant (n-1)/2 </tex>, то <tex> n/2 \leqslant \deg v_{n} \leqslant n-1-k < n/2 </tex>, что невозможно. Поэтому <tex> v_{1} </tex> и <tex> v_{n} </tex> должны быть смежны. | Далее, так как <tex> k \geqslant (n-1)/2 </tex>, то <tex> n/2 \leqslant \deg v_{n} \leqslant n-1-k < n/2 </tex>, что невозможно. Поэтому <tex> v_{1} </tex> и <tex> v_{n} </tex> должны быть смежны. | ||
| Строка 22: | Строка 25: | ||
Отсюда следует, что если <tex> \deg v \geqslant n/2 </tex> для всех вершин <tex> v </tex>, то <tex> G </tex> {{---}} гамильтонов граф. В силу изложенного выше каждая пара вершин графа <tex> G </tex> смежна, т.е. <tex> G </tex> {{---}} полный граф. Мы пришли к противоречию, поскольку <tex> K_{n} </tex> {{---}} гамильтонов граф для всех <tex> n \geqslant 3 </tex>. | Отсюда следует, что если <tex> \deg v \geqslant n/2 </tex> для всех вершин <tex> v </tex>, то <tex> G </tex> {{---}} гамильтонов граф. В силу изложенного выше каждая пара вершин графа <tex> G </tex> смежна, т.е. <tex> G </tex> {{---}} полный граф. Мы пришли к противоречию, поскольку <tex> K_{n} </tex> {{---}} гамильтонов граф для всех <tex> n \geqslant 3 </tex>. | ||
| − | Таким образом, в <tex> G </tex> есть вершина <tex> v </tex> с <tex> \deg v < n/2 </tex>. Обозначим через <tex> m </tex> наибольшую среди степеней всех таких вершин. Выберем такую вершину <tex> v_{1} </tex>, что <tex> \deg v_{1} = m </tex>. По принятому предположению число вершин со степенями, не превосходящими <tex> m </tex>, не больше чем <tex> m < n/2 </tex>, поэтому должно быть более чем <tex> m </tex> вершин со степенями, превосходящими <tex> m </tex>, и, следовательно, не меньшими чем <tex> n/2 </tex>. В результате найдется некоторая вершина, скажем <tex> v_{n} </tex>, степени по крайней мере <tex> n/2 </tex>, не смежная с <tex> v_{1} </tex>. Так как <tex> v_{1} </tex> и <tex> v_{n} </tex> не смежны, то существует | + | Таким образом, в <tex> G </tex> есть вершина <tex> v </tex> с <tex> \deg v < n/2 </tex>. Обозначим через <tex> m </tex> наибольшую среди степеней всех таких вершин. Выберем такую вершину <tex> v_{1} </tex>, что <tex> \deg v_{1} = m </tex>. По принятому предположению число вершин со степенями, не превосходящими <tex> m </tex>, не больше чем <tex> m < n/2 </tex>, поэтому должно быть более чем <tex> m </tex> вершин со степенями, превосходящими <tex> m </tex>, и, следовательно, не меньшими чем <tex> n/2 </tex>. В результате найдется некоторая вершина, скажем <tex> v_{n} </tex>, степени по крайней мере <tex> n/2 </tex>, не смежная с <tex> v_{1} </tex>. Так как <tex> v_{1} </tex> и <tex> v_{n} </tex> не смежны, то существует простой гамильтонов путь <tex> v_{1} \dotsc v_{n} </tex>. Как и выше, обозначим через <tex> v_{{i}_{1}}, \dotsc, v_{{i}_{m}} </tex> вершины графа <tex> G </tex>, смежные с <tex> v_{1} </tex>, и заметим, что вершина <tex> v_{n} </tex> не может быть смежной ни с одной из <tex> m </tex> вершин <tex> v_{{i}_{j-1}} </tex> для <tex> 1 \leqslant j \leqslant m </tex>. Но поскольку <tex> v_{1} </tex> и <tex> v_{n} </tex> не смежны, а <tex> v_{n} </tex> имеет степень не меньше <tex> n/2 </tex>, то, как было показано в первой части доказательства, <tex> m </tex> должно быть меньше чем <tex> (n-1)/2 </tex>. Так как по предположению число вершин со степенями, не превосходящими <tex> m </tex>, меньше чем <tex> m </tex>, то хотя бы одна из <tex> m </tex> вершин <tex> v_{{i}_{j-1}} </tex>, скажем <tex> v' </tex>, должна иметь степень не меньше <tex> n/2 </tex>. Итак, мы установили, что степени двух несмежных вершин <tex> v_{n} </tex> и <tex> v' </tex> не меньше <tex> n/2 </tex>. Полученное противоречие завершает доказательство теоремы. |
}} | }} | ||
| − | + | ==Замечания== | |
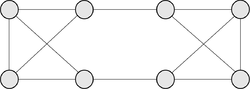
| + | [[Файл: Graph-Posha-Cubic.png|250px|thumb|right|Кубический гамильтонов граф]] | ||
| + | *Приведенное достаточное условие не является необходимым. Изображенный на рисунке кубический граф {{---}} гамильтонов, хотя ясно, что он не удовлетворяет условиям теоремы. | ||
| + | *Условия теоремы нельзя улучшить, так как при их ослаблении новое условие уже не будет достаточным для гамильтоновости графа. | ||
| + | |||
| + | |||
| − | |||
| − | |||
| − | Ограничивая условия теоремы Поша, получаем более простые, но менее сильные достаточные условия, найденные Оре и Дираком соответственно: | + | |
| + | |||
| + | |||
| + | |||
| + | ==Следствия== | ||
| + | |||
| + | Ограничивая условия теоремы Поша, получаем более простые, но менее сильные достаточные условия, найденные [[Теорема Оре|Оре]] и [[Теорема Дирака|Дираком]] соответственно: | ||
{{Теорема | {{Теорема | ||
| Строка 46: | Строка 58: | ||
}} | }} | ||
| − | ==Источники== | + | ==См. также== |
| + | *[[Теорема Оре]] | ||
| + | *[[Теорема Дирака]] | ||
| + | *[[Теорема Хватала]] | ||
| + | *[[Теорема Гринберга]] | ||
| + | *[[Теорема Редеи-Камиона]] | ||
| + | |||
| + | ==Источники информации== | ||
*Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 60 с. | *Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 60 с. | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Обходы графов]] | [[Категория: Обходы графов]] | ||
| + | [[Категория: Гамильтоновы графы]] | ||
Текущая версия на 19:42, 4 сентября 2022
Теорема
| Теорема (Поша): |
Пусть граф имеет вершин и выполнены следующие два условия:
|
| Доказательство: |
|
Предположим, что теорема неверна. Пусть — максимальный негамильтонов граф с вершинами, удовлетворяющий условиям теоремы. Легко видеть, что добавление любого ребра в граф, обладающий указанными свойствами, приводит к графу, который также обладает этими свойствами. Таким образом, поскольку добавление к произвольного ребра приводит к гамильтонову графу, любые две несмежные вершины соединимы простым гамильтоновым путем. Покажем сначала, что всякая вершина, степень которой не меньше , смежна с каждой вершиной со степенью, большей чем . Не умаляя общности, допустим, что и , но вершины и не смежны. Тогда существует простой гамильтонов путь , соединяющий и . Обозначим вершины, смежные с , через , где и . Ясно, что вершина не может быть смежной ни с одной вершиной из вида , поскольку тогда в был бы гамильтонов цикл . Далее, так как , то , что невозможно. Поэтому и должны быть смежны. Отсюда следует, что если для всех вершин , то — гамильтонов граф. В силу изложенного выше каждая пара вершин графа смежна, т.е. — полный граф. Мы пришли к противоречию, поскольку — гамильтонов граф для всех . Таким образом, в есть вершина с . Обозначим через наибольшую среди степеней всех таких вершин. Выберем такую вершину , что . По принятому предположению число вершин со степенями, не превосходящими , не больше чем , поэтому должно быть более чем вершин со степенями, превосходящими , и, следовательно, не меньшими чем . В результате найдется некоторая вершина, скажем , степени по крайней мере , не смежная с . Так как и не смежны, то существует простой гамильтонов путь . Как и выше, обозначим через вершины графа , смежные с , и заметим, что вершина не может быть смежной ни с одной из вершин для . Но поскольку и не смежны, а имеет степень не меньше , то, как было показано в первой части доказательства, должно быть меньше чем . Так как по предположению число вершин со степенями, не превосходящими , меньше чем , то хотя бы одна из вершин , скажем , должна иметь степень не меньше . Итак, мы установили, что степени двух несмежных вершин и не меньше . Полученное противоречие завершает доказательство теоремы. |
Замечания
- Приведенное достаточное условие не является необходимым. Изображенный на рисунке кубический граф — гамильтонов, хотя ясно, что он не удовлетворяет условиям теоремы.
- Условия теоремы нельзя улучшить, так как при их ослаблении новое условие уже не будет достаточным для гамильтоновости графа.
Следствия
Ограничивая условия теоремы Поша, получаем более простые, но менее сильные достаточные условия, найденные Оре и Дираком соответственно:
| Теорема (Следствие 1): |
Если и для любой пары и несмежных вершин графа , то — гамильтонов граф. |
| Теорема (Следствие 2): |
Если и для любой вершины графа , то — гамильтонов граф. |
См. также
Источники информации
- Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 60 с.