Метод Лупанова синтеза схем — различия между версиями
Dimatomp (обсуждение | вклад) (→Доказательство: дописал) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 72 промежуточные версии 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
{{ | {{ | ||
Теорема|statement= | Теорема|statement= | ||
| − | Любая булева функция от < | + | Любая [[Определение булевой функции | булева функция]] от <tex>n</tex> аргументов <tex>f(x_1, x_2, \ldots, x_n)</tex> в базисе <tex>B = \{\neg, \lor, \land\}</tex> имеет [[Реализация булевой функции схемой из функциональных элементов#Схемная сложность | схемную сложность]] <tex>size_B (f) = O\left(\dfrac{2^n}{n}\right)</tex>. |
}} | }} | ||
| + | |||
== Представление функции == | == Представление функции == | ||
| − | + | [[Файл:Lupanov fig1.png|450px|thumb|right|Рис. <tex>1</tex>. Описываемая таблица истинности, разделённая на полосы]] | |
| + | Поделим аргументы функции на два блока: первые <tex>k</tex> и оставшиеся <tex>(n - k)</tex>. | ||
| + | |||
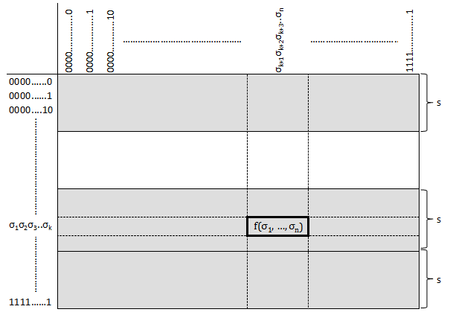
| + | Для удобства дальнейших рассуждений представим булеву функцию в виде таблицы, изображённой на рис. <tex>1</tex>. Строки индексируются значениями первых <tex>k</tex> переменных, столбцы — значениями оставшихся <tex>(n - k)</tex>; таким образом, на пересечении столбца и строки находится значение функции для соответствующего набора аргументов. | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Разделение на полосы == | == Разделение на полосы == | ||
| − | Разделим | + | Разделим таблицу на '''''горизонтальные полосы''''' шириной <tex>s</tex> (последняя полоса, возможно, будет короче остальных; её ширину обозначим <tex>s'</tex>). Пронумеруем полосы сверху вниз от <tex>1</tex> до <tex dpi="145">p=\left\lceil\dfrac{2^k}{s}\right\rceil</tex>. |
| − | Рассмотрим независимо некоторую полосу. | + | Рассмотрим независимо некоторую полосу. Заметим, что среди её столбцов при небольшом <tex>s</tex> будет много повторений; далее про одинаковые столбцы, находящиеся в одной полосе, будем говорить, что они одного '''''сорта'''''. |
{{ | {{ | ||
Определение|definition= | Определение|definition= | ||
| − | '''Сорт''' столбца полосы - класс эквивалентности | + | '''Сорт''' некоторого столбца данной полосы {{---}} его [[Отношение эквивалентности#Классы эквивалентности | класс эквивалентности]] по отношению поэлементного равенства столбцов данной полосы. |
}} | }} | ||
| − | Число сортов столбцов < | + | Число сортов столбцов <tex>i</tex>-й полосы обозначим как <tex>t(i)</tex>. Понятно, что для любой полосы <tex>t(i) \leqslant 2^s</tex> (для последней <tex>t(p) \leqslant 2^{s'}</tex>). |
| − | == Функция для полосы == | + | |
| − | Пусть для некоторого < | + | == Функция для одной полосы == |
| − | * < | + | [[Файл:Lupanov_fig2.png|330px|thumb|right|Рис. <tex>2</tex>. Значения, возвращаемые функцией <tex>g_{ij}</tex>]] |
| − | * < | + | Пусть для некоторого <tex>i</tex> |
| + | * <tex>\beta_{j}</tex> {{---}} произвольный столбец <tex>i</tex>-й полосы <tex>j</tex>-го сорта (точное положение столбца далее не будет иметь значения, по определению сорта) | ||
| + | * <tex>(\sigma_1^l, \sigma_2^l, \ldots, \sigma_k^l)</tex> {{---}} аргументы функции, соответствующие <tex>l</tex>-й строке <tex>i</tex>-й полосы. | ||
Тогда введём булеву функцию | Тогда введём булеву функцию | ||
| − | < | + | <tex>g_{ij}(x_1, x_2, \ldots, x_k) = \begin{cases} |
| − | \beta_{jl} | + | \beta_{jl}, \mbox{ if } \exists l \in [1; s]~(x_1, x_2, \ldots, x_k) = (\sigma_1^l, \sigma_2^l, \ldots, \sigma_k^l) \\ |
| − | 0 | + | 0, \mbox{ otherwise} |
| − | \end{cases}</ | + | \end{cases}</tex> |
| + | |||
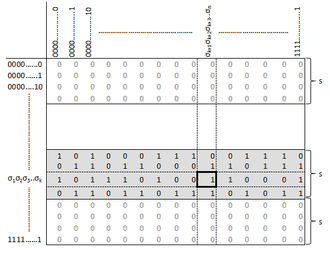
| + | Другими словами, если строка, соответствующая аргументам функции <tex>x_1, x_2, \ldots, x_k</tex>, находится в <tex>i</tex>-й полосе, то функция возвращает значение, записанное в столбце сорта <tex>j</tex> для этой строки. Если же эта строка находится в другой полосе, то функция вернёт <tex>0</tex>. Иллюстрация принципа работы функции <tex>g_{ij}</tex> приведена на рис. <tex>2</tex>. | ||
| + | === Вывод исходной функции для фиксированной части параметров === | ||
| + | Поскольку изначальный столбец <tex>(\sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_{n})</tex> складывается из столбцов соответствующих сортов в полосах, | ||
| + | <tex dpi="145">f(x_1, x_2, \ldots, x_k, \sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_{n}) = \bigvee\limits_{i = 1}^p g_{ij_i}(x_1, x_2, \ldots, x_k)</tex>, | ||
| + | где <tex>j_i</tex> {{---}} номер сорта столбца полосы <tex>i</tex>, являющегося соответствующей частью столбца <tex>(\sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_{n})</tex>. | ||
| − | + | == Мультиплексор и демультиплексор == | |
| − | === | + | {{main|Мультиплексор и демультиплексор}} |
| − | |||
| − | |||
| − | |||
| − | + | Для упрощения доказательства теоремы будем использовать элементы '''''мультиплексор''''' и '''''демультиплексор'''''. | |
| − | Для упрощения доказательства теоремы | ||
{{ | {{ | ||
Определение|definition= | Определение|definition= | ||
| − | '''Мультиплексор''' - логический элемент, получающий на вход | + | '''Мультиплексор''' (''англ.'' multiplexer) {{---}} логический элемент, получающий на вход |
| − | * < | + | * <tex>2^n</tex> булевых значений; |
| − | * < | + | * <tex>n</tex>-значное число <tex>x</tex> в двоичном представлении |
| − | и возвращающий значение на < | + | и возвращающий значение на <tex>x</tex>-м входе. |
}}{{ | }}{{ | ||
Определение|definition= | Определение|definition= | ||
| − | ''' | + | '''Демультиплексор''' (''англ.'' demultiplexer) {{---}} логический элемент, получающий на вход |
| − | * булево значение < | + | * булево значение <tex>z</tex>; |
| − | * < | + | * <tex>n</tex>-значное число <tex>x</tex> в двоичном представлении |
| − | и выводящий < | + | и выводящий <tex>z</tex> на <tex>x</tex>-й из своих <tex>2^n</tex> выходов. На все остальные выходы элемент выдаёт <tex>0</tex>. |
}} | }} | ||
| − | + | {| | |
| + | |[[Файл:Mux_demux.png|500px|thumb|Мультиплексор слева, демультиплексор справа]] | ||
| + | |} | ||
| − | + | Оба элемента представимы схемами с числом элементов <tex>O(2^n)</tex> с помощью базиса <tex>B</tex>. | |
== Доказательство == | == Доказательство == | ||
| − | В качестве доказательства ниже будет предложен вариант такой схемы для произвольной функции < | + | В качестве доказательства ниже будет предложен вариант такой схемы для произвольной функции <tex>f(x_1, x_2, \ldots, x_n)</tex> (представление Лупанова, ''англ.'' Lupanov <tex>(k, s)</tex>-representation). |
| − | + | [[Файл:Lupanov_scheme.png|550px|Иллюстрация частного случая представления Лупанова, описанного здесь]] | |
| − | + | Для удобства поделим схему на блоки: | |
| − | * '''Блок B''' - схемная реализация всех < | + | * '''Блок A''' {{---}} демультиплексор, которому на вход подали <tex>1</tex> и <tex>(x_1, x_2, \ldots, x_k)</tex> в качестве двоичного представления числа. |
| + | * '''Блок B''' {{---}} схемная реализация всех <tex>g_{ij}</tex>. Функцию <tex>g_{ij}</tex> можно реализовать как <tex dpi="145">\bigvee\limits_{\beta_l = 1} y_{il}</tex>, где <tex>y_{il}</tex> {{---}} выдал ли демультиплексор <tex>1</tex> на <tex>l</tex>-м выходе <tex>i</tex>-й полосы. | ||
| + | * '''Блок C''' {{---}} схемная реализация всех <tex>f(x_1, x_2, \ldots, x_k, \sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_n)</tex>. ''(здесь <tex>\sigma_i</tex> - фиксированные параметры, см. п. <tex>3.1</tex>)'' | ||
| + | * '''Блок D''' {{---}} мультиплексор, получающий на вход все <tex>f(x_1, x_2, \ldots, x_k, \sigma_{k + 1}, \sigma_{k + 2}, \ldots, \sigma_n)</tex> и параметры функции <tex>x_{k + 1}, x_{k + 2}, \ldots, x_n</tex> в качестве двоичного представления числа. '''''Результат работы схемы''''' {{---}} вывод мультиплексора. | ||
| − | + | Положим <tex>s = \lfloor n - 2\log_2 n\rfloor</tex>; <tex>k = \lfloor\log_2 n\rfloor</tex>. Тогда число элементов в блоках | |
| − | * | + | * <tex>L_A = O(2^k) = O(2^{\log_2 n}) = O(n)</tex> |
| + | * <tex>L_B \leqslant (s - 1) \cdot (t(1) + t(2) + \ldots + t(p)) < sp \cdot 2^s = n \cdot \dfrac{2^n}{n^2} = \dfrac{2^n}{n}</tex> | ||
| + | * <tex>L_C = O(p \cdot 2^{n - k}) = O\left(\dfrac{p}{n} \cdot 2^n\right) = O\left(\dfrac{2^n}{s}\right) = O\left(\dfrac{2^n}{n - 2\log_2 n}\right)</tex> | ||
| + | * <tex>L_D = O(2^{n - k}) = O\left(\dfrac{2^n}{n}\right)</tex> | ||
| − | + | Итого, имеем схему c числом элементов <tex>L_A + L_B + L_C + L_D = O(n) + O\left(\frac{2^n}{n}\right) + O\left(\dfrac{2^n}{n - 2\log_2 n}\right) + O\left(\dfrac{2^n}{n}\right) = O\left(\dfrac{2^n}{n}\right)</tex>, откуда следует, что <tex>size_B (f) = O\left(\dfrac{2^n}{n}\right)</tex>, что и требовалось доказать. | |
| − | |||
| − | + | == См. также == | |
| + | *[[Реализация_булевой_функции_схемой_из_функциональных_элементов|Реализация булевой функции схемой из функциональных элементов]] | ||
| + | *[[Простейшие_методы_синтеза_схем_из_функциональных_элементов|Простейшие методы синтеза схем из функциональных элементов]] | ||
| + | *[[Контактная_схема|Контактная схема]] | ||
| − | |||
| − | + | == Источник информации == | |
| − | * | + | * Яблонский С.В. Введение в дискретную математику {{---}} М.:"Наука", 1986 {{---}} стр. 361 |
| − | + | * [http://en.wikipedia.org/wiki/Multiplexer Wikipedia {{---}} Multiplexer] | |
| − | * | ||
| − | |||
| − | + | [[Категория:Дискретная математика и алгоритмы]] | |
| + | [[Категория: Схемы из функциональных элементов ]] | ||
Текущая версия на 19:13, 4 сентября 2022
| Теорема: |
Любая булева функция от аргументов в базисе имеет схемную сложность . |
Содержание
Представление функции
Поделим аргументы функции на два блока: первые и оставшиеся .
Для удобства дальнейших рассуждений представим булеву функцию в виде таблицы, изображённой на рис. . Строки индексируются значениями первых переменных, столбцы — значениями оставшихся ; таким образом, на пересечении столбца и строки находится значение функции для соответствующего набора аргументов.
Разделение на полосы
Разделим таблицу на горизонтальные полосы шириной (последняя полоса, возможно, будет короче остальных; её ширину обозначим ). Пронумеруем полосы сверху вниз от до .
Рассмотрим независимо некоторую полосу. Заметим, что среди её столбцов при небольшом будет много повторений; далее про одинаковые столбцы, находящиеся в одной полосе, будем говорить, что они одного сорта.
| Определение: |
| Сорт некоторого столбца данной полосы — его класс эквивалентности по отношению поэлементного равенства столбцов данной полосы. |
Число сортов столбцов -й полосы обозначим как . Понятно, что для любой полосы (для последней ).
Функция для одной полосы
Пусть для некоторого
- — произвольный столбец -й полосы -го сорта (точное положение столбца далее не будет иметь значения, по определению сорта)
- — аргументы функции, соответствующие -й строке -й полосы.
Тогда введём булеву функцию
Другими словами, если строка, соответствующая аргументам функции , находится в -й полосе, то функция возвращает значение, записанное в столбце сорта для этой строки. Если же эта строка находится в другой полосе, то функция вернёт . Иллюстрация принципа работы функции приведена на рис. .
Вывод исходной функции для фиксированной части параметров
Поскольку изначальный столбец складывается из столбцов соответствующих сортов в полосах, , где — номер сорта столбца полосы , являющегося соответствующей частью столбца .
Мультиплексор и демультиплексор
Для упрощения доказательства теоремы будем использовать элементы мультиплексор и демультиплексор.
| Определение: |
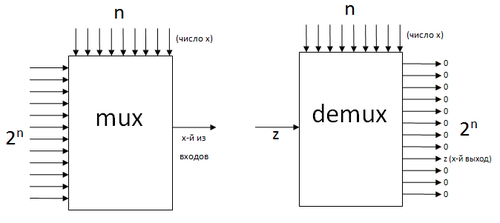
Мультиплексор (англ. multiplexer) — логический элемент, получающий на вход
|
| Определение: |
Демультиплексор (англ. demultiplexer) — логический элемент, получающий на вход
|
Оба элемента представимы схемами с числом элементов с помощью базиса .
Доказательство
В качестве доказательства ниже будет предложен вариант такой схемы для произвольной функции (представление Лупанова, англ. Lupanov -representation).
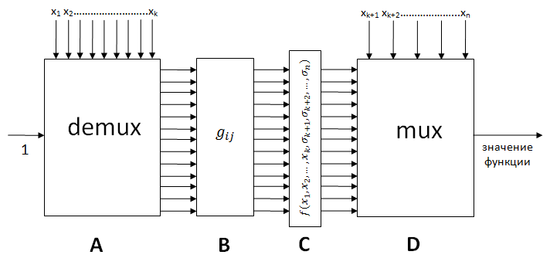
Для удобства поделим схему на блоки:
- Блок A — демультиплексор, которому на вход подали и в качестве двоичного представления числа.
- Блок B — схемная реализация всех . Функцию можно реализовать как , где — выдал ли демультиплексор на -м выходе -й полосы.
- Блок C — схемная реализация всех . (здесь - фиксированные параметры, см. п. )
- Блок D — мультиплексор, получающий на вход все и параметры функции в качестве двоичного представления числа. Результат работы схемы — вывод мультиплексора.
Положим ; . Тогда число элементов в блоках
Итого, имеем схему c числом элементов , откуда следует, что , что и требовалось доказать.
См. также
- Реализация булевой функции схемой из функциональных элементов
- Простейшие методы синтеза схем из функциональных элементов
- Контактная схема
Источник информации
- Яблонский С.В. Введение в дискретную математику — М.:"Наука", 1986 — стр. 361
- Wikipedia — Multiplexer