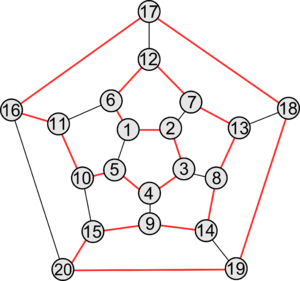
Гамильтоновы графы
Основные определения
| Определение: |
| Гамильтоновым путём (англ. Hamiltonian path) называется простой путь, проходящий через каждую вершину графа ровно один раз. |
| Определение: |
| Гамильтоновым циклом (англ. Hamiltonian cycle) называют замкнутый гамильтонов путь. |
| Определение: |
| Граф называется полугамильтоновым (англ. Semihamiltonian graph), если он содержит гамильтонов путь. |
| Определение: |
| Граф называется гамильтоновым (англ. Hamiltonian graph), если он содержит гамильтонов цикл. |
Очевидно, что любой гамильтонов граф также и полугамильтонов.
Достаточные условия гамильтоновости графа
Теорема Дирака
| Теорема: |
Если и для любой вершины неориентированного графа , то — гамильтонов граф. |
Теорема Оре
| Теорема: |
Если и для любых двух различных несмежных вершин и неориентированного графа , то — гамильтонов граф. |
Теорема Поша
| Теорема (Поша): |
Пусть граф имеет вершин и выполнены следующие два условия:
|
Теорема Редеи-Камиона
| Теорема: |
Любой сильносвязный турнир — гамильтонов. |
Теорема Гуйя-Ури
| Теорема (Ghouila-Houri): |
Пусть — сильносвязный ориентированный граф. — гамильтонов. |
Теорема Хватала
| Теорема (Хватал): |
Пусть:
Тогда если верна импликация: |
Задача о коммивояжере
Рассмотрим алгоритм нахождения гамильтонова цикла на примере задачи о коммивояжёре.
Описание задачи
| Задача: |
| Задача о коммивояжере (англ. Travelling salesman problem, TSP) — задача, в которой коммивояжер должен посетить городов, побывав в каждом из них ровно по одному разу и завершив путешествие в том городе, с которого он начал. В какой последовательности ему нужно обходить города, чтобы общая длина его пути была наименьшей? |
Варианты решения
Задача о коммивояжере относится к классу NP-полных задач. Рассмотрим два варианта решения с экспоненциальным временем работы.
Перебор перестановок
Можно решить задачу перебором всевозможных перестановок. Для этого нужно сгенерировать все всевозможных перестановок вершин исходного графа, подсчитать для каждой перестановки длину маршрута и выбрать минимальный из них. Но тогда задача оказывается неосуществимой даже для достаточно небольших . Сложность алгоритма .
Динамическое программирование по подмножествам (по маскам)
Задача о коммивояжере представляет собой поиск кратчайшего гамильтонова цикла в графе. Зафиксируем начальную вершину и будем искать гамильтонов цикл наименьшей стоимости — путь от до , проходящий по всем вершинам (кроме первоначальной) один раз. Т.к. искомый цикл проходит через каждую вершину, то выбор не имеет значения. Поэтому будем считать .
Подмножества вершин будем кодировать битовыми векторами, обозначим значение -ого бита в векторе .
Обозначим как наименьшую стоимость пути из вершины в вершину , проходящую (не считая вершины ) единожды по всем тем и только тем вершинам , для которых (т.е. уже найденный оптимальный путь от -ой вершины до -ой, проходящий через те вершины, где . Если ,то эти вершины еще не посещены).
Алгоритм поиска цикла будет выглядеть следующим образом:
- Начальное состояние — когда находимся в -й вершине, ни одна вершина не посещена, а пройденный путь равен (т.е. и ).
- Для остальных состояний ( или ) перебираем все возможные переходы в -ую вершину из любой посещенной ранее и выбираем минимальный результат.
- Если возможные переходы отсутствуют, решения для данной подзадачи не существует (обозначим ответ для такой подзадачи как ).
Стоимостью минимального гамильтонова цикла в исходном графе будет значение — стоимость пути из -й вершины в -ю, при необходимости посетить все вершины. Данное решение требует памяти и времени.
Для того, чтобы восстановить сам путь, воспользуемся соотношением , которое выполняется для всех ребер, входящих в минимальный цикл . Начнем с состояния , , найдем вершину , для которой выполняется указанное соотношение, добавим в ответ, пересчитаем текущее состояние как , . Процесс заканчивается в состоянии , .
Оптимизация решения методом динамического программирования
Пусть содержит булево значение — существует ли в подмножестве гамильтонов путь, заканчивающийся в вершине .
Сама динамика будет такая:
Это решение требует памяти и времени. Эту оценку можно улучшить, если изменить динамику следующим образом.
Пусть теперь хранит маску подмножества всех вершин, для которых существует гамильтонов путь в подмножестве , заканчивающихся в этой вершине. Другими словами, сожмем предыдущую динамику: будет равно . Для графа выпишем масок , для каждой вершины задающие множество вершин, которые связаны ребром с данной вершиной. То есть .
Тогда динамика перепишется следующим образом:
Особое внимание следует уделить выражению . Первая часть выражения содержит подмножество вершин, для которых существует гамильтонов путь, заканчивающихся в соответствующих вершинах в подмножестве без вершины , а вторая — подмножество вершин, связанных с ребром. Если эти множества пересекаются хотя бы по одной вершине (их не равен ), то, как нетрудно понять, в существует гамильтонов путь, заканчивающийся в вершине .
Окончательная проверка состоит в сравнении c .
Это решение использует памяти и имеет асимптотику .
Псевдокод
Прежде чем писать код, скажем пару слов о порядке обхода состояний. Обозначим за количество единиц в маске (иначе говоря количество пройденных вершин не считая текущей). Тогда, поскольку при рассмотрении состояния мы смотрим на состояния
, и , то состояния с большим должны быть посещены позже, чтобы к моменту вычисления текущего состояния были вычислены все те, которые используются для его подсчёта. Однако если использовать рекурсию, об этом можно не беспокоиться (и сэкономить немало кода, времени и памяти).
// все переменные используются из описания алгоритма, = бесконечность function findCheapest(i, mask): if d[i][mask] != return d[i][mask] for j = 0 .. n - 1 if w(i, j) существует and j-ый бит mask == 1 d[i][mask] = min(d[i][mask], findCheapest(j, mask - ) + w(i, j)) return d[i][mask] function start(): for i = 0 .. n - 1 for mask = 0 .. - 1 d[i][mask] = d[0][0] = 0 ans = findCheapest(0, - 1) return ans
Дальше ищем сам цикл:
function findWay(): i = 0 mask = - 1 path.push(0) while mask != 0 for j = 0 .. n - 1 if w(i, j) существует and j-ый бит mask == 1 and d[i][mask] == d[j][mask - ] + w(i, j) path.push(j) i = j mask = mask - continue
Алгоритм нахождения гамильтонова цикла
Алгоритм нахождения гамильтонова цикла легко получить слегка изменив алгоритм нахождения минимального гамильтонова цикла. В массиве мы хранили расстояния, но сейчас нас не интересует какой длины будет это расстояние, так как главной задачей является нахождение цикла. В этом массиве мы теперь просто храним посещение вершин. И каждый раз, когда при запуске находим непосещенную вершину, то запускаем функцию рекурсивно от нее. Если она возвращает , то есть до вершины можно добраться, то записываем, что мы можем посетить вершину. Проходы так же осуществляются по рёбрам.
Алгоритм нахождения гамильтонова пути
Алгоритм нахождения гамильтонова пути легко получить, используя алгоритм нахождения гамильтонова цикла. Нужно добавить в граф еще одну вершину и ребра от нее до всех остальных вершин и из всех остальных вершин до неё. И далее запустить алгоритм поиска цикла от новой вершины. В восстановлении пути учтем, что эта вершина лишняя, и не будем записывать её в путь.
См. также
Источники информации
- Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 60 с.
- Седжвик Р. Фундаментальные алгоритмы на C++. Алгоритмы на графах. — СПб: ООО «ДиаСофтЮП», 2002.
- Гамильтонов граф
- Задача коммивояжера в русской википедии
- Задача коммивояжера в немецкой википедии
- Романовский И. В. Дискретный анализ. СПб.: Невский Диалект; БХВ-Петербург, 2003. ISBN 5-7940-0114-3
- Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, 2-е издание. М.: Издательский дом "Вильямс", 2005. ISBN 5-8459-0857-4