Динамическое программирование

<wikitex> Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А.Кумок

Процесс разработки алгоритмов динамического программирования

В процессе составления алгоритмов динамического программирования, требуется следовать последовательности из четырёх действий:

1. Описать структуру оптимального решения.
2. Рекурсивно определить значение оптимального решения.
3. Вычислить значение оптимального решения с помощью метода восходящего анализа.
4. Составить оптимальное решение на основе полученной информации.

Оптимальная подструктура

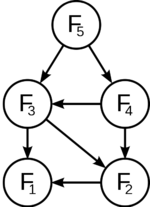
Задача имеет оптимальную подструктуру, если её оптимальное решение может быть рационально составлено из оптимальных решений её подзадач.

Граф подзадач для чисел Фибоначчи

Наличие оптимальной подструктуры в задаче используется для определения применимости динамического программирования и жадных алгоритмов для решения оной. Например, задача по нахождению кратчайшего пути между некоторыми вершинами графа содержит в себе оптимальное решение подзадач.

Многие задачи, решаемые динамическим программированием, можно определить как поиск в заданном ориентированном ациклическом графе кратчайшего пути от одной вершины к другой.

Задача о самом длинном невзвешенном пути

Отсутствие оптимальной подструктуры

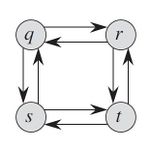
Иногда оптимальная подструктура может отсутствовать в задаче. Рассмотрим задачу, в которой имеется ориентированный граф $G = (V, E)$ и вершины $u, v \in V$, задачу по определению простого пути от вершины $u$ к вершине $v$, состоящий из максимального количества рёбер.

Рассмотрим путь $q \rightarrow r \rightarrow t$, который является самым длинным простым путем $q \rightsquigarrow t$. Является ли путь $q \rightarrow r$ самым длинным путем $q \rightsquigarrow r$? Нет, поскольку простой путь $q \rightarrow s \rightarrow t \rightarrow r$ длиннее. Является ли путь $r \rightarrow t$ самым длинным путем $r \rightsquigarrow t$? Снова нет, поскольку простой путь $r \rightarrow q \rightarrow s \rightarrow t$ длиннее. Таким образом, в задаче о поиске самого длинного невзвешенного пути не возникает никаких оптимальных подструктур. Для этой задачи до сих пор не найдено ни одного эффективного алгоритма, работающего по принципу динамического программирования. Фактически, это NP-полная задача, т.е. вряд ли ее можно решить в течение полиномиального времени.

Оптимальность для подзадач

Важнейшее свойство задач, которое позволяет решать их с помощью динамического программирования, это оптимальность для подзадач. В зависимости от формулировки задачи, будь то динамическое программирование на отрезке, на префиксе, на дереве, термин оптимальности для подзадач может быть различным, но, в целом, формулируется так: если есть оптимальное решение для некоторой подзадачи, которая возникает в процессе решения задачи, то именно его нужно использовать для решения задачи в целом.

Принцип оптимальности на префиксе

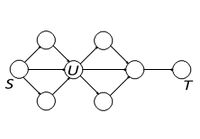
Рассмотрим некий необратимый процесс производства и представим его в виде ориентированного и ациклического графа. Процесс проходит некий ряд состояний. Началом производства (первым состоянием) обозначим вершину графа $S$, а конец производства (последнее состояние) $T$. Процесс требует оптимизации, т.е. требуется найти оптимальный путь $S \rightsquigarrow T$. Он проходит через вершину графа $U$. Префикс оптимального пути $S \rightsquigarrow U$ является оптимальным путём $S \rightsquigarrow U$. Теперь рассмотрим принцип оптимальности для динамического программирования на префиксе. Итак, имеем некоторый оптимальный путь $S \rightsquigarrow T$, который проходит через $U$. Пусть префикс $ \Delta U$, т.е. путь от $S \rightsquigarrow U$, неоптимален. Тогда заменим неоптимальную часть $S \rightsquigarrow U$ пути $S \rightsquigarrow T$ оптимальной, а путь $U \rightsquigarrow T$ добавим в конец. Получим оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется. Т.е. чтобы получить оптимальный путь из одной вершины графа в другую, префиксы меньших путей должны быть оптимальными.

В качестве примера рассмотрим следующую задачу: пусть дан ациклический ориентированный взвешенный граф, требуется найти вес кратчайшего пути из u в v. Воспользуемся принципом оптимальности на префиксе.
Пусть [math]d[/math] — функция, где [math]d(i)[/math] — вес кратчайшего пути из [math]u[/math] в [math]i[/math]. Ясно, что [math]d(u)[/math] равен [math]0[/math]. Пусть [math]w(i, j)[/math] — вес ребра из [math]i[/math] в [math]j[/math]. Будем обходить граф в порядке топологической сортировки. Получаем следующие соотношения:

[math] d(i) = \min\limits_{\mathop{j:j \rightsquigarrow i}} (d(j) + w(j, i)) [/math]

Так как мы обходим граф в порядке топологической сортировки, то на [math]i[/math]-ом шаге всем [math]d(j)[/math] ([math]j[/math] такие, что существует ребро из [math]j[/math] в [math]i[/math]) уже присвоены оптимальные ответы, и, следовательно, [math]d(i)[/math] также будет присвоен оптимальный ответ.

Примеры задач

• Кратчайший путь в ациклическом графе
• Задача о числе путей в ациклическом графе

Принцип оптимальности на подотрезках

Требуется посчитать функцию $f(1, n)$. Принцип состоит в следующем: пусть для всех отрезков $i$, $j$ (где [math] u \leqslant i \leqslant j \leqslant v [/math]) известен оптимальный ответ для функции $f(i, j)$. Тогда мы будем вычислять $f(u, v)$ через такие $f(i, j)$. В качестве примера рассмотрим следующую классическую задачу: дана строка длины n, нужно найти максимальный подпалиндром (подпоследовательность максимальной длины, которая является палиндромом). Пусть $d(i, j)$ - ответ на задачу для подстроки, начинающаяся с символа $i$ и заканчивающаяся в символе $j$. Ясно, что $d(i, j) = 0$ для всех $i, j,$ таких что $i > j$ и $d(i, i) = 1$ для всех $i$. Пусть нам нужно посчитать значение для $d(i, j)$, причем значение $d$ для всех $l, r$, таких что [math] i \leqslant l \leqslant r \leqslant j [/math] уже посчитаны и они оптимальны. Рассмотрим два случая:

1. [math] s(i) \neq s(j), тогда d(i, j) = \max(d(i, j - 1), d(i + 1, j)) [/math]
   
2. [math] s(i) = s(j), тогда d(i, j) = d(i + 1, j - 1) + 2 [/math]
   

Доказательство:

1. Так [math]s(i) \neq s(j)[/math], символы $s(i)$ и $s(j)$ не могут входить в максимальный подпалиндром одновременно, то есть либо $s(i)$ входят в максимальный подпалиндром(тогда его длина $d[i, j - 1]$), либо $s(j)$ входит в максимальный подпалиндром (тогда его длина $d[i + 1, j]$), либо оба не входят в максимальный подпалиндром (тогда его длина $= d[i, j - 1] = d[i + 1, j]$).
   
2. Данное равенство следует из факта, что выгодно включить в максимальный подпалиндром символы $s(i)$ и $s(j)$.

Примеры задач

• Задача о расстановке знаков в выражении
• Задача о порядке перемножения матриц
• Задача о выводе в контекстно-свободной грамматике, алгоритм Кока-Янгера-Касами
• Задача об оптимальном префиксном коде с сохранением порядка. Монотонность точки разреза
• Задача о наибольшей общей подпоследовательности
• Задача о редакционном расстоянии, алгоритм Вагнера-Фишера
• Задача о расстоянии Дамерау-Левенштейна
• Задача о наибольшей общей подпоследовательности

Принцип оптимальности на подмножествах

Требуется посчитать функцию [math]f(A)[/math], где [math]A[/math] — некоторое множество. Принцип состоит в следующем: пусть для всех множеств [math]B[/math] (где [math]B \in A[/math]) известен оптимальный ответ для функции [math]f(B)[/math]. Тогда будем вычислять [math]f(A)[/math] через такие [math]f(B)[/math]. В качестве примера рассмотрим задачу о коммивояжере.

Обозначим [math]d[i][mask][/math] как наименьшую стоимость пути из вершины [math]i[/math] в вершину [math]0[/math], проходящую (не считая вершины [math]i[/math]) единожды по всем тем и только тем вершинам [math]j[/math], для которых [math]mask_j = 1[/math] (т.е. [math]d[i][mask][/math] уже найденный оптимальный путь от [math]i[/math]-ой вершины до [math]0[/math]-ой, проходящий через те вершины, где [math]mask_j=1[/math]. Если [math]mask_j=0[/math],то эти вершины еще не посещены). Тогда воспользуемся принципом оптимальности на подмножествах. Стоимостью минимального гамильтонова цикла в исходном графе будет значение [math] d[0][2^n-1][/math] — стоимость пути из [math]0[/math]-й вершины в [math]0[/math]-ю, при необходимости посетить все вершины.

Примеры задач

• Задача коммивояжера, ДП по подмножествам

Мемоизация

Определение:

Мемоизация (англ. memoization) — сохранение результатов выполнения функций для предотвращения повторных вычислений.

Это один из способов оптимизации, применяемый для увеличения скорости выполнения компьютерных программ. Перед вызовом функции проверяется, вызывалась ли функция ранее:

• если не вызывалась, функция вызывается и результат её выполнения сохраняется;
• если вызывалась, используется сохранённый результат.

В качестве примера рассмотрим задачу о нахождении числа Фибоначчи под номером [math]n[/math]. Без мемоизации:

int Fibonacci(int n): 
  if n <= 1
    return 1
  a = Fibonacci(n - 1)
  b = Fibonacci(n - 2)
  return a + b

С мемоизацией:

int Fibonacci(int n): 
  if n <= 1
    return 1
  if fib[n] != -1 // проверка на то, не посчитали ли мы это число раньше; посчитанные числа хранятся в массиве fib
    return fib[n]
  fib[n - 1] = Fibonacci(n - 1)
  fib[n - 2] = Fibonacci(n - 2)
  return fib[n - 1] + fib[n - 2]

См.также

• Динамическое программирование по профилю
• Динамика по поддеревьям

Источники информации

• Т. Кормен. «Алгоритмы. Построение и анализ» второе издание, Глава 15
• T. H. Cormen. «Introduction to Algorithms» third edition, Chapter 15
• Wikipedia — Optimal substructure
• Wikipedia — Greedy algorithm
• Wikipedia — Dynamic programming
• Wikipedia — Memoization
• Википедия — Жадный алгоритм
• Википедия — Динамическое программирование
• Википедия — Мемоизация

</wikitex>